Оглавление:
Определение динамических реакций опор вращающегося тела
При вращении твердого тела вокруг неподвижной оси силы давления на его опоры (подшипники и подпятники) могут, вообще говоря, значительно отличаться от тех сил давления, которые испытывают опоры при отсутствии вращения тела.
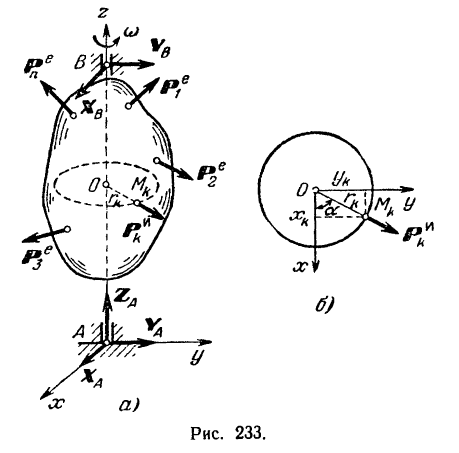
Пусть какое-либо твердое тело под действием приложенных к нему внешних заданных сил
равномерно вращается вокруг неподвижной оси  , закрепленной в подпятнике
, закрепленной в подпятнике  и подшипнике
и подшипнике 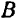 (рис. 233, а).
(рис. 233, а).
Освободив мысленно тело от связей, заменим действие на него подпятника 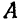 и подшипника
и подшипника 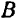 их реакциями. Разложим эти реакции на составляющие
их реакциями. Разложим эти реакции на составляющие 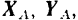
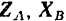 и
и 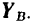
Реакции опор, возникающие при вращении тела, называются динамическими. Для их определения воспользуемся методом кинетостатики.
Условно приложим ко всем материальным частицам тела силы инерции этих частиц. Во всякий момент вращения тела приложенные к нему внешние силы, силы реакции связей и силы инерции всех частиц тела удовлетворяют условиям равновесия и потому к ним можно применить известные из статики (§ 36) шесть уравнений равновесия произвольной пространственной системы сил:
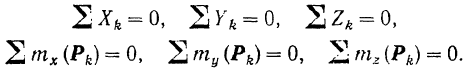
В данном случае эти уравнения принимают вид:
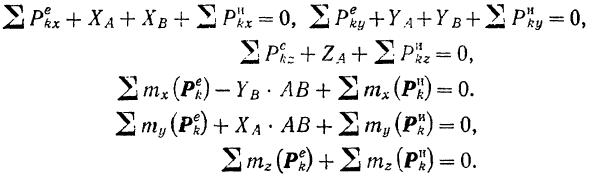
Вычислим сначала суммы проекций сил инерции всех точек тела на каждую из трех координатных осей и суммы моментов этих сил относительно тех же осей.
Разложим силу 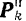 инерции каждой
инерции каждой 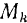 точки тела (рис. 233, а) на тангенциальную
точки тела (рис. 233, а) на тангенциальную 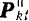 силу инерции и нормальную
силу инерции и нормальную 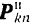 силу инерции.
силу инерции.
Так как тело вращается равномерно, то 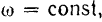
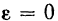 и
и 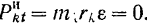 . Нормальная сила инерции
. Нормальная сила инерции 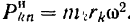 Таким образом, полная сила инерции точки
Таким образом, полная сила инерции точки
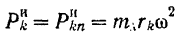
и направлена по соответствующему радиусу от центра.
Проектируя силу инерции каждой точки 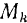 тела на координатные оси (рис. 233, б) и пользуясь равенствами
тела на координатные оси (рис. 233, б) и пользуясь равенствами
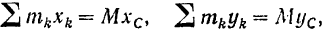
полученными из формул (138) для координат центра масс, найдем:
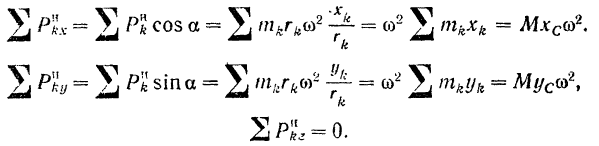
Для вычисления сумм моментов сил инерции относительно координатных осей воспользуемся формулами (36):
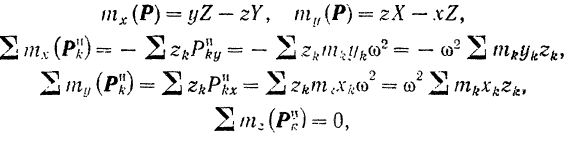
так как линия действия 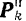 пересекает ось
пересекает ось 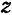 .
.
Сумма, составленная из произведений массы каждой материальной частицы тела на две координаты этой частицы в какой-либо прямоугольной системе координатных осей, называется центробежным моментом инерции тела относительно двух соответствующих осей. Обозначая соответственно
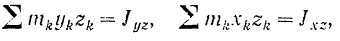
будем иметь:
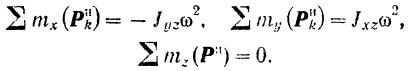
Подставляя найденные выражения для составляющих сил инерции и моментов этих сил в уравнения равновесия тела, окончательно получим:
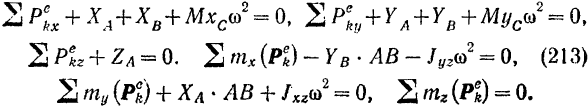
Последнее из полученных уравнений удовлетворяется тождественно. При 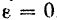 , согласно равенству (182)
, согласно равенству (182)
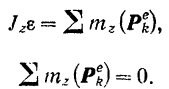
Третье из этих уравнений
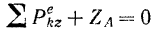
позволяет сразу определить составляющую реакции подпятника, направленную вдоль оси вращения. Как видно из уравнения, эта составляющая не зависит от угловой скорости 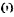 .
.
Первое, второе, четвертое и пятое из уравнений (213) служат для определения динамических реакций опор, лежащих в плоскости, перпендикулярной оси вращения тела. Как видно из этих уравнений, они зависят не только от внешних заданных сил, но еще и от угловой скорости вращения тела.
Полагая в этих уравнениях 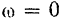 , мы получим уравнения для определения составляющих статических реакций опор, которые действовали бы па ось вращения в том случае, если бы под действием тех же самых заданных внешних сил тело находилось в покое.
, мы получим уравнения для определения составляющих статических реакций опор, которые действовали бы па ось вращения в том случае, если бы под действием тех же самых заданных внешних сил тело находилось в покое.
При вращении тела динамические составляющие реакций опор могут быть значительно больше статических. Они зависят, очевидно, от величии 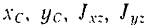 особенно от величины угловой скорости
особенно от величины угловой скорости 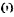 тела. В современной технике угловые скорости вращающихся тел могут быть весьма большими и потому определение динамических реакций опор таких тел является важной инженерной задачей.
тела. В современной технике угловые скорости вращающихся тел могут быть весьма большими и потому определение динамических реакций опор таких тел является важной инженерной задачей.
Из уравнения (213) видно, что реакции опор не будут зависеть от угловой скорости вращения тела, если будут соблюдены следующие условия:
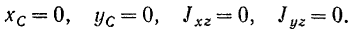
Проходящая через центр тяжести тела ось 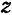 , для которой центробежные моменты инерции
, для которой центробежные моменты инерции 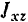 и
и 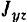 , содержащие в своих индексах наименование данной оси, равны пулю, называется гласной центральной осью инерции гола.
, содержащие в своих индексах наименование данной оси, равны пулю, называется гласной центральной осью инерции гола.
Вращающееся тело, реакции опор которого не от величины угловой скорости и углового ускорения гола, называется динамически уравновешенным.
Равенства (214) выражают, таким образом, следующее условие: для того чтобы вращающееся тело было динамически уравновешенным, его ось вращения должна быть одной из главных центральных осей инерции тела.
Для упрощения вывода нами был рассмотрен случай равномерного вращения тела, но установленные условия (214) динамической уравновешенности остаются справедливыми и при неравномерном вращении тела.
Если тело имеет ось симметрии, то эта ось будет одной из главных центральных осей инерции тела, так как для нее удовлетворяются условия (214).
Чаше всего вращающимся деталям машин и придают форму тел вращения, с тем чтобы они вращались вокруг своих осей симметрии. Если же из-за неизбежных погрешностей изготовления ось вращения тела не будет точно совпадать с его осью симметрии или если ось вращения тела не является его осью симметрии по характеру конструкции (например, коленчатого вала), то специальными приемами (динамической балансировкой тела) добиваются совпадения оси вращения тела с сто главной центральной осью инерции. В основе динамической балансировки тела лежит то положение, что прибавлением (или удалением) двух точечных масс, лежащих в произвольно выбранных плоскостях, перпендикулярных к оси вращения тела, последнюю всегда мох но сделать главной центральной осью инерции тела.
Выбор величины 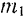 и
и 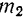 этих масс, а также их координат
этих масс, а также их координат 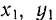 в плоскости
в плоскости 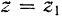 , и
, и 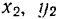 в плоскости
в плоскости 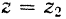 производится с помощью уравнений:
производится с помощью уравнений:
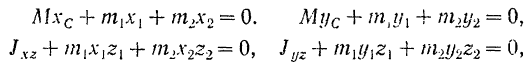
где 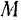 — масса тела,
— масса тела, 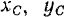 — координаты его центра масс,
— координаты его центра масс, 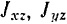 — центробежные моменты инерции тела, вычисленные до присоединения к телу масс
— центробежные моменты инерции тела, вычисленные до присоединения к телу масс 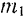 и
и 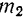 .
.
Для определения шести неизвестных величин из четырех последних уравнений двумя из них, например 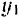 и
и 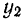 или
или 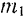 и
и 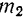 , нужно, конечно, задаться.
, нужно, конечно, задаться.
При определении динамических реакций опор обычно бывает удобней составлять с помощью метода кинетостатики уравнения равновесия для каждого конкретного случая, а не пользоваться готовыми уравнениями (213).
Пример задачи:
Крестовика 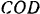 (рис. 234), на концах которой находятся точечные грузы
(рис. 234), на концах которой находятся точечные грузы 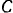 и
и 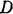 равного веса
равного веса 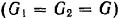 , равномерно вращается вокруг вертикальной оси
, равномерно вращается вокруг вертикальной оси 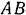 . проходящей через середину длины крестовины. Пренебрегая весом крестовины, определить реакции подпятника
. проходящей через середину длины крестовины. Пренебрегая весом крестовины, определить реакции подпятника 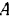 и цилиндрического подшипника
и цилиндрического подшипника 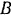 в тот момент, когда крестовина
в тот момент, когда крестовина 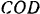 находится в плоскости
находится в плоскости 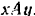 . Известны расстояния:
. Известны расстояния: 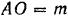
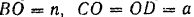 и жесткий угол
и жесткий угол 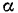 между крестовиной и осью вращения
между крестовиной и осью вращения 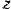 .
.
Решение:
Пользуясь методом кинетостатики, условно присоединим к силам, действующим на крестовину, силы инерции точечных грузов 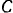 и
и 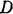 . Так как крестовина вращается равномерно
. Так как крестовина вращается равномерно 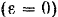 , то касательные составляющие сил инерции грузов равны нулю. Центробежные силы инерции грузов равны по модулю
, то касательные составляющие сил инерции грузов равны нулю. Центробежные силы инерции грузов равны по модулю
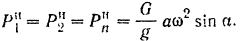
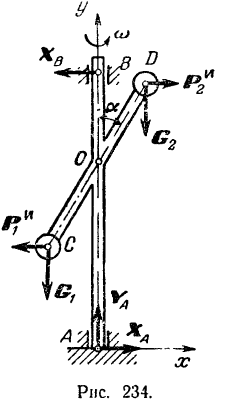
В момент, когда крестовина находится в плоскости 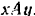 , действующие на нее активные силы
, действующие на нее активные силы 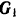 и
и 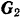 и центробежные силы инерции грузов лежат в той же плоскости. Следовательно, в этой же плоскости будут лежать и реакции связей. Неизвестную по направлению реакцию подпятника раскладываем на составляющие
и центробежные силы инерции грузов лежат в той же плоскости. Следовательно, в этой же плоскости будут лежать и реакции связей. Неизвестную по направлению реакцию подпятника раскладываем на составляющие 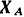 и
и 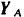 . Реакция
. Реакция 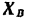 подшипника перпендикулярна к его осн.
подшипника перпендикулярна к его осн.
Составляем уравнения равновесия плоской системы сил
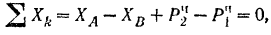
откуда
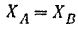
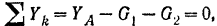
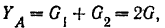
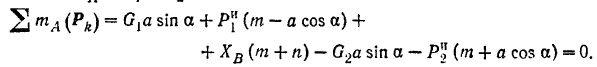
Из последнего уравнения находим:
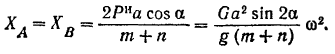
Если бы крестовина ее вращалась, то горизонтальные реакции связен 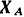 и
и 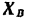 равнялись бы нулю, и следовательно, подшипник и подпятник не испытывали бы боковых давлений. При вращении же крестовины эти реакции (а следовательно, и боковые давления на связи) пропорциональны квадрату угловой скорости крестовины и могут достигать весьма большой величины. При вращении крестовины возникающие динамические реакции вызывают биение вала в подшипниках и усиленный их износ.
равнялись бы нулю, и следовательно, подшипник и подпятник не испытывали бы боковых давлений. При вращении же крестовины эти реакции (а следовательно, и боковые давления на связи) пропорциональны квадрату угловой скорости крестовины и могут достигать весьма большой величины. При вращении крестовины возникающие динамические реакции вызывают биение вала в подшипниках и усиленный их износ.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

