Оглавление:



Определение деформаций при косом изгибе.
- Определение деформации при косом изгибе. Для определения прогиба различных участков балки при косом изгибе вновь применяют метод приложения действия сил. Возвращаясь к примеру, описанному в предыдущем абзаце, находим отклонение первой точки B (свободного конца балки) только от действия силы Pz, это
отклонение f z аналогично одной точке D o t отклонение одной силы вдоль оси Z, направленной вдоль оси y и уравнение g _ Ru/8__ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ZET; — 3Z CP Полное отклонение конца балки f является геометрическим (рис. 414) сумма обоих этих отклонений; она равна Но Ноль. Но — Р Зет Фигура. Четыреста четырнадцать В то же время Пон! = тг е з потому что СР ЮЖД И Дж грех Ф з
потому что* (26.9)) (26.10)) Угол, образованный суммарным отклонением Людмила Фирмаль
f от оси g, равен углу a, т. е. отклонение f направлено перпендикулярно нейтральной оси. Изгиб балки происходит не на плоскости действия внешней силы, а на плоскости, перпендикулярной нейтральной оси(рис. 414). Плоскость x O z является плоскостью максимальной жесткости, поскольку прогиб при изгибе балки на этой плоскости минимален. В Jy^>Jz, как и в рассмотренных примерах, находится CP, поэтому плоскость изгиба
отклоняется от плоскости максимальной жесткости, чем от плоскости внешней силы. Эта разница больше, поскольку отношение^велико. Смысл есть、 ЮЖД Узкое поперечное сечение и высокое поперечное сечение§ 158 с соотношением основных моментов] определение деформации при косом изгибе 491 Инерция очень велика, и уже небольшое отклонение от максимальной
- жесткости рабочей поверхности внешней силы вызывает очень большое отклонение изгибной поверхности балки. До тех пор, пока внешняя сила для балки этого сечения расположена в плоскости максимальной жесткости x OZ, прогиб расположен в той же плоскости, момент инерции Jy должен давать отклонение от оси Oz на небольшой угол<p, важный для плоскости внешней силы, но конструкторы не очень часто полагаются на ось y, она
не изменяется. Чтобы оценить это явление, рассмотрим численный пример. Возьмем деревянные балки с секциями(рис. 409) имеет высоту h=20 см, ширину 6=6 см.* Девятьсот третий год Р3. Девяносто. Jy= = 4000 см\Jz= = 360 см^отношение момента инерции равно _4 0 0 0 −360 1 • Тогда, когда действующая поверхность внешней силы отклоняется от оси Z Фигура. Четыреста пятнадцать / Поверхность кривизны Существует только 5°. tg a=tg<p= = 0,0875- 11 = 0,9 6 3 И^4 4°. Отклонение в направлении оси Y будет приблизительно равно отклонению в направлении оси z: fy=fz tg a=0. 963f2.
В то же время, когда сила отклоняется от плоскости максимальной жесткости, Людмила Фирмаль
нормальное напряжение значительно возрастает. Таким образом, в приведенном примере максимальное нормальное напряжение (по сравнению со случаем плоского изгиба при изгибе с<p=0) равно (см. уравнение 26.6): (cos и/sin Y / / h\ / 20*}=(1t g? ) потому что(1 0.0875)1=1.29. Как использовать 415 показывает относительное положение нагрузки, изгиба и нейтральной плоскости. Основные моменты инерции балок существенно отличаются друг от друга, максимальная жесткость (высокая прямоугольная, двутавровая балка, 492 косых изгиба[гл. Но если вы согнетесь по диагонали, это будет неблагоприятно. Поэтому в тех случаях, когда трудно ожидать достаточно точного совпадения плоскости Тонны \ \ Около Около
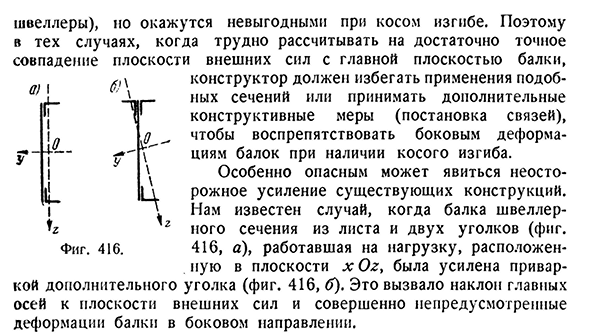
За счет внешних сил, действующих на основную поверхность балки, проектировщик может избежать использования такого сечения или предотвратить боковую деформацию балки при наличии косых изгибов. Особенно опасно неосторожное усиление существующих конструкций. Когда мы знаем этот случай, то пучок швеллерной части листа и двух углов (рис. 416, а), причем нагрузка, расположенная на плоскости х ОЗТ, усиливалась за счет сварки дополнительных углов (рис. 416, б). Это вызвало наклон главного вала в плоскость внешних сил и совершенно непреднамеренную деформацию балки в поперечном направлении
Смотрите также:
| Косой изгиб. Основные понятия | Примеры расчётов при косом изгибе |
| Косой изгиб. Вычисление напряжений | Изгиб балки при действии продольных и поперечных сил. |

