Оглавление:





















Определение давлений в кинематических парах
- Так как каждый механизм 1 класса 2-го порядка состоит из механизма 1 класса 1-го порядка и одной или нескольких последовательно присоединенных к нему двух поводковых групп, то определениеОпределение давлений в кинематических парах 101 давлений в парах следует производить путем последовательного отделения от механизма двух поводковых групп, начиная с последней присоединенной. При определении давления в парах отдельных групп действие звеньев в разрушенных шарнирах заменяется силами. Так, например, если требуется определить давления в парах восьмизвенного механизма, изображенного на фиг. 118, то следует
начинать с последней присоединенной группы — группы B»C»D». Определив давления в парах этой группы и заменив после этого действие звеньев »ѻ и C D » на звенья ВС и В ‘С’ силами, приложенными в сн точках В» и D», следует затем перейти давлений в парах этой группы, кроме \ заданных сил, должна быть принята \ во внимание сила в точке D» со стоV \ \ роны звена C D » предыдущей группы. / \ р \D’ После отделения группы B’C’D ‘ давления в парах отделенной группы BCD должны определяться Фиг. 118. с учетом сил в точках В» и В’ со стороны звеньев предыдущих групп.
После отделения группы BCD и определения давлений в парах этой группы следует Людмила Фирмаль
рассматривать кривошип А В . Приложив в точке В этого звена силу, с которой звено В С действует на кривошип А В , останется только определить величину момента, который должен уравновесить действие звена ВС на кривошип и определить давление в последней паре А . Таким образом, давление в парах хотя бы и очень сложного механизма 1 класса 2-го порядка сводится к определению давлений в парах последовательно отделяемых от механизма двухповодковых групп. Определение давлений в парах двухповодковой группы не может встретить затруднений, так как группа с двумя звеньями и тремя низшими парами является системой статически определимой,
потому что для определения шести неизвестных (по две неизвестных в каждой кинематической паре) можно воспользоваться шестью уравнениями равновесия (по три уравнения для каждого из двух звеньев). Для каждой низшей пары имеем следующие две неизвестные: для вращательной пары известна точка приложения силы (центр шарнира), но неизвестны величина и направление силы; для поступательной пары известно направление силы (перпендикулярно к направляющей), но неизвестны величина и точка приложения силы. Определение давлений в парах
- двухповодковой группы проще всего производить методом планов сил. Рассмотрим, как этот метод применяется при определении давлений в парах группы с тремя вращательными парами и группы с двумя вращательными и одной поступательной парой.102 Кинетостатический расчет плоских механизмов А. Группа с тремя вращательными парами Если на звено действует несколько сил и несколько пар сил, то путем сложения все. силы и пары могут быть приведены к одной силе и одной паре. Если звено находится под действием силы Р и пары с моментом Л4, то действие на звено пары и силы можно заменить, как известно из теоретической механики, действием одной силы. Поэтому, предусматривая общий случай, в
дальнейшем будем считать, что каждое из звеньев группы находится под действием одной силы, при определении величины, линии действия и направления по линии действия которой были приняты во внимание все силы и пары, в том числе и силы инерции. Обозначив через Р 2 (фиг. 119, а) силу, действующую на звено ВС, и через Р3 — силу, действующую на звено CD, будем определять давления в парах В, С и D. Индекс у буквы Р указывает номер звена, на которое действует внешняя заданная сила. Силу со стороны одного звена на другое условимся обозначать буквой Р с двумя индексами, первый из которых будет указывать номер звена, со стороны которого сила действует, а второй — номер звена, на которое производится действие. Например, Р 23 — сила со стороны звена 2 на звено 3, Р32 — сила со стороны звена 3 на звено 2. В точке
В будем считать группу связанной с не изображенным на фигуре звеном /, в точке D — со Людмила Фирмаль
звеном 4 и в соответствии с этим силы в точках B n D будем обозначать Р 12 и Р 43 или В 21 и Р 34 в зависимости от того, со стороны каких звеньев действие сил будет рассматриваться. Входя в состав механизма, группа BCD находится в движении, но так как при определении сил Р 2 и Р3 были учтены и условно перенесенные на звенья группы силы инерции, то в момент, соответствующий изображенному на фиг. 119, а положению группы, группа согласно правилу Даламбера может рассматриваться как находящаяся в равновесии под действием всех внешних сил. Группа находится под действием четырех сил: двух активных сил Р 2 и Р3 и двух сил реакций Р12 и Р 43.Определение давлений в кинематических парах 103 Если плоская система под действием внешних сил находится в равновесии, то векторы этих сил, пристроенные последовательно
один к другому, образуют, как известно, замкнутую фигуру; в этой замкнутой фигуре любой вектор является вектором силы, уравновешивающей действие остальных сил. Замкнутая фигура, образованная векторами находящихся в равновесии сил, называется планом сил. План сил для группы BCD мы не можем сразу построить, так как величин и направлений реактивных сил Р12 и Р43 не знаем, но это затруднение можно преодолеть следующим образом. Не зная величины и направления силы Р12, мы можем определить составляющую этой силы в направлении, перпендикулярном к звену ВС. Обозначив через Р?2 эту составляющую и через Р?2 составляющую в направлении по звену ВС, величину силы PJ2 определяем из уравнения моментов относительно точки С: так как момент направленной по звену ВС силы Р\2 равен нулю, то момент силы Р 2 уравновешивается только моментом силы Р]2. Поэтому рт i р h 1 12* ВС г 2п 29 откуда Р{2 тежу. , где h2 — плечо силы Р2, определяемое по
чер Момент силы Р 2 стремится вращать звено ВС вокруг точки С против часовой стрелки, поэтому момент силы Р]2 должен быть направлен по часовой стрелке и, следовательно, сила Р]2 должна быть направлена перпендикулярно звену ВС вверх. Разлагая силу Р43 на силу Р4з, направленную перпендикулярно к звену СО, и силу Р?3, направленную по звену СО, из уравнения моментов относительно точки С получаем где Л3 — плечо силы Р3 , определяемое по чертежу. После разложения каждой из сил Р1а и Р43 на две составляющие и определения величин и направлений сил Pj2 и Р43 получаются шесть сил, под действием которых группа BCD должна находиться в равновесии. Векторы четырех из этих сил — Р2, Р3, Р]2 и Р43— являются известными по величинам и направлениям, векторы же сил Р?2 и Р43 известны только по линиям действия. Располагая такими данными, можно построить план сил по следующему
векторному уравнению: Р 2 +1 Р 3 +1 Р Х + рп43+ рп + Р Х = 0 . 43 * 1 12 1 12104 Кинетостатический расчет плоских механизмов Построение можно производить следующим образом (фиг. 119, б): 1. Начиная от произвольной точки f чертежа, которую будем называть полюсом плана, проводим последовательно первые три слагаемых векторного уравнения, т. е. пристраиваем последовательно один к другому векторы Р^ Р* и Р . 2. Так как величина силы Р“ неизвестна, а известна лишь ее линия действия, то из конца последнего из векторов — вектора Рх — проводим линию действия вектора Р»д; эта линия должна быть параллельна звену CD и, следовательно, перпендикулярна вектору Р. 3. Не имея возможности продолжать дальше построение плана сил в порядке, который мы избрали, т. е. в порядке, определяемом порядком слагаемых векторного уравнения,
переходим к конечным членам уравнения и проводим вектор Р’ ; так как этот вектор является в уравнении последним и, следовательно, должен замыкать фигуру, то стрелку вектора направляем к полюсу. 4. Предпоследний в уравнении вектор Р» известен только по линии действия, поэтому из начала вектора Р проводим линию действия Р» параллельно звену ВС или, что одно и то же, перпендикулярно вектору Р \ Так как группа BCD находится в равновесии, то векторы должны образовать замкнутую фигуру, поэтому точка пересечения линий действия векторов Р»з и Р» является концом вектора Р»з и началом вектора Р»; Таким образом определяются неизвестные величины сил Р12 и Р43. Давление в паре В со стороны первого звена на второе получается в результате геометрического сложения сил Р» и Р^; вектор равнодействующей этих сил получим, соединив на плане сил начало вектора Р» с концом вектора Рг и поставив на полученном отрезке стрелку против стрелок векторов Р»2 и Р \ Давление в паре D получится в результате геометрического сложения векторов Рз и P»g: линия, соединяющая конец последнего из этих векторов с
началом первого и стрелкой, обращенной против стрелок слагаемых векторов, будет вектором силы Р43. Действующие на группы BCD и внешние силы Р 2 и Р3 и реакции силы Р12 и Р43 должны образовать замкнутую фигуру со стрелками в одном направлении; это и имеет место на построенном нами плане сил. Построив план сил, мы не выявили на нем давления в паре С потому, что сила, действующая со стороны одного звена на другое,Определение давлений в кинематических парах 105 не является внешней силой, действующей на группу BCD, так как внутри группы сила Р 23 уравновешивается равной ей и противоположно направленной силой Р32. Чтобы определить величину и направление силы, с которой одно из звеньев группы давит на другое, необходимо построить план сил для какого-
либо одного из звеньев. Звено ВС находится в равновесии под действием трех сил — Р 2, Р12 и неизвестной пока силы Р32. План сил для звена ВС должен представлять собой треугольник, образованный векторами этих сил. Приняв во внимание, что на построенном нами плане сил первые два вектора уже проведены, мы можем на том же плане провести и вектор Р32, соединив конец вектора Р 2 с началом вектора Р12 и поставив на полученном отрезке стрелку, обращенную в одном направлении со стрелками векторов Р 2 и Р12. Повернув вектор Р32 на 180°, получим вектор Р 23. Те же векторы Р 23 и Р32 мы получим, рассматривая равновесие одного звена CD. При построении плана сил целесообразно проводить векторы последовательно в том порядке, какой был указан выше. Нетрудно убедиться в том, что если к концу вектора Рз пристроить вектор Р2 вместо вектора Р^, а этот последний вектор пристроить к полюсу /, то для определения
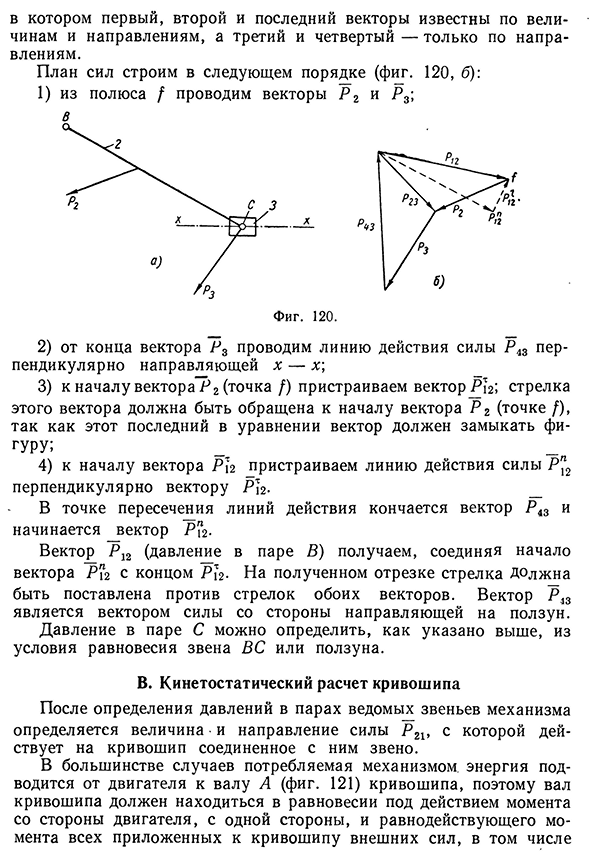
давления в паре С придется строить отдельный план сил для какого-либо из звеньев. Б. Группа с двумя вращательными и одной крайней поступательной парой Такая группа (фиг. 120, а) входит в состав кривошипно-шатунного механизма, имеющего, как уже было отмечено выше, весьма широкое распространение в технике. Обозначив через Р 2 силу, действующую на второе звено (звено ВС), и через Р3 — силу, действующую на третье звено (ползун), определим давления в парах В, С ив поступательной паре ССХ, где Сх — точка на неподвижной направляющей х — х, принадлежащей не входящему в группу неподвижному четвертому звену. Силы Р 2 и Р3 заданы и, следовательно, известны по величинам, линиям действия и направлениям по линиям действия. Реакция Р12 в паре В неизвестна ни по величине, ни по направлению, точка ее приложения известна. Реакция Р43, т. е. сила со стороны направляющей на ползун, может быть направлена только по перпендикуляру к направляющей,
величина ее и точка приложения неизвестны. Разложив силу Р^ на силы Р^ и Р» и определив величину и направление силы Р^2, как это было сделано выше, из условия равновесия группы получаем векторное уравнение 0,106 Кинетостатический расчет плоских механизмов в котором первый, второй и последний векторы известны по величинам и направлениям, а третий и четвертый — только по направлениям. План сил строим в следующем порядке (фиг. 120, б): 1) из полюса f проводим векторы Р 2 и Р3; 2) от конца вектора Р3 проводим линию действия силы Р43 перпендикулярно направляющей х — х\ 3) к началу вектора Р 2 (точка /) пристраиваем вектор РЬ; стрелка этого вектора должна быть обращена к началу вектора Р 2 (точке /), так
как этот последний в уравнении вектор должен замыкать фигуру; 4) к началу вектора Р12 пристраиваем линию действия силы Р»2 перпендикулярно вектору Р12. _ В точке пересечения линий действия кончается вектор Р43 и начинается вектор Р[2-Вектор Р12 (давление в паре В) получаем, соединяя начало вектора Р\2 с концом Р\2. На полученном отрезке стрелка Должна быть поставлена против стрелок обоих векторов. Вектор Р13 является вектором силы со стороны направляющей на ползун. Давление в паре С можно определить, как указано выше, из условия равновесия звена ВС или ползуна. В. Кинетостатический расчет кривошипа После определения давлений в парах ведомых звеньев механизма определяется величина и направление силы Р21, с которой действует на кривошип соединенное с ним звено. В большинстве случаев потребляемая механизмом,
энергия подводится от двигателя к валу А (фиг. 121) кривошипа, поэтому вал кривошипа должен находиться в равновесии под действием момента со стороны двигателя, с одной стороны, и равнодействующего момента всех приложенных к кривошипу внешних сил, в том числеОпределение давлений в кинематических парах 107108 Кинетостатический расчет плоских механизмов и силы Р 21, — с другой. Если кривошип находится под действием только силы Р 21 и условно перенесенной на него центробежной силы инерции, то момент со стороны двигателя будет равен М = = —Р 21 • h21, где h21 — плечо силы Р 21. При определении давления в паре А, т. е. силы Р41 со стороны неподвижного (четвертого) звена на кривошип (первое звено), на плане сил должен быть проведен вектор Р 21, векторы всех действующих на кривошип заданных сил и условно перенесенная на
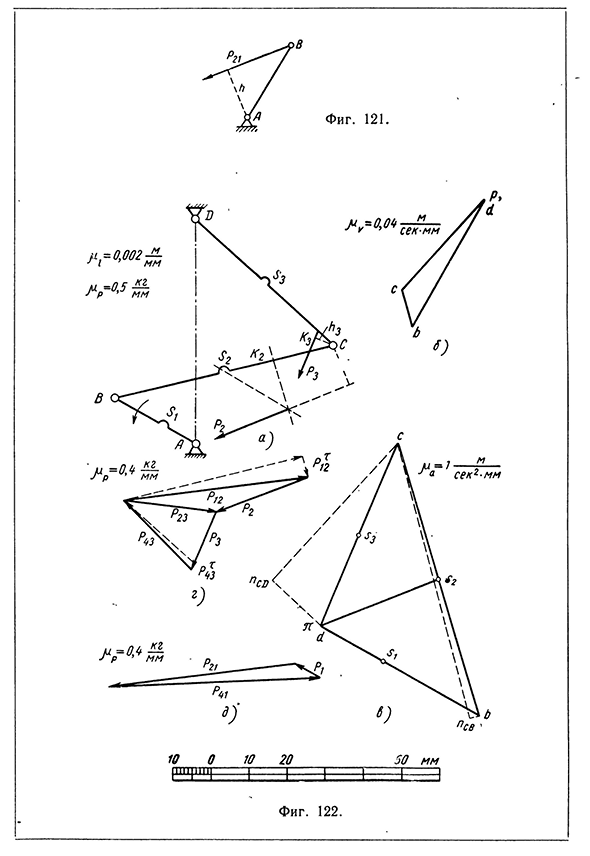
кривошип сила инерции. Вектор, подлежащей определению силы Р41, должен соединять конец последнего из векторов с началом первого. Г. Числовые примеры кинематического анализа и кинетостатического расчета Пример 1. Определить давления от сил инерции в кинематических парах шарнирного четырехзвенного механизма в положении, изображенном на фиг. 122, а, по следующим данным: 1) длины звеньев: 1дв — 50 мм, 1вс =120 мм, Iqd — Ю0 мм, 1дв = 120 мм; 2) положения центров тяжести S звеньев: = 20 мм, Ibsz — 60 мм, IdSz = = 50 мм; 3) моменты инерции J второго и третьего звеньев относительно осей, проходящих через центры тяжести: J 2 = J3 — 5-10-4 кг-м-сек2; 4) веса G звеньев: Gi — 1,5 кг, 6 2 = 3 кг, G3 = 2,5 кг; 5) число оборотов кривошипа АВ, вращающегося против часовой
стрелки с постоянной скоростью, п = 300 об/мин. Номера звеньев указаны на фиг. 122, а. Давление в парах будем определять методом планов сил. Для построения планов сил необходимо предварительно определить величины, линии действия и направления по линиям действия сил инерции в звеньях. Для определения сил инерции нужно построить план ускорений, а для получения необходимых данных для построения этого плана надо построить план скоростей. Поэтому графический расчет должен начаться с построения плана скоростей. 1. План скоростей Абсолютная скорость точки В: VB = Ia b -u>i = 0,05 м сек-1 — 1,57 м/сек. Выбрав масштаб = 0,04 м/сек-л/ж,»определяем длину вектора pb скорости vb-pb — ив • р-v = 1,57 м/сек : 0,04 м/сек-мм = 39,25 мм. Скорость точки С определяем по двум векторным уравнениям: се = св + vcb> vc — vd + vcd • В соответствии с первым уравнением проводим вектор pb перпендикулярно к АВ от полюса р
вниз налево (фиг. 122, б) и из конца этого вектора — линию действия исв перпендикулярно к ВС. В соответствии с вторым уравнением конец вектора pd скорости vd помещаем в полюс, так как vb = 0, и затем из полюса проводим линию действия скорости vcd перпендикулярно к CD. В точке с пересечения линий действия получаем конец вектора рс скорости vcПлан скоростей получается таким образом в виде треугольника pbc.Определение давлений в кинематических парах 109 Пользуясь планом скоростей, определяем необходимые для построения плана ускорений величины скоростей: сев — bepv = 10 м м -0,04 м/сек-мм = 0,4 м/сек, vcd = pc-fv — 33 мм-0,04 м/сек-мм — 1,32 м/сек. 2. План ускорений Определяем величины,
необходимые для построения плана ускорений’ а в = а в = v2B : 1дв = (1,57 м/сек)2 : 0,05 м = 49 м/сек2} °C в ~ v cb : 1в с — (04 м/сек)2 : 0,12 м =1,3 м/сек2} °cd — v cd : ^cd — (1,32 м/сек)2 : 0,1 м = 17,4 м/сек2 . Выбрав масштаб р-а — 1 м/сек2-мм, вычисляем длины векторов: кЬ = ав : ра = 49 м/сек2 : 1 м/сек2 -мм = 49 мм} Ьпсв — ^ с в : ~ м/сек2 : 1 м/сек2 -мм = 1,3 мм} nncD = a cD : На — 17,4 м/сек2 : 1 м/сек2 -мм — 17,4 мм. Ускорение точки С определяем по двум векторным уравнениям: ас — ав-~ ав в + ахс в , ас — ав~{o!qD + axC D . В соответствии с первым уравнением проводим (фиг. 122, в) вектор тс b параллельно АВ, направляя его от полюса вниз направо, так как ускорение точки В в механизме направлено от точки В к точке А. От точки b проводим вектор Ьпсв направляя его параллельно ВС вниз налево, так как ускорение а!^в направлено в механизме от точки С к точке В. От
точки пев проводим линию действия ускорения ахс в . В соответствии с вторым уравнением конец вектора гс d помещаем в полюс, так как ускорение ав неподвижной точки D равно нулю. Из полюса проводим вектор к псп параллельно CD, направляя его вверх налево, так как ускорение а^в направлено в механизме от точки С к точке D. Отточки ncD проводим линию действия ускорения axCD до пересечения ее с линией действия ускорения ахс в в точке с. Соединив точку с с точками тс и Ь, получаем план ускорений в виде треугольника -гс Ьс. Для определения ускорений центров тяжести звеньев определяем сначала положения точек si, S2 и s3 на векторах плана ускорений: -rcSi = nb= 49 • — 19,6 мм} 1ав 50 ™» = с т й = 7 6 ^ = 3 8 м м > ns3 = tzc— 53= 26,5 мм. Idc 100но Кинетостатический расчет плоских
механизмов Проведя вектор получаем длину его равной 34,5 мм. Ускорения центров тяжести: = rcsp fjca = 19,6 ММ’1 м/сек2 -мм = 19,6 м/сек2} а$2 = Ks2 -^a = 34,5 мм 1 м/сек2 -мм = 34,5 м/сек2} aSst = rcs3 Ра — 26,5 мм-1 м/сек2 -мм = 26,5 м/сек2 . 3. Силы инерции Массы звеньев: тг = 1,5 к г : 9,8 м/сек2 = 0,153 кг-сек2/м} /п2 = 3 к г : 9,8 м/сек2 = 0,306 кг-сек2/м} т3 = 2,5 к г : 9,8 м/сек2 = 0,255 кгсек2/мВеличины сил инерции: Р х = m ^asi = 0,153-19,6 = 3 кг} Р2 — f^2,a S2 = 0,306-34.5 = 10,6 кг} Р3 = m3 >ass = 0,255-26,5 »= 6,75 кг. Ускорение центра тяжести Si звена Л В, вращающегося с постоянной скоростью, направлено по линии АВ к центру вращения. Следовательно, сила инерции Pi направлена по
линии АВ вверх налево, т. е. в сторону, обратную ускорению as^ Вектор силы Pi на фиг. 122, а не проведен. Звено ВС совершает сложное движение, которое мы рассматриваем как поступательное с ускорением точки В и вращательное вокруг этой же точки. Сила инерции Ръ звена ВС получается таким образом, как геометрическая сумма двух сил: силы инерции Р2 в поступательном движении и силы инерции Р2 во вращательном движении. Так как в поступательном движении звена ускорения всех точек его равны и параллельны, то Р2 — mz-ciBi где ав — ускорение центра тяжести S% в поступательном движении сточкой В. Сила Р»2 = m2-as2B> где а$2в — ускорение центра тяжести S 2 во вращательном движении. Линия действия силы Pi проходит через центр тяжести S 2, линия действия силы Р2 — через центр качания К 2, находящийся от центра вращения, т. е. точки В, на расстоянии 1вк, IBS. + — IBS. + 05306°0,06~ ~ 0106 М + 01027 м =“ 87 М М Проведя через точку S 2 линию действия силы Р2, параллельную
вектору к b плана ускорений, и через точку К 2 линию действия силы Р»2, параллельную вектору 6s2, в точке пересечения получаем точку приложения равнодействующей Р 2. Величина Р 2 выше уже определена, линия действия ее — параллельна вектору и ускорения as2, направление по линии действия— обратно ускорению а$2. Звено CD совершает вращательное движение с неравномерной скоростью. Сила Р3 направлена по линии действия параллельной вектору тс s3 ускорения as2 в сторону,Определение давлений в кинематических парах 111 обратную этому ускорению. Точка приложения силы Р3 — центр качания /С2, находящийся от центра вращения, т. е. точки D, в расстоянии, равном iDKs = Id s, = = Z d s ’ + 0,255°0,05 = 0 ,0 5 M + °’°3 9 M = 8 9 MM‘ 4. Давления в кинематических парах • Внешние силы,
действующие на группу BCD, должны удовлетворять векторному уравнению Р2 + Рз + ? 4 з + Л 2 = 0. План сил в соответствии с этим уравнением мы не можем построить, так как силы Р43 и Р12 известны лишь по точкам их приложения, величины же и направления этих сил неизвестны. Поэтому каждую из этих сил разлагаем на тангенциальную слагающую, направленную перпендикулярно к звену, и нормальную слагающую, направленную по звену. При этом векторное уравнение приобретает следующий вид: Ъ + Рз + ?43 + Л»з + РЪ + РХ12 = 0. Величину Р 43 определяем из уравнения моментов сил, действующих на звено CD, относительно точки С? Моменты сил Р23 и Р 43 равны каждый нулю, так как линии действия этих сил проходят через точку С; поэтому уравнение моментов получается в виде Рз^з — где h3 — плечо силы Р 3, определяемое по чертежу (фиг. 122, а). Так как длина h3 получается равной 10 мм, то сила Р43 получается равной Р43 — P3 -h3 : Icd = 6,75 кг -10 мм : 100 мм — 0,675 кг. Величину PJ2
определяем аналогичным образом из уравнения моментов сил, действующих на звено ВС, относительно точки С: Р]2 = ^2’^2′ 1вс == Ю,6 кг-24 мм : 120 мм = 2,12 кг. Выбрав масштаб р р = 0,4 кг/мм, определяем длины векторов сил: Р2 = 10 6 к г: 0,4 кг/мм = 26,5 мм; Р3 = 6,75 к г : 0,4 кг/мм = 16,9 мм; Р43 = 0,675 к г : 0,4 кг/мм == 1,69 мМ; Р|2 == 2,12 к г : 0,4 кг/мм 5,3 мм. Строим план сил: проводим векторы сил Р 2 и Р3 (фиг. 122, г), затем из конца последнего вектор Р43, направляя его перпендикулярно к CD вверх направо, так как при таком направлении силой Рх43 создается момент, противодействующий моменту силы Р3 относительно точки С; из конца вектора Р43 проводим линию действия силы Р43 параллельно CD. Не имея возможности пристроить к вектору Р43, длина которого остается пока неизвестной, вектор Pf2 пристраиваем к вектору Р 2 последний в
уравнении вектор Рт12, направляя его перпендикулярно к ВС вниз направо,112 Кинетостатический расчет плоских механизмов так как при таком направлении силой Р[2 создается момент, противодействующий моменту силы Р 2 относительно точки С. Из начала вектора Pj2 проводим линию действия Р^2 До пересечения с линией действия P j3 . Соединив точку пересечения линий действия Р 43 и Р12 с началом вектора Р2 и концом вектора Р3, получаем план сил, соответствующий векторному уравнению ^2 + 3 + ^43 + ^12 = 0. Измерив длины векторов Pi 2 и Р43, получаем давление в паре В Р12 = 50 мм-0,4 кг/мм = 20 кг; давление в паре D Р43 = 26 мм-0,4 кг/мм = 10,4 кг. Для определения давления в паре С необходимо построить план сил для звена ВС или CD. План сил для звена CD надо строить по векторному уравнению ?з + ^43 + Ръз — 0. Первые два вектора на фиг. 122, г уже проведены, остается провести замыкающий треугольник
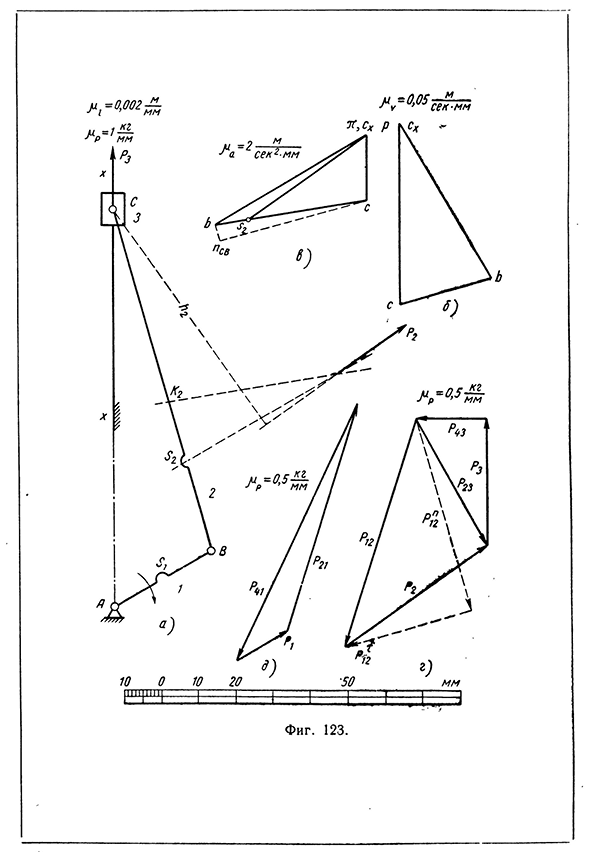
сил вектор Р23. Проведя этот вектор и измерив его длину, получаем давление в паре С Р23 = 25 лл-0,4 кг/мм = 10 кг. План сил для кривошипа надо строить по уравнению Л + ?21+Р41 = 0. Проведя векторы Pi и Р 21 (сила Р 21 равна силеР12 и направлена в обратную сторону) и соединив начало первого из них с концом второго, получаем вектор силы Измерив длину этого вектора, получаем давление в паре А Р4Х = 56 лш«0,4 кг/мм — 22,4 кг. Пример 2. Определить давления в кинематических парах кривошипно-шатунного механизма в положении, изображенном на фиг. 123, а, по следующим данным: 1) длины звеньев: 1дв = 60 мм, 1вс = 190 мм; 2) положения центров тяжести S звеньев: /^Si = 30 мм, IbSz = 50 мм; центр тяжести ползуна в точке С; 3) момент инерции шатуна ВС
относительно центра тяжести J 2 — = 5 -10-4 кг-м-сек2; 4) вес G звеньев: Gi = 1,57 кг, G2 = 2,94 кг, G3 — 4,9 кг; 5) число оборотов кривошипа АВ, вращающегося по часовой стрелке с постоянной скоростью, п = 382 об/мин. Номера звеньев указаны на фиг. 123, а. 1. План скоростей Абсолютная скорость точки В: vB = Ia b ‘^ i = м сек-1 — 2,4 м/сек. Строим план в масштабе p-v = 0,05 м/сек-мм. Длина вектора скорости vb pb = vb ‘ pv = 2,4 м/сек: 0,05 м/сек-мм — 48 мм. Скорость точки С определяем по двум векторным уравнениям: VC = VB + VCB’, СС = VC x + VCCX -Определение давлений в кинематических парах 113 8 Зиновьев 612114 Кинетостатический расчет плоских механизмов В соответствии с первым уравнением проводим вектор pb
перпендикулярно к АВ от полюса р вниз направо (фиг. 123, б) и из конца этого вектора — линию действия vqb перпендикулярно к ВС. В соответствии с вторым уравнением конец вектора рсх скорости vcx неподвижной точки Со лежащей на направляющей х — х, помещаем в полюс, так как vqx = 0, а’затем из полюса проводим линию действия скорости vccx параллельно направляющей. В точке пересечения линий действия получаем конец вектора рс скорости точки С. План скоростей получается в виде треугольника pbc. Пользуясь построенным планом, определяем необходимую для построения плана ускорений величину скорости vcb-vcb = Pv — 25 jwjw-0,05 м/сек-мм = 1,25 м/сек. 2. План ускорений Определяем величины, необходимые для построения плана ускорений: о-в = а в = = (2,4 м/сек)2 : 0,06 м = 96 м/сек2; а с в — v cb : = (1,25 м/сек)2 : 0,19 м — 8,2 м/сек2 .
Выбрав масштаб плана = 2 м/сек2 -мм, вычисляем длины векторов: izb = ав : Ра = 96 м/сек2 : 2 м/сек2-мм = 48 мм; Ъпсв — а с в ’ На — 6,2 м/сек2 : 2 м/сек2 -мм = 4,1 мм. Ускорение точки С определяем по двум векторным уравнениям: (1с = «в + а с в + а с в ; ас = aCjc + апс с * + с?С С х . В соответствии с первым уравнением проводим (фиг. 123, в) вектор тс b параллельно АВ, направляя его от полюса вниз налево, затем отточки b вектор Ьпсв параллельно ВС вниз направо. Величина ускорения ахс в пока неизвестна, поэтому от точки пев проводим линию действия этого ускорения перпендикулярно ВС. В соответствии с вторым уравнением конец вектора tzcx , равного нулю, ускорения асх неподвижной точки Сх помещаем в полюс. Нормальное ускорение ° с с у точки С, движущейся по прямолинейной траектории, также равно нулю, потому что радиус кривизны траектории равен бесконечности. Ускорение известно
только по линии его действия — вдоль направляющей. Проведя из полюса линию действия этого ускорения параллельно направляющей до пересечения с линией действия ахс в , получаем точку с и вектор тс с ускорения яс. План ускорений получается в виде треугольника izbe. Для определения ускорений центров тяжести звеньев необходимо определить предварительно положения на плане точек si и s2 — концов векторов абсолютных ускорений ast и я^2: tcs, = izbJ A S l = 48-|х== 24 мм; lab ЬО bs = be-1_ ^ _ = 41,5 ^ = 9 мм; 2 1вс 190 tcs2 — 39 мм; ~с — 17 мм.Определение давлений в кинематических парах 115 Ускорения центров тяжести: izs2 = 39 мм} пс — 17 мм. = icsr pa = 24 мм-2 м/сек2 -мм = 48 м/сек2} а$2 = ^s2 -p-a = 39 мм-2 м/сек2 -мм = 78 м/сек2} а£ — пс-ра = 17 мм-2 м/сек2 мм = 34 м/сек2 . 3. Силы инерции Массы звеньев: mY — 1,57 кг : 9,8 м/сек2 = 0,16 кг-сек2/м} ш2 = 2,94 кг : 9,8 м/сек2 = 0,3 кг-сек2/м} гп3 — 4,9 к г : 9,8 м/сек2 = 0,5 кг-сек2/м.
Величины сил инерции: Рг = = 0 ,1 6 кг-сек2/м-43 м/сек2 = 7,7 кг} Р2 = m2 -as2 = 0,3 кг-сек2/м-1% м/сек2 = 23,4 кг} Р з ~ т3 -ас = 0,5 кг• сек2/м -34 м/сек2 = 1 7 кг. Сила инерции Р\ направлена по линии действия ускорения в сторону, обратную этому ускорению, т. е. на фиг. 123, а по звену АВ вверх направо. Вектор этой силы на фиг. 123, а не проведен. Разлагая сложное движение звена ВС на поступательное с ускорением точки В и вращательное вокруг этой точки, полную силу инерции получаем как геометрическую сумму двух слагаемых: силы инерции Р’2 в поступательном движении и силы инерции Pg в о вращательном движении. Линия действия силы Р’2 проходит через центр тяжести S2 параллельно вектору тс 6 плана ускорений, так как в поступательном движении с точкой В ускорение центра тяжести равно ускорению
точки В. Сила Pg проходит через центр качания Т<2, находящийся от центра вращения, т. е. от точки В на расстоянии 1вк, — lBSt + — 1 b s+ «о 3-0 05 = 0,05 м + 0,033 м ~ 83 м м » Линия действия р»2 параллельна вектору bs% ускорения центра тяжести S 2 во вращательном движении вокруг точки В. В пересечении линий действия сил Р 2 и Pg получается точка, через которую проходит линия действия полной силы инерции Р 2. Линия действия этой силы параллельна вектору тс s2 ускорения as2 центра тяжестй в сложном движении звена ВС. Величина силы Р 2 определена выше. Сила Р3 проходит через точку С и направлена по линии действия ускорения ас в сторону, обратную этому ускорению. 4. Давления в кинематических парах Разложив
силу Р 12 на нормальную и тангенциальную слагающие, строим план сил для группы ВССХ в соответствии с векторным уравнением ?2+ А + ? 1з+Р?2 + ? ?2 = °8116 Кинетостатический расчет Плоских Механизмов Величину силы определяем из уравнения моментов относительно точки С сил, действующих на звено ВС. Моменты сил Р32 и Р^2 равны нулю, потому что линии действия этих сил проходят через точку С. Плечо силы Р]2 равно Iqq ~ 190 мм; определяемое по чертежу (фиг. 123, а) плечо h2 силы Р2 равно 141. Сила Рх[2 получается равной Р]2 “ ^2^2: 1вс = 23,4 кг-141 мм : 190 мм — 17,5 кг. Выбрав масштаб 0,5 кг/мм, вычисляем длины векторов сил: Р2 = 23,4 к г: 0,5 кг/мм = 46 8 мм; Р3 = 1 7 кг: 0,5 кг/мм = 34 мм; Р~[2 — 17,5 кг : 0,5 кг/мм = 35 мм. Проводим (фиг. 123, г) векторы сил Р 2 и Р 3 и из конца последнего вектора линию действия силы Р43 перпендикулярно к направляющей, так как только по такой линии действия
направляющая может давить на ползун. Проведя к началу вектора Р 2 вектор силы Р]2 перпендикулярно к ВС вниз налево, так как при таком направлении момент силы Р2 уравновешивается моментом силы Р\2, из начала вектора Р\2 проводим линию действия силы Р^2 до пересечения с линией действия силы Р43. Соединив точку пересечения линий действия с началом вектора силы Р 2, получаем векторы сил и Р 43. Измерив длины векторов, получаем: давление в паре В Pi2 = 64 мм-0,5 кг!мм = 32 кг; давление в поступательной паре Р43 = 19 мм0,5 кг/мм = 9,5 кг. Давление в паре С можно определить по плану сил, построенному по векторному уравнению для ползуна, ^ з + Л г з 0 . Первые два вектора на фиг. 123, г уже проведены. Замкнув треугольник сил вектором Р 2з и измерив длину этого вектора,
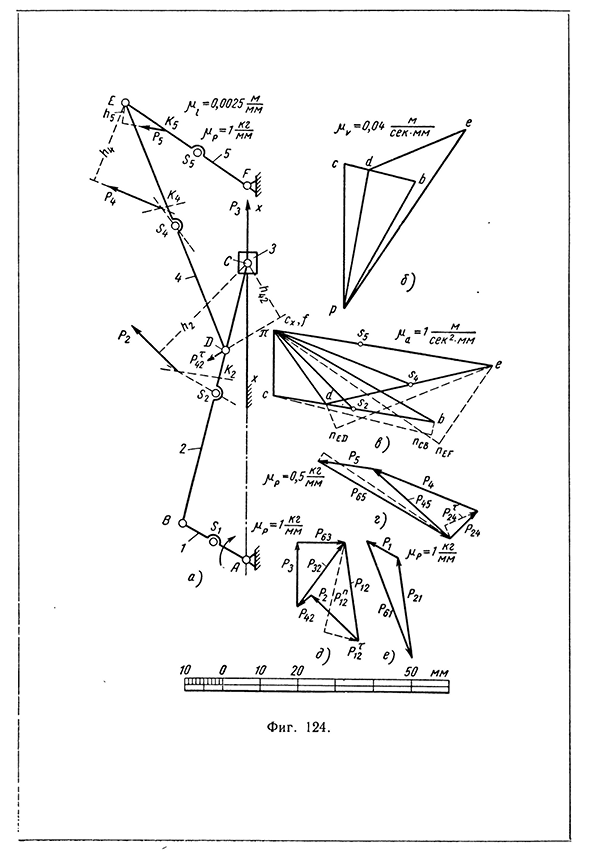
получаем давление в паре С Р 2з = 39 мм -0,5 кг/мм = 19,5 кг. Давление в паре А можно определить по плану сил для кривошипа АВ, построенному по векторному уравнению Л + Р 21 + ? 4 1 « 0 . Величина и направление силы Рг определены выше. Сила Р21 равна силе Р12 и обратно ей направлена. Проведя векторы этих сил (фиг. 123, д) и замкнув треугольник вектором Р41, получаем давление в паре А Р41 = 76 мм -0,5 кг/мм = 38 кг. Пример 3. Определить давления в кинематических парах, угловую скорость и угловое ускорение звена EF шестизвенного механизма в положении, приведенном на фиг. 124, а, по следующим данным: 1) длины звеньев: 1ав = 50 мм, 1вс — 180 мм, Ibd = 120 мм, Ide — 180 мм, Ief = ЮО мм, 1де = 250 мм; 2) положения центров тяжести S звеньев: — 25 мм, ?b s2 = 90 мм, Id s4 = = 90 мм, lps
6 — 40 мм; центр тяжести ползуна в точке С; 3) веса G звеньев: Gi = 1,96 кг, G2 = 5,88 кг, G3 = 9,8 кг, б4 = 3,92 кг, G5 = = 2,94 кг (номера звеньев указаны на фиг. 124, а); 4) моменты инерции J звеньев относительно их центров тяжести: J 2 = = 6-10-4 кг-м-сек2, J^ = 5-Ю -4 кг-м-сек2, 3-10~4 кг/м сек2; 5) число оборотов кривошипа АВ, вращающегося с постоянной скоростью по часовой стрелке, п = 300 об/мин.Определение давлений в кинематических парах 117118 Кинетостатический расчет плоских механизмов 1. План скоростей ив = = 0,05 сек-1 — 1,57 м/сек. Длина вектора vE pb = vE ‘ pv ~ Ь57 м/сек: 0,04 м/сек-мм — 39,2 мм, где масштаб плана скоростей = 0,04 м/сек-мм. Строим план скоростей (фиг. 124, 6): 1) проводим вектор pb
перпендикулярно к АВ, направляя его вверх направо по направлению скорости точки В; 2) для определения скорости vE располагаем двумя векторными уравнениями vc = VB + VCB\ vc = v cx + vccx > где Cx — точка на неподвижной направляющей х — х, расположенная под точкой С; проведя линию действия vE b отточки b перпендикулярно к ВС и линию действия ^ссх параллельно направляющей х — х из полюса (потому что vE = 0, и точка сх попадает, следовательно, в полюс), получаем в точке пересечения линий действия точку с — конец вектора рс скорости сЕ \ 3) разделив отрезок Ьс точкой d в отношении bd : be = 1E d 1вс> проводим pd — вектор vq ; 4) для определения vE располагаем двумя векторными уравнениями: V£ = vd + ve d \ vE = Vp 4VE p, проведя от точки d линию действия vEEf перпендикулярно к DE и из полюса (так цак vp = 0, и точка f попадает, следовательно, в полюс) линию действия vE p перпендикулярно к E
F, получаем в точке пересечения линий действия точку е конец вектора de скорости vE [> и конец вектора ре скорости vE . По построенному плану определяем необходимые для построения плана ускорений скорости: I исв — be[iv — 19,5 мм-0,04 м/сек-мм = 0,78 м/сек\ wE E = de-pv = 28 jlm-0,04 м/сек-мм = 1,12 м/сек\ vE p = pe-pv — 58 jhjw-0,04 м/сек-мм = 2,32 м/сек. Угловая скорость вращения звена EF (звено № 5) <об = vE : 1Е р = 2,32 м/сек : 0,1 м — 23,2 се/с-1. Направление <о5 — по часовой стрелке, что становится очевидным после переноса вектора ре параллельно самому себе до совмещения точек р и Е на фиг. 124, а. 2. План ускорений ав = ад = Сд: 1дв = (1,57 м/сек)2 : 0,05 м = 49,3 м/сек2. Выбрав масштаб р-а = 1 м/сек2, мм, Длину вектора аЕ получаем равной nb = аЕ : Ра = 49,3 м/сек2 : 1 м/сек2 -мм == 49,3 мм.Определение давлений в кинематических парах 119 Проводим
(фиг. 124, в) из полюса тс вектор тс Ь, направляя его параллельно АВ вниз, так как ускорение ав направлено в механизме от точки В к точке А (фиг. 124, а). Определение ускорения ас производим по двум векторным уравнениям яс = яв + я£в + ^СВ’ ~ас=асх + апС сх + а хсС х ■ Величина ускорения аЕ Е — vE E : /де = (0.78 м/сек)2 : 0,18 м — 3,36 м/сек2-, длина вектора этого ускорения Ьпсв == а св : На = 3,36 м/сек2 : 1 м/сек2-мм — = 3,36 мм. От точки b проводим вектор Ьпсв, направляя его параллельно ВС вниз, так как ускорение а^в направлено в механизме по линии ВС от точки С к точке В. От точки пев проводим линию действия ускорения ахс в перпендикулярно к ВС. Перейдя к второму уравнению, точку сх помещаем в полюс, так как ускорение асх = 0 (точка Сх неподвижна). Ускорение ^ссх т а к ж е равно нулю, так как точка С движется по прямолинейной траектории, радиус
кривизны которой равен бесконечности. Поэтому линию действия ^ссх проводим из полюса параллельно направляющей х — х. В точке пересечения линий действия получаем конец вектора тс с ускорения ас. Соединив точки Ъ и с и разделив отрезок Ъс точкой d в отношении bd : be = = Ibd • 1вс и соединив точку d с полюсом, получаем вектор тсd ускоренияав. Ускорение ав определяем по двум векторным уравнениям ав — ав + aB D + «£ = aF + апЕ Р + а’Е Е . Определяем величины нормальных слагающих относительных ускорений: ~ ” 0 ’12 м/сек)2 : 0,18 м== 6,97 « 7 м/сек2\ аВ Р — vB B : Ief — (2,32 м/сек)2 : 0,1 м = 58,8 м/сек2. Определяем длины векторов ускорений a^D и dnEB = a ED : Ра — 7 м/сек2 : 1 м/сек2 -мм — 7 мм; tzhef = aE F : ра = 53,8 м/сек2,: 1 м/сек2,-мм = 53,8 мм. В соответствии с первым уравнением из точки d —
конца уже проведенного вектора тс d — проводим вектор dnEB> направляя его параллельно ED вниз, так как ускорение aB D направлено в механизме от точки Е к точке D, и из конца пев этого вектора линию действия ускорения aB D перпендикулярно к DE. В соответствии с вторым уравнением точку f — конец вектора ускорения ар равного нулю помещаем в полюс, из полюса проводим вектор тс hef и из точки wef — конца этого вектора — линию действия a~E F до пересечения ее с линией действия aB D в точке е.120 Кинетостатический расчет плоских механизмов Соединив точку е с точками d и тс , получаем вектор de ускорения и вектортсе ускорения a^F = а^. По построенному плану ускорений определяем необходимые для определения сил инерции ускорения центров тяжести звеньев: 1) разделив точкой si вектор тс 6 в отношении тс si :тсд — Iasi • Ia b , получаем длину вектора тс si = 24,65 мм и ускорение ast = тс Si-|xa = 24,65 мм-1 м/сек2 мм — 24,65 м/сек2-, 2) разделив
точкой s2 вектор вс в отношении es2 : be — Ie s2 вс и соединив точку s2 с полюсом, получаем длину вектора тс s2 — 30 мм и ускорение а$2 = тс s2 • р-а = 30 мм-1 м/сек2 -м м = 3 0 м/сек2-, 3) длина вектора тсс = 17,5 мм; поэтому ускорение ас = пс-ра = 17,5 мм-1 м/сек2 -мм — 17,5 м/сек2-, 4) разделив точкой s4 вектор de в отношении ds^ : de = Idsi : Ide и соединив точку s4 с полюсом, получаем длину вектора тс s4 — 39 мм и ускорение = TCS4 -p-a = 39 мм-1 м/сек2 -мм — 39 м/сек2-, 5) разделив точкой s5 вектор тс е в отношении тс s5 :тсе — Ife, получаем длину вектора тс s5 = 23,6 мм и ускорение а$8 = тс s5 = 23,6 мм-1 м/сек2 -мм = 23,6 м/сек2. Угловое ускорение звена е5 (звено № 5) получаем, разделив тангенциальное ускорение аЕ точки Е на радиус вращения этой точки, т. е. на длину Л?е = 0,1 м. Длина вектора hef^ — 23 мм,
ускорение ахЕ — ПЕре-ра = 25мм-1 м/сек2 -мм = = 25 м/сек2. Следовательно, еб = 25 м/сек2 : 0,1 м = 250 сек—2. Направление ускорения е5 — по часовой стрелке, что становится очевидным после переноса вектора tzhef параллельно самому себе до совмещения точки тс с точкой Е на фиг. 127, а. 3. Силы инерции Массы звеньев: ш1 = 1,96 кг : 9,8 м/сек2 = 0,2 кг-сек2/м; т2 — 5,88 кг : 9,8 м/сек2 = 0,6 кг-сек/м-, т3 — 9,8 кг : 9,8 м/сек2 — 1,0 кг-сек2/м; т± = 3,92 кг : 9,8 м/сек2 — 0,4 кг-сек2/м; т3 = 2,94 кг : 9,8 м/сек2 = 0,3 кг-сек2/м. Величины сил инерции: Pr = m^asi — 0,2 кг-сек2/м -24,65 м/сек2 — 4,93 кг; Р2 = m2 -as2 = 0,6 кг сек2/м -30 м/сек2 — 18 кг; р 3 — т3 -ас — 1,0 кг-сек2/м -17,5 м/сек2 = 17,5 кг; = m^-asi — 0,4 кг -сек2/м -39 м/сек2 = 15,6 кг; Р5 = m3 -as& = 0,3 кг-сек2/м-23$ м/сек2 — 1 кг. Линии действия сил инерции и направления
по линиям действия следующие. Линия действия силы Pi совпадает с линией действия ускорения аЕ , т. е. с линией АВ. Направление силы Pi — обратно ускорению asx, т. е. вверх налево. Вектор Pi на фиг. 124, а не проведен. Сложное движение звена ВС рассматриваем как поступательное с ускорением точки В и вращательное вокруг точки В. Линия действия силы Р2 в поступательномОпределение давлений в кинематических парах 121 движении проходит через центр тяжести S% параллельно вектору it b — вектору ускорения ав центра тяжести S% в поступательном движении. Линия действия силы Р2 во вращательном движении вокруг точки В проходит параллельно вектору 6s2 ускорения а$2в в этом движении через центр качания К 2, отстоящий от точки В на расстоянии / в к 2 — iBSi + » J2——= iBSt A J = 0,09 м + 0,011 м = 101 мм. U,b-U,uy Через точку пересечения линий
действия сил Р2 и Р2 проходит линия действия силы Р 2, параллельная вектору it s2 абсолютного ускорения as2 центра тяжести S 2 звена ВС. Направление силы Р 2 по линии действия — в сторону, обратную ускорению as2 ._ Сила Р3 направлена вдоль направляющей х — х в сторону, обратную вектору it с ускорения Несложное движение звена DE рассматриваем как поступательное с ускорением точки D и вращательное вокруг точки D. В соответствии с этим через центр тяжести S4 проводим линию действия силы Р4 в поступательном движении и через центр кача ния /С4, находящийся от точки D на расстоянии Id k. = Ids + = 1ds< + -0 4 ^ 0y = 0,09 м + 0,014 м = 104 мм, проводим линию действия силы Р»4 во вращательном движении параллельно вектору ds^ ускорения а$4о центра тяжести S4 в этом движении.. От точки пересечения линий действия сил Р4 и Р4
проводим вектор силы Р4, направляя его параллельно и обратно вектору it s4 ускорения as4. Звено EF совершает вращательное движение с неравномерной скоростью. Точка приложения силы Р5 — центр качания Д5, находящийся от точки F на расстоянии J 3 • 10—4 iFKb = l FSb + «m b ,[F S + ‘0’3,004 = 0 ,0 4 м + 0 ,0 2 5 м = 65 ММ’ Проводим от центра качания вектор силы Р5 , направляя его параллельно вектору it s5 ускорения as5 в обратную этому ускорению сторону. 4. Давления в кинематических парах Давления необходимо определить сначала в парах последней присоединенной группы — группы FED. Звенья этой группы в изображенном на фиг. 124, а положении находятся под действием сил Р4, Р5, Р65 и Р24. Разложив силы Р$5 и Р24 на нормальные и тангенциальные слагающие, будем строить
план сил по векторному уравнению Р< + Рь + Р^5 + ₽65 + ^ 4 + ^24 = Звено EF находится под действием сил и ^65’ Моменты сил Рц И Л>5 относительно точки Е равны нулю (линии действия этих сил проходят через точку Е). Момент силы Р5 равен Р5-h5, где h5 — плечо силы Р5, определяемое по чертежу и равное 15 мм (фиг. 124, а). Из уравнения моментов Рб5′ l EF = Ps’hi получаем Р65 = P5 -h& : Igr = 7 кг-15 мм : 100 мм to 1 кг.122 Кинетостатический расчет плоских механизмов Звено DE находится под действием сил Р4, Р54, Р^4 и Р24Моменты сил Р54 и относительно точки Е равны нулю (линии действия этих сил проходят через точку Е). Момент силы Р4 равен P4 -h4 , где Л4 — плечо этой силы, определяемое по чертежу и равное 57 мм. Из уравнения моментов ?24’IdE “ Лг^4 получаем Р^4 = Р 4А4 : Ide == 15,6 кг -57 мм : 180 мм ъ 5 кг. Выбрав масштаб р-р = 0,5 кг/мм,
определяем длины векторов сил: Р 4 = 15,6 кг : 0,5 кг/мм = 31,2 мм; — 7 кг : 0,5 кг/мм — 14, мм; р£5 = 1 кг : 0,5 кг/мм — 2 мм; Р%4 = 5 кг: 0,5 кг/мм — 10 мм. Проводим последовательно (фиг. 124, г) векторы сил Р4 и Р5 затем вектор Pg5 перпендикулярно к FE вверх направо и из его конца линию действия силы Pg5 параллельно FE. К началу вектора Р4 пристраиваем вектор силы Р^4 и из его начала проводим линию действия силы Р21 Д° пересечения с линией действия силы Р$5. Соединив точку пересечения линий действия с концом вектора Р5 и началом вектора Р4 , получаем план сил, соответствующий векторному уравнению Р4 + ^5 + ^65 + Р‘24 = 0Измерив длины векторов, получаем давление в паре F Р65 = 41 лии • 0,5 кг!мм = 20,5 кг; давление в паре D Р24 — Ю ли/-0,5 кг/мм = 5 кг. Давление в паре Е можно определить по плану сил, построенному для звена DE или
звена FE. Звено FE находится под действием сил Ръ, PQ5 и Р45. Векторы первых двух из этих сил на фиг. 124, г уже проведены; соединив конец вектора Р65 с началом вектора Р5, получаем вектор силы Р45. Измерив длину этого вектора, получаем давление в паре Е будет Р45 = 28 лш-0,5 кг/мм = 14 кг. Группа ВССХ находится под действием сил Р2, Р42, Рз> Р&з и Р12. Разложив последнюю из них на нормальную и тангенциальную слагающие, будем строить план сил по векторному уравнению ? 2 + Л 2 + Р з 4 Р6з + Р ? 2 + Р12 ^ ° -Звено ВС находится под действием сил Р 2, Р42, Р32, Р\2 и ^12Так как моменты силРз 2 и Р^2 относительно точки С равны нулю (линии действия этих сил проходят через точку С), то уравнение моментов
относительно точки С получается в виде Р С — Р2^2 ^42^42» где h2 = 85 мм — плечо силы Р 2, определяемое по чертежу, и h42 — 42,5 мм — плечо силы Р42 (фиг. 124, а). Из этого уравнения получаем п Г т _ PJh + ^42^42 _ 18 кг-85 мм + 5 кг-42,5 мм __Q 7 12————1^с 180“^ У’ г ’Определение давлений в кинематических парах 123 Выбрав масштаб р-р = 1 кг/’мм, определяем длины векторов сил: Р2 — 18 кг : 1 кг/мм — 18 мм\ Р42 = 5 кг : 1 кг/мм — 5 мм\ р 3 = 17,5 к г : 1 кг/мм ~ 17,5 мм\ Р |2 = 9,7 кг : 1 кг/мм — 9,7 мм. Проводим последовательно (фиг. 127, д) векторы Р 2, Р ^, Р3 и из конца последнего линию действия силы Р63. Пристроив к началу вектора Р 2 вектор Р]2, направленный перпендикулярно кВС и вправо, проводим из начала его линию
действия силы Р»2 до пересечения с линией действия силы Р63. Соединив точку пересечения линий действия с началом вектора Р 2, получаем план сил, соответствующий векторному уравнению. + + -!-А з+ А 2 = о. Измерив длины векторов P i2 и PG3, получаем: давление в паре В P i2 = 27 мм• 1 кг/мм = 27 кг\ давление в поступательной паре Р63 = 13 м м -1 кг/мм = 13 кг. Давление в паре С определяется из плана сил для звена ВС, построенного по векторному уравнению Р\2~\Р2 ^42 + Р32 “ ОПервые три вектора на фиг. 124, д уже проведены. Соединив конец вектора Р42 с началом вектора Pi2 , получаем вектор силы Р 32. Измерив длину этого вектора, получаем: давление в паре С Р32 — 22
мм-1 кг/мм — 22 кг. Давление в паре А определяем из плана сил для кривошипа, построенного по векторному уравнению А1 + Л + Ли-о. Величина и направление силы Pi определены выше. Сила P 2i равна по величине силе Р12 и направлена в обратную сторону. Проведя векторы этих сил в масштабе |Лр = 1 кг/мм (фиг. 124, ё) и измерив длину замыкающего треугольник сил вектора Р б1» получаем Давление в паре А Р61 = 34 мм-1 кг/мм = 34 кг.
Смотрите также:
| Кинетостатический расчет плоских механизмов предварительные сведения | Передача вращательного движения гибкими телами. ременная передача |
| Определение сил инерции | Фрикционная передача |

