Оглавление:
Определение абсолютного ускорения точки. Ускорение Кориолиса
Ускорение точки — первая производная по времени от вектора скорости. Поэтому абсолютное ускорение, используя формулу (10.3):
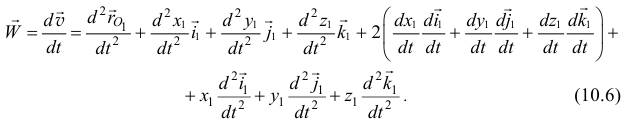
Воспользовавшись правилом остановки, можем найти относительное и переносное ускорения точки.
Положив в (10.6)
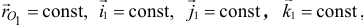
получим относительное ускорение:
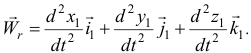
При
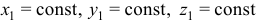
получим переносное ускорение
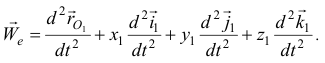
Поэтому из формулы (10.6) следует, что абсолютное ускорение состоит не из двух, а из трех ускорений
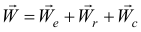
Дополнительное ускорение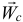 
называется ускорением Кориолиса (по имени ученого, впервые обнаружившего это ускорение), оно равно
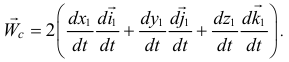
Это дополнительное ускорение появилось из-за того, что переносная скорость зависит от относительного движения, от положения точки на среде, а относительная скорость изменяется за счет переносного движения.
Проще всего определить ускорение Кориолиса в двух частных случаях.
Переносное движение — поступательное движение (система подвижных осей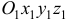 
перемещается поступательно).
Так как подвижные оси при таком движении не поворачиваются, то орты
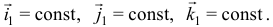
И тогда по (10.9) ускорение Кориолиса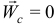 
, а абсолютное ускорение станет суммой лишь двух ускорений
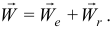
Это понятно, так как переносная скорость точки не будет зависеть от относительного движения, а переносное движение не изменяет направление вектора относительной скорости.
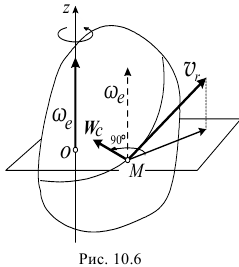
- Переносное движение — вращение вокруг неподвижной оси.
Пусть подвижная система осей 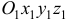вращается вокруг неподвижной оси 
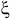с угловой скоростью 
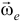(рис. 10.5).
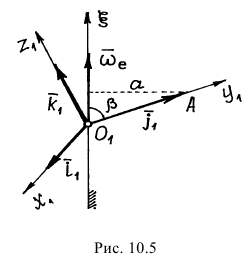
Представим орты осей как радиусы-векторы точек, расположенных на их концах. Тогда производные от орт по времени можно рассматривать как скорости этих точек.
Например, скорость точки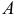 
на конце вектора 
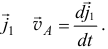а вектор скорости 
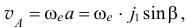а вектор скорости 
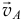направлен перпендикулярно 
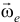и 
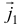в сторону вращения, то 
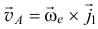(см. 9.1).
Поэтому
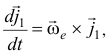
аналогично
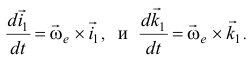
По 10.9 ускорение Кориолиса
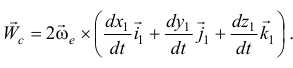
И, учитывая (10.4), получим
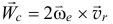
Ускорение Кориолиса есть удвоенное векторное произведение вектора угловой скорости переносного движения на вектор относительной с корост и т о чки.
Величина его
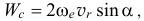
где 
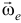— острый угол между векторами 
и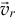 
.
Замечание. Можно доказать, что этот результат верен при любом переносном движении, не только при вращении вокруг неподвижной оси.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Абсолютное, относительное и переносное движения точки |
| Определение абсолютной скорости точки |
| Сложение вращений тела вокруг двух осей |
| Аксиомы динамики в теоретической механике |
