Оглавление:
Операции над матрицами
Матрицей размеров 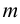 на
на 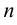 или
или 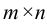 — матрицей называется прямоугольная таблица вида
— матрицей называется прямоугольная таблица вида
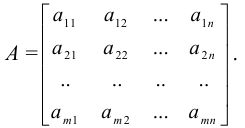
Отдельные числа матрицы называются ее элементами. Элементы 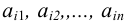 составляют
составляют 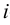 -ю строку, а элементы
-ю строку, а элементы 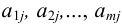 —
— 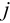 -й столбец матрицы;
-й столбец матрицы; 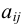 — элемент матрицы
— элемент матрицы  , стоящий на пересечении
, стоящий на пересечении 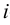 -й строки и
-й строки и 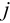 -го столбца. Строки и столбцы матрицы называют ее рядами.
-го столбца. Строки и столбцы матрицы называют ее рядами.
Матрица, у которой число строк 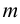 равно числу столбцов
равно числу столбцов 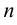 , называется квадратной. Порядком квадратной матрицы называется
, называется квадратной. Порядком квадратной матрицы называется
число ее строк (или столбцов).
В квадратной матрице
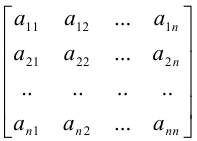
элементы 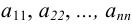 составляют главную диагональ.
составляют главную диагональ.
Матрица, элементами которой являются числа, называется числовой.
Две матрицы называются равными, если они одинаковых размеров и элементы одной матрицы равны соответствующим элементам другой.
Нулевой называется матрица, все элементы которой равны нулю. Нулевую матрицу будем обозначать буквой 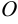 .
.
Диагональной называется квадратная матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю.
Квадратная матрица, у которой каждые элементы, стоящие вдоль главной диагонали, равны единице, а все остальные элементы нули, называется единичной. Единичную матрицу будем обозначать буквой 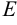 .
.
Если в матрице поменять столбцы на строки, то получим новую матрицу, называемую транспонированной к данной. Матрицу транспонированную матрице  будем обозначать
будем обозначать 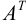 .
.
Операция сложения вводится только для матриц одинаковых размеров.
Суммой (разностью) двух матриц 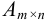 и
и 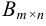 называется матрица
называется матрица 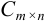 такая, что
такая, что 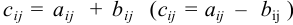 , (
, (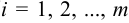 ;
; 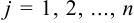 ). Сумма ( разность) матриц
). Сумма ( разность) матриц  и
и 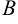 обозначается
обозначается 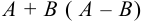 .
.
Произведением матрицы 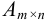 на число
на число 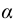 (или числа
(или числа 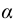 на матрицу
на матрицу 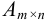 ) называется матрица
) называется матрица 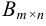 такая, что
такая, что 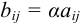 . Произведение матрицы
. Произведение матрицы  на число
на число 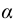 обозначается
обозначается 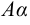 или
или 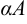 .
.
Матрицу (-1)  будем называть матрицей, противоположной
будем называть матрицей, противоположной  , и обозначать
, и обозначать  .
.
Матрицу  можно умножить на матрицу
можно умножить на матрицу 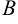 , если число столбцов матрицы
, если число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 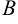 , т. е. если
, т. е. если  — матрица размеров
— матрица размеров 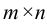 , а
, а 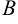 — размеров
— размеров 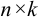 .
.
Произведением матрицы 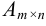 на матрицу
на матрицу 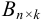 называется матрица
называется матрица 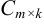 такая, что
такая, что
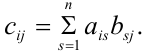
Произведение матрицы  на матрицу
на матрицу 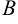 обозначается
обозначается 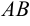 .
.
Из определения следует, что элемент матрицы 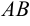 , стоящий в
, стоящий в 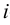 -й строке и
-й строке и 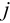 -м столбце, равен сумме произведений элементов
-м столбце, равен сумме произведений элементов 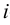 -й строки матрицы
-й строки матрицы  на соответствующие элементы
на соответствующие элементы 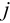 -го столбца матрицы
-го столбца матрицы 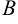 .
.
Заметим, что если матрицу  можно умножить на матрицу
можно умножить на матрицу 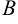 , то отсюда не следует, что
, то отсюда не следует, что 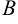 можно умножить на
можно умножить на  , т. е.
, т. е. 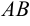 не всегда равно
не всегда равно 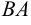 .
.
Задача №1.
Даны матрицы
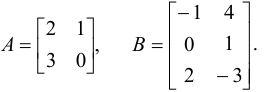
Выяснить, существуют ли произведения 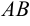 и
и 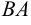 , и, если существуют, то найти их.
, и, если существуют, то найти их.
Решение:
Произведение 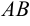 не существует, так как число столбцов матрицы
не существует, так как число столбцов матрицы  не равно числу строк матрицы
не равно числу строк матрицы 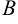 .
.
Произведение 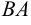 существует и
существует и
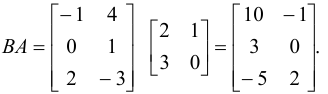
Задача №2.
Найти 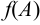 , если
, если 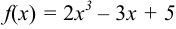 ,
,
Решение:
Подставляя в 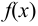 вместо
вместо 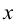 матрицу
матрицу  и учитывая, что
и учитывая, что 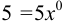 , получим
, получим
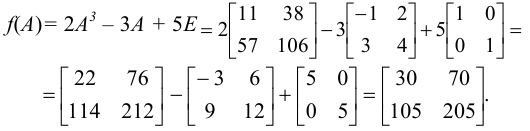
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Определители задачи с решением |
| Обратная матрица с решением задачи |
| Ряды Тейлора и Маклорена задача с решением |
| Применение рядов в приближенных вычислениях задачи с решением |

