Оглавление:
Транспонирование матриц
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной и обозначается 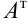 .
.
Пример №1.1.
Транспонируйте матрицу 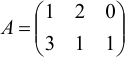
Решение:
Операция транспонирования матрицы  осуществляется следующим образом: первая строка матрицы
осуществляется следующим образом: первая строка матрицы  становится первым столбцом матрицы
становится первым столбцом матрицы  , вторая строка
, вторая строка  — вторым столбцом
— вторым столбцом  , т.е.
, т.е.
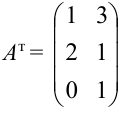
Сложение (вычитание) матриц
Складывать (вычитать) можно только такие матрицы, которые имеют одинаковую размерность.
Суммой (разностью) матриц 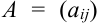 и
и 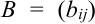 называется матрица
называется матрица 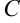 , элементы которой равны суммам (разностям) соответствующих элементов матриц
, элементы которой равны суммам (разностям) соответствующих элементов матриц  и
и 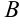 , т.е.
, т.е. 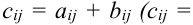
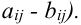
Пример №1.2.
Найдите сумму и разность матриц 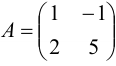 и
и 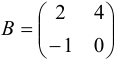
Решение:
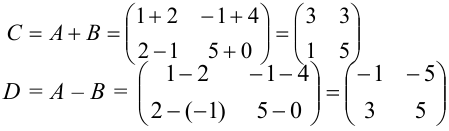
Операция сложения матриц обладает следующими свойствами:
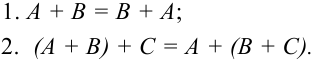
Умножение матрицы на число
Произведением матрицы  на число
на число 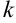
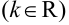 называется матрица
называется матрица 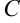 той же размерности, элементы которой равны произведению числа
той же размерности, элементы которой равны произведению числа 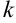 на соответствующие элементы матрицы
на соответствующие элементы матрицы  , т.е.
, т.е. 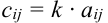
Операция умножения матрицы на число обладает свойствами:
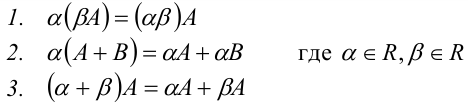
Пример №1.3.
Найдите произведение матрицы 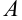 на число
на число 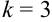
Решение:
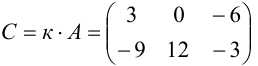
Умножение матриц
Матрицу  можно умножать на матрицу
можно умножать на матрицу 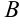 тогда и только тогда, когда число столбцов матрицы
тогда и только тогда, когда число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 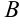 .
.
Произведением матрицы  размера (
размера (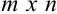 ) на матрицу
) на матрицу 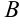 размера (
размера (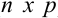 ) называется матрица
) называется матрица 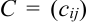 размера (
размера (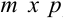 ), элементы которой равны сумме произведений элементов
), элементы которой равны сумме произведений элементов 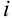 -ой строки матрицы
-ой строки матрицы  на соответствующие элементы
на соответствующие элементы 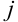 -го столбца матрицы
-го столбца матрицы 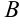 .
.
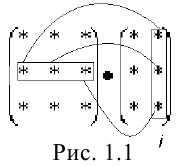
Получение элемента 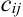 можно представить в виде схемы (рис. 1.1):
можно представить в виде схемы (рис. 1.1):
Пример №1.4.
Найдите произведение матриц 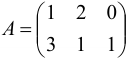 и
и 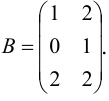
Решение:
Размер матрицы 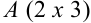 , размер
, размер 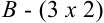 .
.
Число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 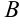 , следовательно, умножение возможно. При этом матрица
, следовательно, умножение возможно. При этом матрица 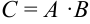 будет иметь размерность
будет иметь размерность 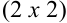 .
.
Найдем элементы 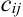 матрицы
матрицы 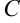 :
:
Для нахождения элемента 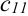 находим сумму произведений элементов первой строки матрицы
находим сумму произведений элементов первой строки матрицы  и первого столбца матрицы
и первого столбца матрицы 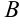 :
:
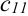 = ( 1 строка
= ( 1 строка  и 1 столбец
и 1 столбец 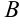 ) = 1 • 1 + 2 • 0 + 0 • 2 = 1;
) = 1 • 1 + 2 • 0 + 0 • 2 = 1;
Аналогично 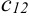 = (1 строка
= (1 строка  и 2 столбец
и 2 столбец 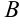 ) = 1 • 2 + 2 • 1 + 0 • 2 = 4;
) = 1 • 2 + 2 • 1 + 0 • 2 = 4;
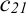 = (2 строка
= (2 строка  и 1 столбец
и 1 столбец 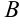 ) = 3 • 1 + 1 • 0+1 • 2 = 5;
) = 3 • 1 + 1 • 0+1 • 2 = 5;
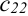 = (2 строка
= (2 строка  и 2 столбец
и 2 столбец 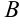 ) = 3 • 2 + 1 • 1 + 1 • 2 = 9.
) = 3 • 2 + 1 • 1 + 1 • 2 = 9.
Получили, что 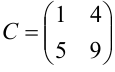 . Ответ:
. Ответ: 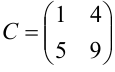
Операция умножения матриц обладает следующими свойствами:
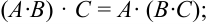
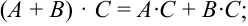
- В общем случае
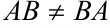 (порядок матриц при умножении важен).
(порядок матриц при умножении важен).
Замечание: Свойством коммутативности обладают произведения:
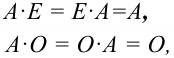
где 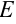 и
и 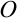 — единичная и нулевая матрицы соответственно.
— единичная и нулевая матрицы соответственно.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Виды квадратных матриц. |
| Равенство матриц. |
| Понятие определителя матрицы. |
| Свойства определителей. |

