Операторный метод расчета переходных процессов. Теорема Хэвисайда
Операторный метод расчета переходных процессов основан на операционном исчислении. Операционный метод решения дифференциальных уравнений отличается от классического метода рядом ценных качеств, главные из них:
1) сложное действие дифференцирования заменяется простым умножением на некоторую переменную » 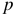 «, которая называется оператором, а действие интегрирования — делением на эту же переменную),
«, которая называется оператором, а действие интегрирования — делением на эту же переменную), 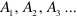 — начальные условия входит в основные уравнения сразу, поэтому не требуется в ходе расчета составлять громоздкие системы уравнений для отыскания постоянных интегрирования по начальным условиям.
— начальные условия входит в основные уравнения сразу, поэтому не требуется в ходе расчета составлять громоздкие системы уравнений для отыскания постоянных интегрирования по начальным условиям.
Основой операционного метода является функциональное преобразование. Это значит, что функция вещественного переменного 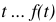 соответственно выражается через функцию комплексного переменного
соответственно выражается через функцию комплексного переменного 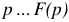 .
.
Используя символы, применяемые в операционном исчислении, основное функциональное преобразование можно записать:

где 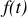 — называется оригиналом функции или начальной функцией, или временной функцией;
— называется оригиналом функции или начальной функцией, или временной функцией;
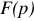 — называется изображением функции
— называется изображением функции 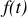 или операторной функцией;
или операторной функцией;  — называется знаком соответствия, острие стрелки которого направляется всегда в сторону начальной функции, т.е. в сторону оригинала.
— называется знаком соответствия, острие стрелки которого направляется всегда в сторону начальной функции, т.е. в сторону оригинала.
Знак соответствия 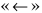 не является обычным знаком равенства, т.к. независимые переменные
не является обычным знаком равенства, т.к. независимые переменные 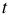 и
и 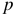 различны по размерности.
различны по размерности.
Начальные или временные функции обозначаются малыми буквами, а их изображения — соответствующими им прописными.
В операционном исчислении оригинал и изображение функции связываются между собой линейным интегральными преобразованиями, называемыми интегралом Лапласа и интегралом Лапласа-Карсона. Последний интеграл более удобен для расчета электрических цепей, поэтому в дальнейшем мы будем пользоваться им.
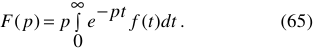

Интеграл Лапласа-Карсона позволяет сложное дифференциальное уравнение изобразить алгебраическим уравнением.
В результате решения алгебраического уравнения мы получаем не функцию вещественного переменного 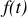 , а лишь ее изображение в виде операционной функции
, а лишь ее изображение в виде операционной функции 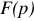 . Поэтому необходимо, теперь, решить обратную задачу: найти по изображению функции ее оригинал.
. Поэтому необходимо, теперь, решить обратную задачу: найти по изображению функции ее оригинал.
Для этого интеграл Лапласа-Карсона должен быть разрешен относительно 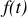 . В общем случае такое решение дано английским математиком Бромвичем и называется интегралом Бромвича.
. В общем случае такое решение дано английским математиком Бромвичем и называется интегралом Бромвича.
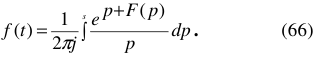
Bee операционное исчисление, таким образом, основано на двух взаимно обратных интегралах: интеграле Лапласа или Лапласа-Карсона и интеграле Бромвича. При этом для операторных величин (токов, напряжений и т.д.) сохраняются законы Ома, Кирхгоффа и все известные методы расчета цепей. Примечания.
Рассмотрим с помощью интеграла Лапласа-Карсона некоторые теоремы операционного метода.
а) Изображение постоянной величины
Пусть
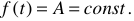
Тогда

Изображение постоянной величины равно самой величине.
б) Изображение алгебраической суммы двух функций
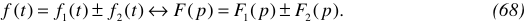
в) Изображение показательной функции

г) Изображение синусоидальных функций

г) Изображение производной функции Для 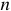 -ой производной имеем:
-ой производной имеем:
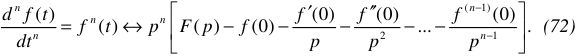
Если
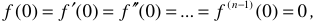
то

д) Изображение интеграла функции
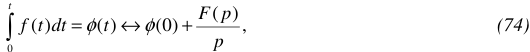
где 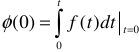 — начальное значение интеграла функции
— начальное значение интеграла функции 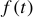 при
при 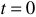 .
.
Если начальное значение интеграла функции при 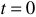 равно нулю, то:
равно нулю, то:

Ход расчетов следующий.
Во-первых, исходная схема преобразуется в операционный вид, рисунок 14. При этом:
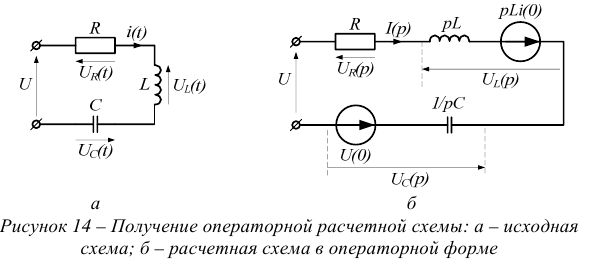
- все постоянные величины: ЭДС источника, активные сопротивления в ветвях имеют своими изображениями такие же постоянные величины;
- все индуктивные реактивные сопротивления имеют своими изображениями
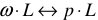 . Если начальное значение тока в катушке не равно нулю, то последовательно с катушкой включается источник постоянного напряжения величиной
. Если начальное значение тока в катушке не равно нулю, то последовательно с катушкой включается источник постоянного напряжения величиной 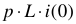 , который направлен по току;
, который направлен по току;
- все емкостные реактивные сопротивления имеют своими изображениями
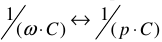 . Если начальное значение напряжение на конденсаторе отлично от нуля и равно
. Если начальное значение напряжение на конденсаторе отлично от нуля и равно 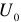 , то последовательно с емкостью включается источник постоянного напряжения величиной
, то последовательно с емкостью включается источник постоянного напряжения величиной 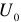 . Направление ЭДС источника — против тока.
. Направление ЭДС источника — против тока.
Затем полученная расчетная схема рассчитывается любым из известных методов расчета цепей. Полученный результат является функцией комплексного переменного 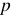 .
.
Первый закон Кирхгофа в операторной форме:

Второй закон Кирхгофа в операторной форме:
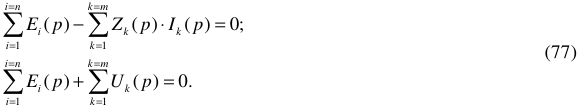
Закон Ома в операторной форме:

Все рассмотренные ранее методы расчета цепей действительны и для расчета переходных режимов операторным методом.
Теорема разложении Хэ в и сайда
Ранее мы показали, что результат расчета цепи будет иметь форму операторной функции.
Решение в таком виде для практики не пригодно, его необходимо привести обратно в функцию от времени.
Выше мы указывали, что для обратного перехода необходимо в общем случае применять интеграл Бромвича. Однако путь этот очень сложен. На практике часто пользуются не интегралом Бромвича, а теоремой разложения Хэвисайда.
Теорема разложения представляет собой готовую формулу для определения оригинала функции 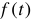 по известному изображению этой функции
по известному изображению этой функции 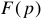 . Она является результатом решения интеграла Бромвича для функции
. Она является результатом решения интеграла Бромвича для функции 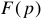 частного вида.
частного вида.
Функция 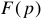 в этом случае должна быть выражена рациональной дробью:
в этом случае должна быть выражена рациональной дробью:
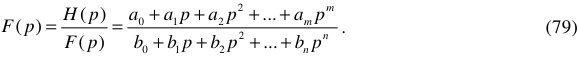

Рациональная дробь (79) кроме того, должна удовлетворять следующим свойствам:
- наивысшая степень оператора
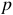 знаменателя
знаменателя 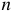 должна быть больше наивысшей степени оператора
должна быть больше наивысшей степени оператора 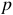 числителя
числителя 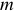 или, в крайнем случае, равна ей
или, в крайнем случае, равна ей 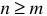 . Это условие для задач прикладного характера почти всегда удовлетворяется.
. Это условие для задач прикладного характера почти всегда удовлетворяется.
- корни
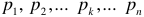 знаменателя
знаменателя 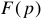 , полученные решением уравнения
, полученные решением уравнения 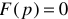 должны быть все простые (отсутствуют корни равные друг другу и кратные корни) и не один из корней не должен ни при каких условиях быть корнем числителя
должны быть все простые (отсутствуют корни равные друг другу и кратные корни) и не один из корней не должен ни при каких условиях быть корнем числителя 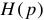 (не обращать числитель
(не обращать числитель 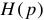 в нуль при подстановке в него
в нуль при подстановке в него 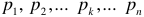 ). Если есть дополнительный
). Если есть дополнительный 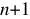 корень, то он может быть равен нулю.
корень, то он может быть равен нулю. - все вещественные корни должны быть отрицательными, а все комплексные — иметь отрицательную вещественную часть. С учетом вышесказанного получится, что первообразная функция
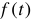 операторной функции
операторной функции 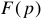 будет иметь следующий вид:
будет иметь следующий вид:
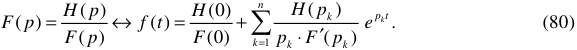
где член 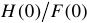 , который получается от подстановки дополнительного нулевого корня
, который получается от подстановки дополнительного нулевого корня 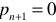 , определяет принужденную составляющую или установившийся режим для постоянного тока или напряжения;
, определяет принужденную составляющую или установившийся режим для постоянного тока или напряжения;
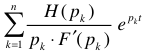 — определяет сумму свободных режимов для тока или напряжения.
— определяет сумму свободных режимов для тока или напряжения.
Выражение (80) называется теоремой разложения. Используя теорему разложения, можно находить начальную функцию по ее изображению, не прибегая к интегралу Бромвича, в этом и состоит основная ценность теоремы.
Эта страница взята со страницы контрольной работы по электротехнике:
Контрольная работа по электротехнике
Возможно эти страницы вам будут полезны:
| Резонанс напряжений в цепи |
| Резонанс токов в цепи |
| Баланс мощности в электрической цепи постоянного тока |
| Графоаналитический метод расчета нелинейных цепей |

