Оглавление:






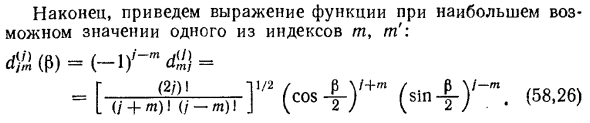

Оператор конечных вращений
- Оператор конечного вращения Вернемся к спинорному преобразованию и покажем проблему Каковы коэффициенты для этого преобразования? На самом деле это выражается углом поворота оси координат. Определив оператор момента (в данном случае спин), Формула 1 + iS (p • ns — оператор вращения Направление определяется единичным вектором n.
- Применяется в Волновая функция частицы со спином 1/2, то есть Ранг, мы должны положить s = d / 2 в этом операторе. Подобно матричной функции Паули (см. Задачу 1) § 55), эта формула линейна с этими матрицами выражение Un = cos (1 2. Особенно при вращении под углом 2 л компоненты спинола Парализовать знак, поэтому они обладают одинаковыми характеристиками Также спиннер нечетного ранга (см. §55 конец).
Оператор Поверните последний угол cp в том же направлении Дано Un = exp (r <^ by / 2) (58,1) (Ср. (15.13)). Людмила Фирмаль
Аналогично найдите следующую матрицу преобразования: Угол (p относительно оси x или y) Tm / m \ = (™ s (<P / 2) i sin (<^ / 2) \ ft, s = (cos (<^ / 2) sin (p / 2) ) \ ^ sin (<^ / 2) потому что (</? / 2) y’sin (<^ / 2) потому (<^ / 2) y (58,4) 270 SPIN GL. VIII Обратите внимание на конкретный случай поворота вокруг оси Y на угол 7G. который φ1 ‘= φ2, φ2’ = -φ \ Это ф1 ‘= фч, ф2’ = ф2. (58,5)
Написать матрицу преобразования легко Свободное вращение координатных осей в зависимости от угла Эй Рера, которая определяет этот ход. Вращение оси, определяемое углом Эйлера ce / 3, 7, поколение Выполнено в 3 этапа. 1) Вращение угла а (0 ^ a ^ 2 тг) Ось 2, 2) Угол / 3 (0 ^ / 3 ^ тг) вращения вокруг новой позиции по оси Y (O N 20, так называемый узелный ряд), 3)
Угол 7 (0 ^ 7 ^ 2 n) вращения Последний круг Положение оси Z (z ‘) 1). Очевидно, что угол CE, / 3 Сферический угол вдоль новой оси z * <^ Для оси xyz: ce = (p, / 3 = 9. По такому методу Осевой затвор, полная матрица преобразования Равен произведению трех матов Ритц (58,3), (58,4): Рисунок 20 U (a, (3, 1) = Uz (1) Uy ((3) Uz (a)). Путем умножения матрицы, наконец, Dim rm (r \ — (cos (/ 3/2) e ^ a + 7) / 2 sin (/ 3/2) e _ * (a_7) / 2 \ (A) / 5,7) -s i n (/ 3/2) e * 0-7) / 2 cos (/ 3/2) e-i (a + T ‘) / 2 J’ ^^ По определению верхний спинор трансформируется.
Как первоклассный спинор. физически Тем не менее, интерес к приложению низок x) Системы x y z и x ‘y’ z ‘правосторонние, как обычно, Квадратная счетная доска поддерживает направление отвертки Положительное направление оси вращения. Определение угла Эйлера, данное здесь (принято в квантовой механике) Приложение) отличается от 35-го определения (т. См. I). Вращение происходит вокруг оси y, а не оси x.
Угол а / 5,7 связаны Угол ip, v, f в т. Я (не путать со сферическим углом ip, v ) через = / 5, / ^ § 58 ОПЕРАЦИОННЫЕ УСЛОВИЯ 271 VRA SCHNE Y 271 Собственные правила трансформации Спинора и их соответствующие номера Ijjjm функции WAVE Объясняется функцией (rn = j, j -1, …, -j) Состояние Xyz системы ординат с определенным значением Момент j и функция одинаковы по отношению к Ось x fyfz f; в первом случае m — это значение j z, во втором случае: т! = цзы Обе функции являются линейными. ми отношения.
Используйте следующий формат Фз ™ = ÅPi ‘У) Фjm’ • (58,7) т! Коэффициент D ^ j (относительно индекса t ‘t) ранг 2 j + 1 матрица-матрица конечного вращения Его элементы являются функцией угла поворота системы a, / 3,7 x fyfz f для xyz. Конструктивное построение матриц конечного вращения Может быть сгенерирован с использованием спинорного представления Функция φ ^ ω. Когда j = 1/2, две функции φ1 / 2m (m = L / 2) Ковариантный спиннер первого ранга. (56.13)
По его словам Обучение (от системы x fyfz f до системы xyz) выполняется Матрица U (58,6), следовательно, Z ^ 1/2) = U 1). Давайте напишем этот элемент В форме где 7 округ т! / 1 / 2-1 / 2 1/2 cos (/ 3/2) sin (/ 3/2), -1 / 2-sin (/ 3/2) cos (/ 3/2). (58,8) Для любого значения j функция φjm имеет вид Элементы ранга 2 j симметричного ковариантного спиннера Мул (57,6).
Матрица преобразования спиновых компонентов раны ha 2 j — произведение 2 j матрицы Z ^ 1/2) г) матричный индекс (58.7) просто Расположить в порядке, соответствующем умножению столбца матрицы Функции в символьных строках (58,7) r / jjm = (^ -Z) ^) м-во Согласно записи (56.13). 272, р и н гл. VIII Действует на один из спинорных индексов.
вперемежку Вернитесь к жене и работайте снова и получите матрицу Преобразовать последний в форму f t ‘D) = (5 8,9) А функция d ^ jj ((3) дается в формуле1) (J + m ‘)! Q ‘-m’)! j 1/2 / p \ t ‘+ t x (J + m) \ (j-то)! _ V 2 / (./3\w~w^im ‘-m, m’ + m) / X V 2 / i ‘m’ A008 / 3) — (58,10) где P ia, b) (cos / 3) = ^ j- (l-cos / 3) a (l + cos f3) до bx x (- * — W l-cos / 3) a + n (l + cos / 3) 6 + n] (58.11) Vd cos / 3 J Так называемый полином Якобиана 2). Пожалуйста, обратите внимание P ^ b) {~ cos / 3) = (-l) nP ^ ‘a) (cos / 3). (58.12) (J), Функции d ^ и m имеют много симметричных свойств.
- Мы могли видеть из уравнений (58.11) и (58.12) Легко получить непосредственно из определения как коэффи Цент вращения преобразования. Матрица как матрица преобразования вращения Унитарное. Потому что это противоположность вращения (Ce, / 3, 7), есть вращение (-7, — / 3, -a), затем фактический мат Рица отношения отсюда = д м л (П) — (58-13) г) Выполнение расчета описано в книге: А. Р. Эдмондс.
угол Мама Энтам из квантовой механики. Принстон, 1957 (см. Также перевод статьи) Определения Согласно (58.9) и (58.10) разделение функций D ^} имеет вид Эдмондс переупорядочивает и 7 и резервы (это Подход) и от того, что также было принято в статье путем изменения знака всех углов. 2) Связь между этими многочленами и гипергеометрическими рядами Ла (е. 1 1)). d (j), W) = t’t V) § 58 Opera Net Effin X VRA Schune Y 273
Тот же автор в сборнике: ядерная деформация. -М. : IL, 1958). Людмила Фирмаль
Кроме того, равенство <Нм (0) = (0)> (58’14) = (~ 1Y + m5m> m, (58L5) ^ t’m (~ 7T) = (- $ m ‘, -m, t, t (0) = Sm’m. Для j = 1/2 они очевидны из (58.8) Произвольное j ясно из метода построения выше. Матрица преобразования. Поверните угол tg- / 3 дважды подряд Включите угол TG и / 3. dm’mfa- / 5) = = (-1 м » Или использовать (58.13) ( «- и») Результат двух поворотов вокруг одной оси не зависит Из последовательности.
Так что вам нужно получить один Тот же результат, поверните / 3 и 7G в обратном порядке. Делая это и сравнивая ответ с (58.16), получим следующее соотношение: = (-1) м’-м ^ 1. , N, (/ 3). (58.17) Из (58.17), (58.14) и (58.13) <£ L (α = (-1Γ ‘-1´ (/ 3) = (-1Г’ «?? (- / 3) — (58,18) Основано на (58.13) — (58.18) Симметрия полной функции D ^ Jm. Пожалуйста, обратите внимание В частности, представление комплексных сопряженных функций *> й>.
0, 7) = = (-1 T ‘- ”1>” ,, _ m (a, / 3, 7). (58.19) С математической точки зрения матрица дает унитарную Неприводимое представление групп вращений с размерностями 2 j + 1 (см. §98 ниже). Это сразу означает орто отношения Диагональ и нормализация / (58.20) Где duj = sin / 3 da d / 3 dj. Функция ортогональности с индексами m и m! предложение Коэффициент exp {r (ta + m! 7)}.
Ортогональность j связан с функцией d ^ ,, (7). 7 (l) (a \ n) (a \ ± — 1. И nх. / (RU (ШиУ (0) — „, 1 а. 2 2j \ + 1 (58,21) Наконец, для справки, вот выражение для функции d ^, m Некоторые конкретные значения параметров. для j = 1 dt’t {1 (/?) = v / нет т / 1 0-1 1 я (l + cos / 3) 1 ~ ^ = Грех / 3 V2 ^ (1 — кос / 3), 1 0 —— грех / 3 V2 я (l-c o s / 3) cos / 3 -Грех / 3 л / 2 7 1 -1 ^ (1 + cos / 3). (58.22) В целом j = я и м! = 0 Уравнения (58.10) и (58.11) О m = (-1 g <& Φ) = (-1) m \ / f i i | p ‘’ ”(co s ‘3)’ <5 8 -23)
Происхождение этой формулы легко проследить по оригиналу Определение (58.7). Связать значения функций (58.7) правая сторона, вверх относительно оси zf (если j = I) Ylm, (nz,) = о. (58.24) Функция ‘ipjm слева является сферической функцией Сферический угол cp = a от Y / W (/ 3, a), 0 = 1 в направлении оси z 0/3. Подставляя (58.24) в (58.7) Гг (/ 3,)) = (58,25) Это эквивалентно (58.23). § 59H A T T I H N A Y P O L I R I Z A C I Y A P A T I C 275 Наконец, дайте максимально возможное выражение функции Индекс м, м! Любое возможное значение \ 4 1 (/ 5) = (-1 = G (2 i V I 1/2 / # V + m / v \ e ~ t =. 7 (j —— + m ———-)! (Дж-мг (соз) (грех)! J V 2 / V 2 / -). 58,26
Смотрите также:
| Спиноры | Частичная поляризация частиц |
| Волновые функции частиц с произвольным спином | Обращение времени и теорема Крамерса |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

