Задача №22.
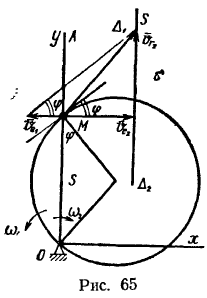
Окружность радиуса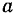 
(рис. 65) вращается в своей плоскости вокруг своей неподвижной точки 
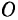с постоянной угловой скоростью 
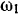против часовой стрелки. Стержень 
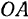вращается в той же плоскости вокруг точки 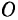с постоянной угловой скоростью 
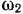по часовой стрелке. На стержень и на окружность надето колечко 
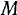. Определить скорость и ускорение колечка в зависимости от ее-личины угла 
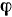, который образует радиус окружности со стержнем.
Решение:
Определим сначала скорости. В качестве подвижной системы координат выберем систему осей, неизменно связанную со стержнем. Тогда для переносной скорости получим следующее значение:
Вектор относительной скорости точки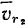 
в этой системе направлен вдоль стержня, а потому и конец вектора абсолютной скорости точки лежит на прямой 
, параллельной стержню и проходящей через конец вектора, -переносной скорости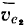 
.
Выберем теперь в качестве подвижной системы координат систему осей, неизменно связанную с окружностью. Тогда переносная скорость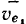 
по величине будет равна
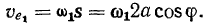
Вектор относительной скорости будет направлен по касательной к окружности и, следовательно, конец вектора абсолютной скорости точки 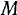лежит на прямой 
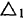, параллельной касательной к окружности и проходящей через конец вектора 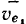. Нетрудно видеть, что прямые 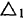и 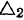.пересекаются в точке 
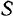, а потому конец вектора абсолютной скорости точки 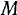будет находиться в той же точке 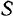. Теперь нетрудно определить и величину скорости точки 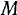(см. рис. 65):
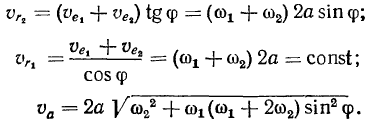
Перейдем к определению ускорений. В системе осей, неизменно связанной с окружностью, материальная точка движется по окружности с постоянной -по величине скоростью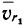 
, а потому и относительное ускорение точки в этой системе отсчета по величине равно
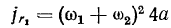
и направлено к центру окружности. Переносное ускорение точки в этой системе координат равно
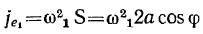
и направлено к точке 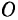. Добавочное ускорение по величине равно
и направлено от центра окружности. Проектируя эти составляющие ускорения на оси 
и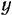 
, получим:
Если в качестве подвижной системы координат выбрать систему осей, связанную со стержнем, то, как нетрудно видеть, будем иметь:
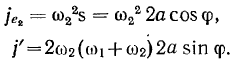
А так как относительное движение в этой системе осей является -прямолинейным движением, то для относительного ускорения получим следующее выражение:
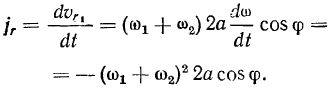
Для проекций ускорения на оси , 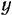получим те же значения:
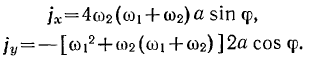
Формулы Ривальса для определения ускорений точек твердого тела значительно упрощаются при рассмотрении плоского движения твердого тела. В плоском движении вектор мгновенной угловой скорости вращения твердого тела может изменяться только по величине и не меняется по направлению. А это значит, что вектор углового ускорения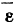 
и вектор мгновенной угловой скорости 
становятся коллинеарными векторами. Благодаря этому формулы принимают особенно наглядный вид. Формулы значительно упрощаются, если за полюс выбрать ту точку твердого тела, которая в данный момент совпадает с положением мгновенного центра вращения твердого тела. Тогда будем иметь
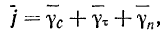
где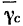 
— ускорение точки твердого тела, совпадающей в данный момент с мгновенным центром вращения, причем
где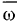 
— мгновенная угловая скорость вращения твердого тела, 
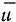— скорость движения мгновенного центра вращения.
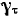и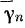 
— соответственно касательная и нормальная составляющие ускорения точки 
тела при вращении последнего вокруг мгновенного центра вращения. Таким образом, если через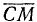 
обозначить расстояние от мгновенного центра вращения до точки ускорение которой определяется, то:
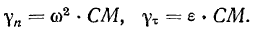
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
