Задача №61.
Окружность радиуса 
, плоскость которой вертикальна, вращается вокруг своего вертикального неподвижного диаметра с постоянной по величине угловой скоростью 
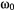. По окружности может свободно скользить тяжелая материальная точка массы 
. Определить положение относительного равновесия материальной точки и найти период малых колебаний точки около положения устойчивого равновесия.
Решение:
Движение точки определяется относительно вращающейся окружности, поэтому целесообразно подвижную систему отсчета связать с окружностью. Выберем начало подвижной системы координат в центре окружности, ось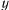 
направим вертикально вверх, а за ось 
примем горизонтальный диаметр окружности. В этой системе движение точки будет определяться двумя силами: силой тяжести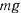 
и силой Кориолиса 
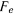от переносного ускорения, величина которой равна 
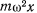и которая направлена от оси вращения. Сила Кориолиса от добавочного ускорения ортогональна к траектории точки и не влияет на характер движения точки.Сила тяжести и сила Кориолиса 
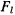допускают существование силовой функции
Если ввести угол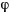 
, определяющий отклонение точки от вертикального диаметра (начало отсчета в нижней точке), то силовую функцию можно будет записать в виде
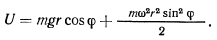
В положении равновесия
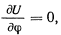
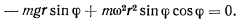
Отсюда имеем два решения, определяющих положение равновесия точки,
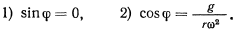
Последнее возможно только тогда, когда
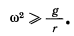
Если
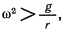
то в нижнем положении
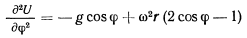
будет величиной положительной, а потому это положение равновесия будет неустойчивым. В положении, где
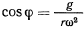
будем иметь
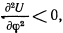
а потому это положение устойчиво. Для определения периода колебаний точки около положения равновесия обратимся сначала к интегралу живых сил
Дифференцируя это уравнение по времени, получим
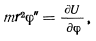
или, раскладывая
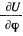
в окрестности положения равновесия по малым значениям
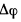
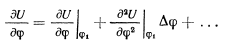
и ограничиваясь малыми членами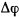 
первого порядка (в положении 
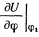равновесия — обращается в нуль), будем иметь
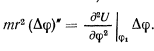
Это линейное дифференциальное уравнение в случае, когда
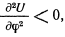
имеет периодическое решение с периодом
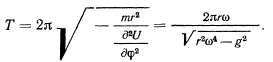
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
