Окружность радиуса катится без скольжения по неподвижной окружности радиуса

Задача №24.

Окружность радиуса 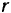катится без скольжения по неподвижной окружности радиуса 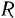так, что скорость ее центра остается постоянной по величине и равна 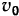во все время движения. Определить ускорение точки 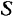окружности, совпадающей в данный момент с положением мгновенного центра вращения, и ускорение точки 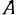, расположенной на противоположном конце диаметра, проходящего через точку .

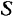Решение:

Так как мгновенный центр вращения находится в точке 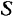, то мгновенная угловая скорость 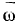будет по величине равна

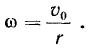
С другой стороны, точка 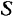все время находится на прямой, соединяющей центры окружностей. Поэтому скорость 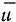движения мгновенного центра вращения определяется из условия

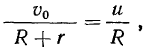
то есть

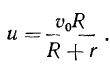
Тогда ускорение точки 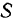твердого тела имеет вид

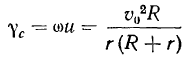
и направлено к центру движущейся окружности.

Нетрудно видеть, что угловое ускорение 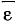будет равно нулю во все время движения, так как вектор мгновенной угловой скорости вращения остается во все время движения постоянным и по величине, и по направлению. Поэтому будет равна нулю и составляюща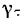я . Для 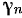получим следующее значение:

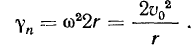
Ускорение точки 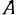определится из равенства

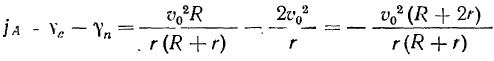
и будет направлено к центру подвижной окружности.

Затруднения, возникающие при определении ускорения точки твердого тела в плоскопараллельном движении, и связанные с определением величины вектора 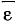, иногда могут быть устранены при рассмотрении проекций ускорения точки на различные оси координат. Рассмотрим следующую задачу.

Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Решение задач по теоретической механике

Возможно эти дополнительные задачи вам будут полезны:

Задача №22. Окружность радиуса (рис. 65) вращается в своей плоскости вокруг своей неподвижной точки с постоянной угловой скоростью против часовой стрелки. Стержень вращается в той же плоскости вокруг точки с постоянной угловой скоростью по часовой стрелке. На стержень и на окружность надето колечко . Определить скорость и ускорение колечка в зависимости от ее-личины угла , который образует радиус окружности со стержнем.

Задача №23. Палочка скользит своим концом по окружности радиуса и проходит через точку этой окружности. Определить ускорение точки палочки, рас-положенной на расстоянии от конца , если точка движется с постоянной по величине скоростью (рис. 66).

Задача №25. Полый цилиндр радиуса вращается вокруг своей неподвижной оси симметрии с постоянной угловой скоростью . По внутренней поверхности этого цилиндра катится без скольжения другой цилиндр радиуса с постоянной относительной угловой скоростью (как показано на рис. 67). Определить ускорение точки малого цилиндра, совпадающей в рассматриваемый момент времени с осью большого.

Задача №26. Прямой круговой конус II с углом при вершине катится без скольжения по внешней стороне неподвижного конуса I с углом при вершине . При этом ось симметрии подвижного конуса вращается вокруг оси симметрии неподвижного конуса с постоянной скоростью угловой . Определить абсолютное ускорение самой верхней точки М основания подвижного конуса.