Пример решения задачи №14.
Охотник стреляет в птицу, которая находится в момент выстрела на расстоянии L = 30 м от него. Выстрел производится в направлении, перпендикулярном траектории полета птицы. Скорость птицы, летящей горизонтально,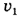 
= 15 м/с, скорость дроби 
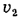= 375 м/с. Какой путь S пролетит птица с момента выстрела до момента, когда в нее попадет дробь?
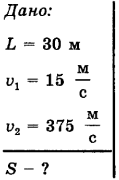
Решение:
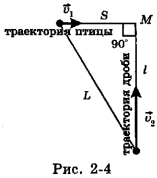
Здесь надо понять, что время t, за которое бедная птица пролетит свой последний путь, и время полета дроби от дула ружья до птицы одно и то же. Это время t нам не дано и не спрашивается в условии задачи, но оно одинаково, значит, этот факт мы должны использовать в решении. Выполним рисунок, на котором обозначим отрезки L и S (рис. 2-4).
Путь, который пролетит дробь, согласно теореме Пифагора
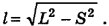
Из уравнений равномерного движения определим время t, за которое птица пролетит расстояние S, а дробь — расстояние l:
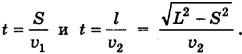
Поскольку левые части этих равенств одинаковы, приравняем их правые части:
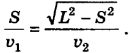
Нам осталось решить это уравнение относительно S, ведь остальные величины нам известны. Для начала возведем обе части этого равенства в квадрат, ведь справа искомая величина S стоит под корнем:
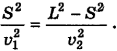
Теперь воспользуемся правилом пропорции, после чего перенесем все члены, содержащие S, в одну сторону равенства, а члены, не содержащие S, в другую, вынесем S за скобки и определим. Приступим:
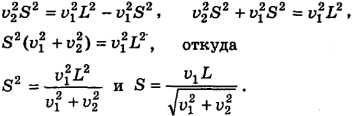
Задача в общем виде решена. Проверьте самостоятельно размерность полученной величины. Должен получиться метр.
Произведем вычисления:
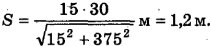
Ответ: S = 1,2 м.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
