Последовательность {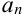
} называется ограниченной, если существуют числа 
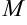и 
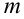такие, что для любого номера 
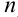имеет место неравенство: 
.
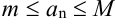Геометрически ограниченность последовательности {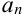} означает существование отрезка 
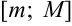, на котором помещены все члены этой последовательности. Одновременно заметим, что для неограниченной последовательности {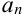} такого отрезка 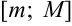, которому принадлежат все члены 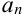, не существуют.
Так, последовательность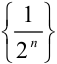 
из примера 8.1 ограничена, т.к. существует 
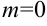и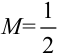 
, такие, что 
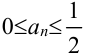. Геометрически все элементы последовательности 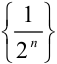принадлежат промежутку 
.
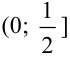Последовательность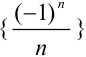 
из примера 8.3 также ограничена, 
.
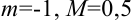Последовательность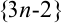 
из примера 8.2 не ограничена, т.к. не существует числа 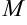, которое бы ограничивало последовательность сверху.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие числовой последовательности. |
| Монотонные последовательности. |
| Предел последовательности. Свойства предела. |
| Бесконечно малые и бесконечно большие последовательности. |
