Односторонняя непрерывность. Точки разрыва

Односторонняя непрерывность. Точки разрыва

• Определим функцию f (x) хотя бы справа (Слева) Точка полукруг, номер линии € R. Определение 0.5 функция} (х) называется Если есть в этой точке, продолжайте направо в точке а Является ли последний правый край функции и соответствует ее значению / (А), то есть (W / (*) = f (b + 0) € E) n (f (a + 0) = f (b)). (9,13) x —►o + U Аналогично, определите непрерывную функцию слева Как функция, укажите (3 lim / (x) = / (e-0) € R) A (/ (e-0) = / (a)). (9,14) x —►o- и Если функция определена с интервалом [a, 6] Для граничных точек А и 6 Правая непрерывность в точке А или слева в точке А функции 6.

Непрерывность функций во внутренних точках Разрыв эквивалентен непрерывности функции в таких точках (см. Теорему 7.1). Точки, где функция продолжается, называются точками Непрерывность этой функции. Точка непрерывности Функция f (x) должна удовлетворять всем следующим условиям: 1) Функция определяется точкой а и ее частью Окружение; 2) В то время существуют ограничения в одну сторону И они конечны. 3) ограничение односторонней функции в точке а По совпадению, т.е. -0) = / (a ​​+ 0); 4) соответствуют одностороннему ограничению функции Значение функции в этой точке, Да-0) = f (a + 0) = f (a). (9,15)

Потому что есть некоторые ограничения, левый и правый Равен существованию левого и правого пределов На данный момент Людмила Фирмаль

Определение 9.6. Несмежные функции В точке a∈R эта точка называется разрывом, Точка А является точкой останова для этой функции. Говоря о точке a как о точке останова, примите это. Дело в любом маленьком соседстве Из области определения функции f (x), отличной от Точка А согласно определению 5.10 является областью ограничения. Определение этой функции). Такие требования, а не баллы Исключает возможность того, что функция f (x) определена, В частности, или в области с, или Подкрестность этой точки или перфорированная окрестность Или, наконец, в проколотом соседе. Сравнение между определением 9.6 и его предшественником Условие непрерывности условия 1-4 в какой-то момент можно увидеть

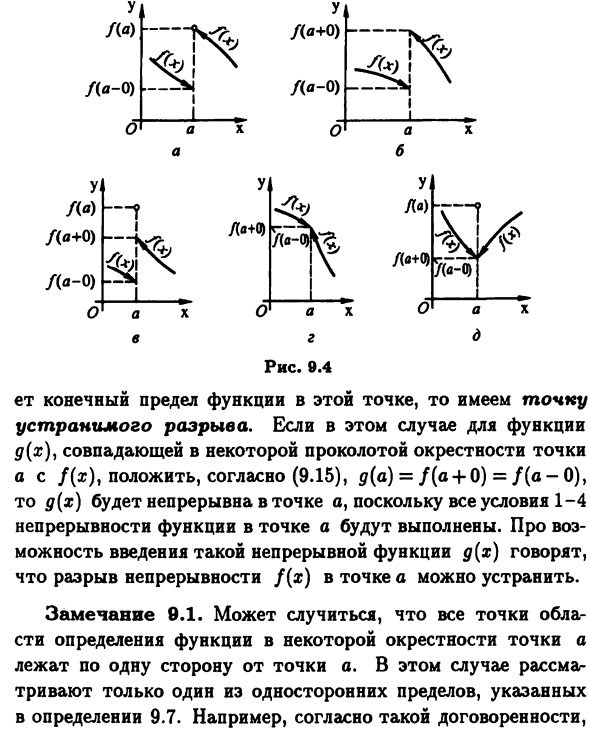
При каких обстоятельствах функция становится прерывистой, или Как говорится, функция ломается в точке а. Определение 9.7. Первый вид точки останова Разрыв функции вызова Оба являются односторонними ограничениями этой функции и являются конечными. Так что для первого типа точки останова, Как минимум условие 2 непрерывности функции в этой точке (рисунок 9.4). Разница / (a ​​+ 0) — / (a-0) конечна и называется скачком О функциях в первом типе точек останова и функций Иногда говорят, что она совершила настоящий прыжок. бели Скачок равен нулю (см. Руководство на рисунке 9.4). В точке А Также есть точка, если непрерывность функции — это условие 3, и, таким образом, существует конечный предел функции в этой точке. Одноразовый разрыв. Функция луч в этом случае d (x)

• Совпадение вблизи точки, где отверстие открыто И c / (x), согласно (9.15), g (a) = f (a + 0) = f (o-0), Поскольку все условия с 1 по 4 выполнены, g (x) непрерывна с a. Непрерывность функции a выполняется. о О возможности введения такой непрерывной функции g (x) говорит Зазор непрерывности f (x) в точке a можно удалить. Примечания 9.1. Все точки могут возникнуть Функциональная область рядом Он лежит на одной стороне точки а. В этом случае Рассмотрим только одно из показанных односторонних ограничений. Определение 9.7. Например, согласно этой договоренности: Точка x = 0 в принципе не называется точкой останова Функция y = y / xy говорит, что эта функция непрерывна в данном Укажите направо. Пример 9.5 Функция q (x) = (sin i) / i Точка а; = 0, но из (7.36), учитывая теорему 7.1, <j (+0) =

= < Эта особенность. Определить функцию g (x) по условию (9.15) Установите q (0) = 1 и напишите ■ { _] § ЦР Приа ^ О, х = О Л -1 Рисунок 9.5 Тогда функция g (x) Непрерывный в x = 0 (Рисунок 9.5). # Все точки останова Ссылка на функцию, которая не является первым типом точки останова Второй вид точки останова. 9.7 Рассмотрим определение точек Сформулируем первый тип разрыва, следующее определение.

7 (-0) = 1. Таким образом, x = 0 — точка удаляемой щели. Людмила Фирмаль

Определение 0.8. Тип 2 точка останова Вызовите хотя бы одну функцию непрерывности Является ли оно бесконечным по одностороннему пределу функции Exist. Пример 9.6 Определение и поиск точки останова Следующая функция персонажа. a * V = Vx — эта функция непрерывна для любого xΦ0. Найти односторонний предел этой функции в точке x = 0. хм- = + оо и хм- = -оо. r-f + O X x — + — 0 X Оба однонаправленных предела не являются конечными.

По определению, 9.8, x = 0 — это второй тип точки останова. (См. Рисунок 7.7). б. y = a1 / * для 0 +0 становится x- + +0 и x -> — 0 y- * + oo. В определении 9.8 x = 0 является точкой останова Тип 2 (см. Рисунок 7.9). с. j / = грех (л / х). В точке х = 0 оба Двустороннее ограничение, а не одностороннее ограничение (см. Пример 7.5). По определению 9.8, x = 0 — это второй тип точки останова. (См. Рисунок 7.10).

Смотрите также:

Предмет математика

Непрерывность функции в точке	Свойства функций, непрерывных в промежутке
Свойства функций, непрерывных в точке	Непрерывность основных элементарных функций