Оглавление:
Односторонние пределы
Определение 3.4. Число А называется правым (левым) пределом функции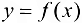 
в точке 
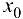, если для любой последовательности 
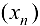, сходящейся к 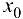, элементы которой больше (меньше) 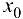, соответствующая последовательность значений функции 
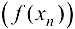сходится к А при 
.
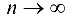Таким образом, определение правого предела:
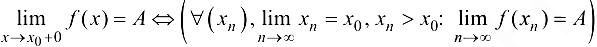
определение левого предела:
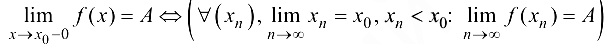
Предел справа обозначается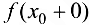 
, предел слева — 
.
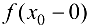Теорема 3.2*. Функция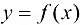 
имеет предел в точке 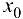тогда и только тогда, когда в этой точке существуют правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции 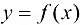в точке .
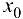Пример 3.3.
Найти односторонние пределы функции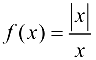 
в х точке 
.
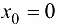Решение:
По определению,
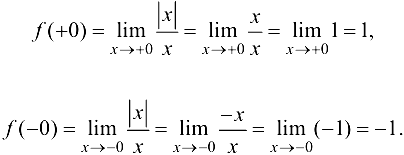
Вывод. Так как односторонние пределы функции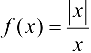 
в точке 
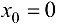существуют, но не равны между собой, то данная функция не имеет предела в этой точке.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
