Оглавление:
Односторонние пределы функций
Если отыскивается предел функции 
при условии, что 
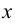стремясь к 
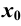, т. е. 
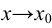, может принимать только такие значения, которые меньше 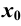, то этот предел, если он существует, называется левосторонним пределом функции . Левосторонний предел функции обозначается символом:
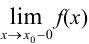или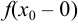 
.
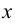Если отыскивается предел функции при условии, что стремясь к 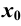, т. е. 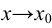, может принимать только такие значения, которые больше 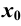, то этот предел, если он существует, называется правосторонним пределом функции . Правосторонний предел функции обозначается символом:
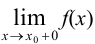или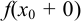 
.
Очевидно, что предел функции при 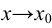существует только тогда, когда существуют и равны между собой её левосторонний и правосторонний пределы, т. е.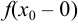 
.
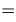
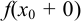Функция называется непрерывной при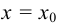 
, если её левосторонний и правосторонний пределы существуют, равны между собой и равны значению функции в этой точке, т. е.
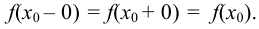
Если это равенство не выполняется, то точка 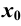является точкой разрыва.
Если существуют левосторонний 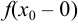и правосторонний 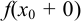пределы функции, но не равны между собой, т. е.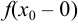 
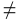
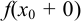, то точка 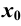называется точкой разрыва первого рода.
Величина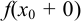 
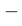
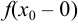называется скачком функции в точке .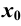
Если в точке 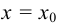не существует левосторонний или правосторонний предел функции или не существуют оба предела одновременно, то эта точка называется точкой разрыва второго рода. Во всех этих случаях функция терпит разрыв второго рода.
Если в точке 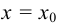функция имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке 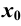, т. е.
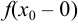
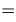
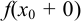
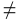
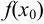, то точка 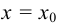называется точкой устранимого разрыва.
Разрыв «устраняется» тем, что полагают 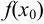равным 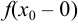и 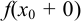, т. е. принимают, что 
.
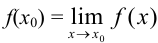Задача №45.
Показать, что функция
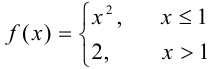
имеет разрыв в точке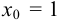 
.
Решение:
При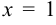 
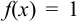. Найдём односторонние пределы функции в точке .
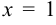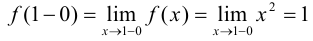
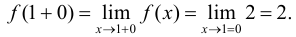
Имеем: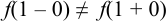 
. Условие непрерывности не выполнено. В точке 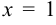функция имеет разрыв. Это точка разрыва первого рода.
Задача №46.
Какого рода разрыв имеет функция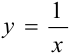 
в точке 
?
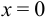Решение:
Функция терпит разрыв в точке 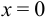. Левосторонний предел функции 
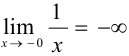. Правосторонний предел функции 
.
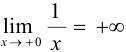Здесь не существует ни предела слева, ни предела справа, а поэтому точка 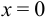— точка разрыва второго рода.
Задача №47.
Непрерывна ли функция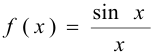 
? Если нет, то в какой точке непрерывна, и какого рода эта точка имеет разрыв?
Решение:
Функция не является непрерывной, так как она неопределена в точке .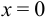
Известно, что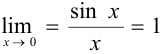 
, т. е. существуют левосторонний и правосторонний пределы и равны 1, но 
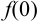— не существует. Если условимся, что при 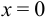функция 
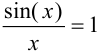, то разрыв будет «устранён». Точка 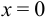является точкой устранимого разрыва, так как 
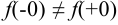и функция в этой точке может быть доопределена так, что можно взять 
.
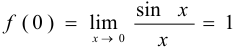Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
