Односторонние пределы функции
В определении предела функции 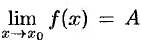 считается, что
считается, что  стремится к
стремится к  любым способом: оставаясь меньшим, чем
любым способом: оставаясь меньшим, чем  (слева от
(слева от  ), большим, чем
), большим, чем  (справа от
(справа от  ), или колеблясь около точки
), или колеблясь около точки  .
.
Бывают случаи, когда способ приближения аргумента  к
к  существенно влияет па значение предела функции. Поэтому вводя понятия односторонних пределов.
существенно влияет па значение предела функции. Поэтому вводя понятия односторонних пределов.
Число 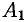 называется пределом функции
называется пределом функции  слева в точке
слева в точке  , если для любого число
, если для любого число 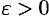 существует число
существует число 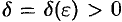 такое, что при
такое, что при 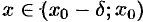 , выполняется неравенство
, выполняется неравенство 
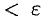 . Предел слева записывают так:
. Предел слева записывают так: 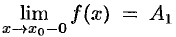 или коротко:
или коротко: 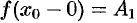 (обозначение Дирихле) (см. рис. 111).
(обозначение Дирихле) (см. рис. 111).
Аналогично определяется предел функции справа, запишем его с помощью символов:
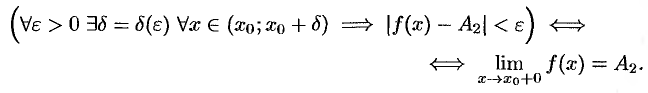
Коротко предел справа обозначают 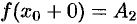 .
.
Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует 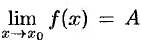 , го существуют и оба односторонних предела, причем
, го существуют и оба односторонних предела, причем 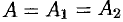 .
.
Справедливо и обратное утверждение: если существуют оба предела 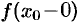 и
и 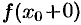 и они равны, то существует предел
и они равны, то существует предел 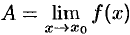 и
и 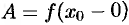 .
.
Если же 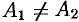 , то
, то 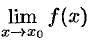 не существует.
не существует.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Числовые последовательности |
| Предел функции в точке |
| Предел функции при х к бесконечности |
| Бесконечно большая функция |

