Односторонние пределы

Односторонние пределы

Односторонние пределы. Если область&находится рядом с a, то » o » в правой части a7 имеет значение x, и определение предела функции, заданного в числах 32 и 33, может быть специализированным, и только значение x> a является limited. In в этом случае предел функции называется пределом функции f (x), поскольку он присутствует и x приближается к правому a (или короткому и правому a).

Для ясности следует брать более крупные масштабы вдоль оси x, что вызывает искажение. Людмила Фирмаль

• М /(х) или/(А + 0). х * а + о ( * ) На рисунках 20 и 21 Понятие предела функции определяется так же, как x приближается к левой стороне (в точке a). Hm /(x) или/(a-0)*). х-а-0 Оба эти ограничения называются односторонними.

• Одно и другое можно рассматривать, если область допускает неограниченное приближение вправо и влево a. It это просто. Чтобы установить существование нормального («двухстороннего») предела (6), необходимо и достаточно, чтобы оба предела были равны и существовали отдельно слева и справа. Тю /(х)=Золотой/(х)= а х * а + 0 х + а-0

Обратите внимание, что хотя оба эти ограничения могут существовать, они не равны. Людмила Фирмаль

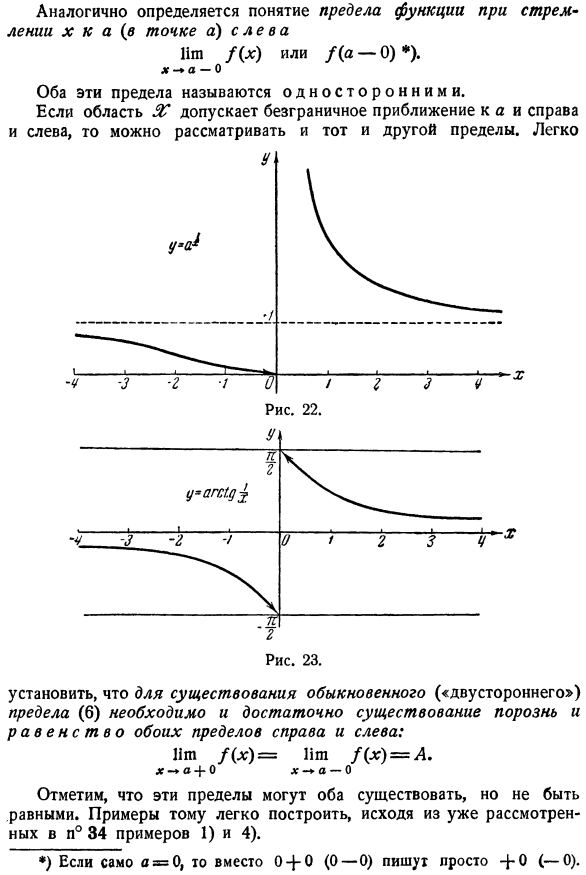
• Этот пример может быть легко построен на основе примеров (34) и (4), уже рассмотренных в разделе 1. •) если a = 0 само по себе, вместо 0 + 0 (0-0), просто напишите+0 (-0). Пример уравнения определяет 2 функции xΦ0 1 A (x)= <*(a> 0, A (x)= ags (e для первого、 А(+ 0)= Хм топор = ПМ, АР =\ ω、 + O 2- 4 ^®> Я Λ(-0)= НХ топор==. Нгн АГ = 0. Слева.—-0 2ОО Второй ж |даже / * (+0) Хм АГС!^ =ППН АГС(§ 2= х--| −0 х г- 4-оо А(-0)= тю ags12 = гв ags1dg =Х -, o х г-ко * График этих функций показан на рисунке. 22 и 23.

Смотрите также:

Решение задач по математическому анализу

Определение предела функции.	Свойства функции от натурального аргумента, имеющей конечный предел.
Другое определение предела функции.	Распространение на случай функции от произвольной переменной.