Оглавление:

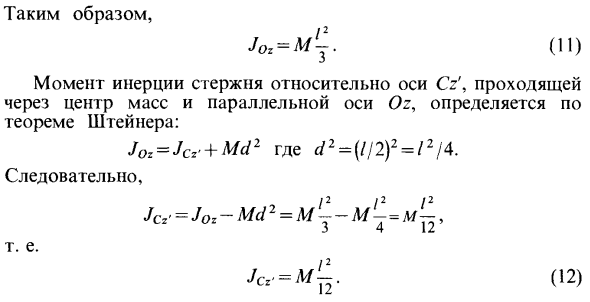

Однородный стержень
- Есть стержень с одинаковой длиной I и массой M (рис. 25). Сориентируйте быка на стержень вдоль оси. Рассчитайте момент инерции стержня относительно оси Oz, которая проходит перпендикулярно от конца стержня к стержню. Согласно определению момента инерции континуума вокруг оси, Рисунок 25 JOl-f x2dm = p j x2dx.
Значения RP для этих векторов считаются положительными, если направление соответствующего вектора соответствует выбранному полупрямому направлению, а отрицательное направление совпадает. Людмила Фирмаль
Поскольку dw = pdx, p = M / l — плотность стержня. При расчете интеграла это выглядит так Вот так JOl = M ^. (11). Момент инерции стержня относительно оси Cz ‘, проходящей через центр тяжести и параллельный оси Oz, определяется по теореме Штейнера. JOl = JCl + Md2, где rf2 = (// 2) 2 = / 2/4 так. Это JCz = m ‘^. (12)
- Поэтому при дальнейшем решении задачи необходимо перейти к рассмотрению равновесия узлов, в которых не действуют две и более неизвестные силы. Усилие в стержне направлено и получено от рассматриваемого узла. Это означает, что стержни 1 и 3 сжаты, а стержни 2 растянуты.
Поэтому шестое уравнение системы, составленное путем решения этой задачи методом кинетостатики, по существу является дифференциальным уравнением для вращения твердых тел вокруг неподвижных осей. Людмила Фирмаль
Введем эти характеристики действия сил на твердые тела и рассмотрим их характеристики. Из определения алгебраического момента силы в некоторой точке следует, что она не зависит от переноса сил вдоль линии ее действия. Если линия действия силы проходит через точку момента, то алгебраический момент силы относительно точки равен нулю.
Смотрите также:
Задачи по теоретической механике
| Теорема о моментах инерции относительно параллельных осей (теорема Штейнера) | Прямоугольная пластина |
| Моменты инерции простейших однородных тел | Круглый диск |

