Задача №43.
Однородный стержень весом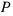 
опирается верхним своим концом на негладкую вертикальную стенку (коэффициент трения равен 
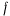), а нижним — на гладкий горизонтальный стол и удерживается в равновесии в вертикальной плоскости при помощи привязанной к его нижнему концу и протянутой по столу веревки, которая затем перекинута через блок и несет на своем свободном конце груз весом 
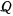. Найти, при каких значениях угла наклона стержня а возможно равновесие системы, а также определить реакции в точках 
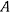и 
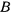(рис. 46).
Решение:
Введем силу реакции в точке 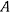, состоящую из двух составляющих: нормальной реакции 
, направленной перпендикулярно к стенке, и касательной составляющей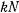 
, направленной вдоль стенки. Будем считать эту составляющую положительной, когда она направлена вверх. После введения такой силы реакции среди возможных перемещений появится поступательное перемещение всей системы в горизонтальном направлении. Рассматривая работу всех сил, действующих на систему на этом возможном перемещении, получим условие для определения равновесия
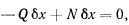
откуда непосредственно следует
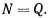
С другой стороны, среди возможных перемещений будет существовать поворот стержня вокруг мгновенного центра вращения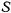 
. Этому возможному перемещению будет соответствовать равенство нулю обобщенной силы, которая определяется как сумма моментов всех сил относительно точки 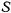. Будем иметь
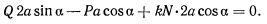
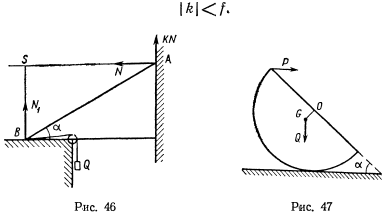
После подстановки сюда значения получим условие равновесия
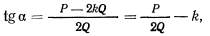
Для определения реакции в точке 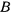освободим точку от связи и введем в рассмотрение силу реакции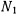 
ортогональную к полу. Среди возможных перемещений стержня появится поступательное перемещение в вертикальном направлении. Подсчитывая работу всех сил, действующих на стержень, на этом возможном перемещении и приравнивая работу нулю, будем иметь
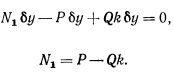
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
