Задача №36.
Однородный стержень 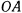 весом
весом 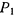 может вращаться на неподвижном шарнире
может вращаться на неподвижном шарнире 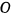 в вертикальной плоскости. Конец
в вертикальной плоскости. Конец 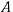 этого стержня соединен шарнирно с другим однородным стержнем
этого стержня соединен шарнирно с другим однородным стержнем 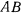 весом
весом 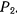 . К концу
. К концу 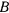 второго стержня приложена горизонтальная сила
второго стержня приложена горизонтальная сила 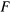 . Найти углы
. Найти углы 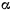 и
и  стержней с горизонтальным направлением при равновесии системы (рис. 29).
стержней с горизонтальным направлением при равновесии системы (рис. 29).
Решение:
Система обладает двумя степенями свободы и углы 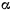 и
и  могут быть выбраны в качестве обобщенных координат. Условия равновесия выразятся в виде уравнений
могут быть выбраны в качестве обобщенных координат. Условия равновесия выразятся в виде уравнений
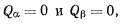
где 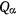 и
и 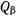 — соответствующие обобщенные силы. Для определения этих обобщенных сил рассмотрим сначала перемещение, при котором изменяется только параметр
— соответствующие обобщенные силы. Для определения этих обобщенных сил рассмотрим сначала перемещение, при котором изменяется только параметр 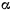 , а угол
, а угол  остается неизменным. Работа, подсчитанная на этом перемещении,
остается неизменным. Работа, подсчитанная на этом перемещении,  откуда обобщенная сила
откуда обобщенная сила
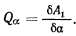
Но выражение элементарной работы имеет вид:
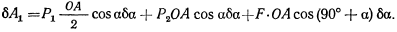
Отсюда, приравнивая 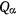 нулю, получаем условие равновесия в виде уравнения
нулю, получаем условие равновесия в виде уравнения
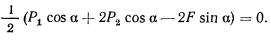
Угол 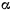 определится теперь равенством
определится теперь равенством
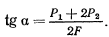
Полагая далее 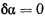 и
и 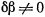 , будем иметь
, будем иметь
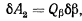
или
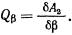
Подсчитывая работу сил на этом возможном перемещении

получим выражение для обобщенной силы
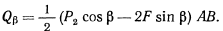
Приравнивая это выражение нулю, получим условие для определения угла  , откуда
, откуда
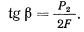
Замечание. В тех случаях, когда возможным перемещением оказывается поступательное перемещение всей системы, обобщенная сила, соответствующая этому возможному перемещению, представляет собой сумму проекций всех активных сил, действующих в направлении возможного поступательного перемещения системы.
Если же возможное перемещение сводится к повороту всей системы (как одного твердого тела) вокруг некоторой неподвижной в пространстве оси, то обобщенная сила, соответствующая этому возможному перемещению, будет представлять собой сумму моментов всех активных сил относительно данной неподвижной в пространстве оси.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

