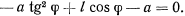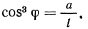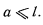Задача №30.
Однородный гладкий стержень 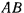 длины
длины 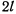 и веса
и веса 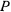 опирается концом на гладкую вертикальную стенку и одной из своих точек лежит на краю
опирается концом на гладкую вертикальную стенку и одной из своих точек лежит на краю 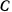 неподвижного стола (рис. 3). Определить угол
неподвижного стола (рис. 3). Определить угол 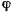 , который образует стержень со столом в поло-женин равновесия, если расстояние от стенки до стола равно
, который образует стержень со столом в поло-женин равновесия, если расстояние от стенки до стола равно 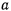 .
.
Решение:
Положение стержня здесь, как и в предыдущей задаче, определяется всего одним параметром — углом 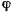 и, следовательно, система имеет одну степень свободы. На стержень действует единственная активная сила — сила тяжести, имеющая вертикальное направление. Подсчитывая работу этой силы на возможном перемещении системы и приравнивая ее нулю, будем иметь
и, следовательно, система имеет одну степень свободы. На стержень действует единственная активная сила — сила тяжести, имеющая вертикальное направление. Подсчитывая работу этой силы на возможном перемещении системы и приравнивая ее нулю, будем иметь
где
Дифференцируя выражение для 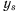 по
по 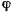 и подставляя результат дифференцирования в уравнение работы, получим
и подставляя результат дифференцирования в уравнение работы, получим
Так как 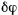 отлично от нуля при произвольном возможном перемещении системы, нулю будет равно выражение, стоящее в скобках. Последнее и представляет собой условие равновесия:
отлично от нуля при произвольном возможном перемещении системы, нулю будет равно выражение, стоящее в скобках. Последнее и представляет собой условие равновесия:
Отсюда следует
Последнее равенство возможно только при выполнении условия
Рассмотрим задачу о равновесии системы с двумя степенями свободы.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №28. Полиспаст (механизм для поднятия тяжестей, состоящий из двух систем блоков, каждый из которых смонтирован в общей обойме и насажен на отдельные оси, как указано на рис. 1) оснащен нитью, один из концов которой прикреплен к неподвижной точке полиспаста, а другой свободен и находится под воздействием некоторой активной силы . Нить последовательно обходит как подвижные, так и неподвижные блоки. К нижнему блоку подвешен груз весом . Определить соотношение величин силы и веса при равновесии системы. |
| Задача №29. Два однородных стержня и , имеющих соответственно длину и вес каждый, могут вращаться в одной вертикальной плоскости: первый — вокруг своей середины ; второй — вокруг шарнира , расположенного на одной вертикали с на расстоянии от точки (рис. 2). Определить положение равновесия системы. |
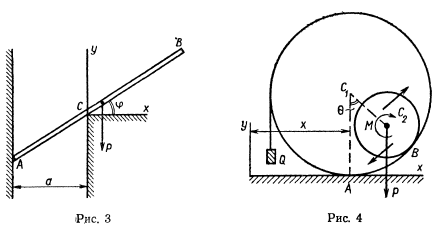
| Задача №31. В полый цилиндр радиуса , способный катиться без скольжения по горизонтальной плоскости, вложен другой цилиндр радиуса и веса (рис. 4). На малый цилиндр, кроме силы тяжести, действует еще пара сил, расположенная в плоскости чертежа, с моментом . На полый цилиндр намотана нить, которая на своем свободном конце несет груз веса . Полагая поверхности цилиндров достаточно шероховатыми (чтобы не было скольжения), найти положение равновесия системы и определить, при какой зависимости между данными силами это равновесие возможно. |
| Задача №32. Палочка длины и веса опирается концом на наклонную плоскость , образующую угол с горизонталью, а в точке лежит на опоре (рис. 5). Определить угол , который палочка образует с горизонталью при равновесии. Размеры и расположение палочки и опоры указаны на чертеже. |

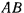 длины
длины 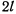 и веса
и веса 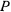 опирается концом на гладкую вертикальную стенку и одной из своих точек лежит на краю
опирается концом на гладкую вертикальную стенку и одной из своих точек лежит на краю 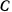 неподвижного стола (рис. 3). Определить угол
неподвижного стола (рис. 3). Определить угол 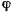 , который образует стержень со столом в поло-женин равновесия, если расстояние от стенки до стола равно
, который образует стержень со столом в поло-женин равновесия, если расстояние от стенки до стола равно 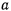 .
.
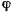 и, следовательно, система имеет одну степень свободы. На стержень действует единственная активная сила — сила тяжести, имеющая вертикальное направление. Подсчитывая работу этой силы на возможном перемещении системы и приравнивая ее нулю, будем иметь
и, следовательно, система имеет одну степень свободы. На стержень действует единственная активная сила — сила тяжести, имеющая вертикальное направление. Подсчитывая работу этой силы на возможном перемещении системы и приравнивая ее нулю, будем иметь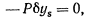
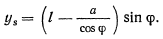
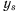 по
по 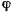 и подставляя результат дифференцирования в уравнение работы, получим
и подставляя результат дифференцирования в уравнение работы, получим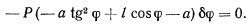
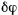 отлично от нуля при произвольном возможном перемещении системы, нулю будет равно выражение, стоящее в скобках. Последнее и представляет собой условие равновесия:
отлично от нуля при произвольном возможном перемещении системы, нулю будет равно выражение, стоящее в скобках. Последнее и представляет собой условие равновесия: