Пример решения задачи №69.
Однородный диск радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно плоскости диска. Зависимость угла поворота диска от времени дается уравнением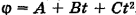 
, где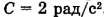 
. Вращению диска противодействует тормозящий момент сил трения 
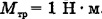. Определить величину касательной силы F, приложенной к ободу диска.
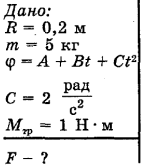
Решение:
Касательная сила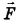 
, приложенная к ободу диска, создает вращающий момент сил 
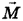, который по определению момента силы равен произведению величины этой силы F и ее плеча. Плечом силы F в нашем случае является радиус диска, поэтому 
.
Вращающему моменту силы 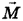противодействует момент сил трения 
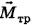. Согласно основному уравнению динамики вращательного движения произведение момента инерции J диска и его углового ускорения 
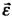равно векторной сумме моментов сил, приложенных к диску относительно центра вращения 0 (рис. 16-8):
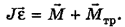
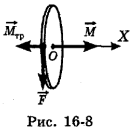
Поскольку векторы моментов сил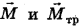 
антинаправлены (в чем несложно убедиться, используя правило правого винта), то в проекциях на ось ОХ этот закон примет вид
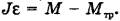
Момент инерции диска относительно оси вращения определяется по формуле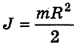 
.
Угловое ускорение диска найдем как вторую производную угла поворота диска по времени:
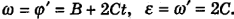
Подставив правые части (1), (3) и (4) в (2), мы получим уравнение, в котором будет только одна неизвестная -искомая сила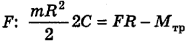 
.
Отсюда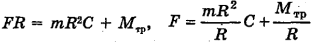 
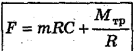
Подставим числа и произведем вычисления:
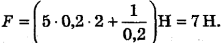
Ответ: F = 7 Н.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
