Оглавление:
Многочлен 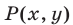 называют однородным многочленом степени
называют однородным многочленом степени 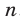 , если
, если 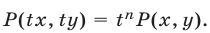 Например, многочлен
Например, многочлен 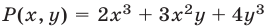 является однородным многочленом третьей степени. Система двух уравнений с двумя неизвестными вида
является однородным многочленом третьей степени. Система двух уравнений с двумя неизвестными вида
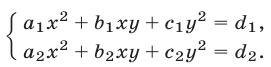
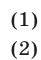
является однородной, так как левые части уравнений (1) и (2) представляют собой однородные многочлены второй степени.
Рассмотрим сначала пример однородной системы, в которой одно из чисел 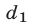 ,
, 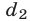 равно нулю.
равно нулю.
Пример №171.
Решить систему уравнений
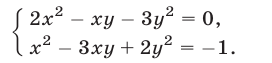
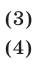
Решение:
Если положить 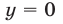 , то из уравнения (3) находим
, то из уравнения (3) находим 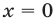 . Но пара чисел
. Но пара чисел 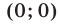 не удовлетворяет уравнению (4). Поэтому,
не удовлетворяет уравнению (4). Поэтому,
разделив обе части уравнения (3) на 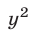 , получим уравнение
, получим уравнение
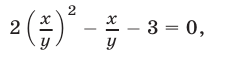
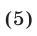
которое вместе с уравнением (4) образует систему, равносильную исходной. Из уравнения (5) находим, что 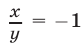 или
или 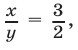 т. е.
т. е. 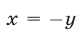 или
или 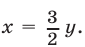 Поэтому исходная система равносильна совокупности следующих систем:
Поэтому исходная система равносильна совокупности следующих систем:
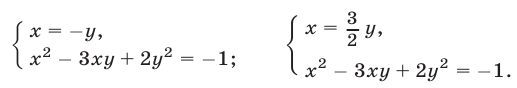
Из первой системы получаем уравнение 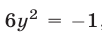 , не имеющее действительных корней.
, не имеющее действительных корней.
Решив вторую систему, находим два решения 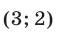 и
и 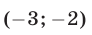 исходной системы.
исходной системы.
Ответ. 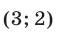 ,
, 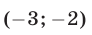 .
.
Рассмотрим теперь однородную систему вида (1), (2), в которой 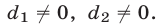
Пример №172.
Решить систему уравнений
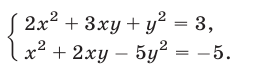
Решение:
Первый способ. Сведем эту систему к системе того же вида, у которой одно из чисел 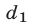 ,
, 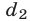 равно нулю. Умножим первое уравнение на
равно нулю. Умножим первое уравнение на 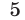 , а второе на
, а второе на 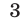 и сложим полученные уравнения.
и сложим полученные уравнения.
В результате придем к уравнению
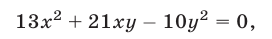
которое вместе в первым уравнением образует систему, равносильную данной. Как и в предыдущем примере, пара чисел 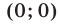 не является решением исходной системы. Поэтому последнее уравнение равносильно уравнению
не является решением исходной системы. Поэтому последнее уравнение равносильно уравнению
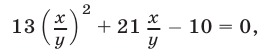
откуда 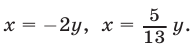
Если 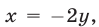 то из первого уравнения исходной системы получаем
то из первого уравнения исходной системы получаем 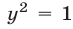 , откуда
, откуда 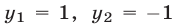 и, следовательно,
и, следовательно, 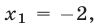
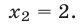
х2 = 2.
Аналогично, если 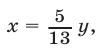 то
то 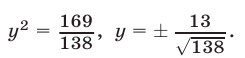
Ответ. 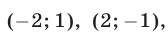
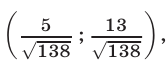
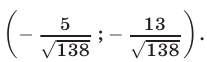
Второй способ. Разделим почленно уравнения данной системы, а затем разделим числитель и знаменатель в левой части полученного уравнения на 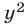 . В результате придем к уравнению
. В результате придем к уравнению
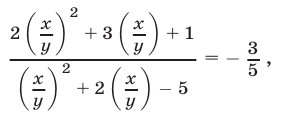
которое можно записать в виде
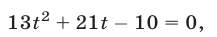
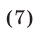
где 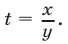 Уравнение (7) совпадает с уравнением (6).
Уравнение (7) совпадает с уравнением (6).
Рассмотрим теперь систему, у которой левые части уравнений являются однородными многочленами третьей степени.
Пример №173.
Решить систему уравнений
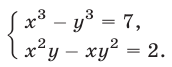
Решение:
Разложив левые части уравнений на множители, запишем систему в виде
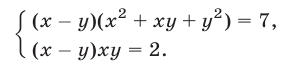
Разделив уравнения этой системы почленно, получим уравнение
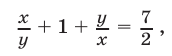
которое вместе с первым уравнением исходной системы образует систему, равносильную исходной.
Полагая 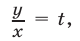 получаем
получаем 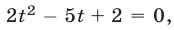 откуда
откуда 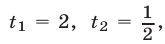 т. е.
т. е. 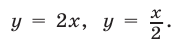 Если
Если 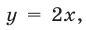 то из первого уравнения находим
то из первого уравнения находим 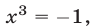 откуда
откуда 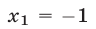 (другие корни уравнения
(другие корни уравнения 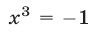 не являются действительными) и поэтому
не являются действительными) и поэтому 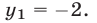
Аналогично, если 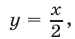 то
то 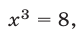 откуда
откуда 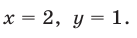
Ответ.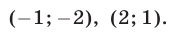
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

