Оглавление:
Однородные дифференциальные уравнения
К уравнению с разделяющимися переменными приводятся одно родные ДУ первого порядка.
Функция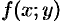 
называется однородной функцией 
-го порядка (измерения), если при умножении каждого ее аргумента на произвольный множитель 
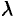вся функция умножится на 
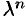, т. е.
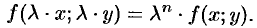
Например, функция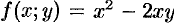 
есть однородная функция второго порядка, поскольку
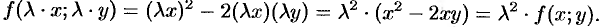
Дифференциальное уравнение
называется однородным, если функция 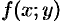есть однородная функция нулевого порядка.
Покажем, что однородное ДУ (48.7) можно записать в виде
Если 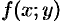однородная функция нулевого порядка, то, по определению, 
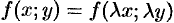. Положив 
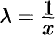, получаем:
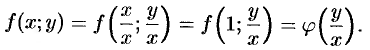
Однороднее уравнение (48.8) преобразуется в уравнение с раздел:
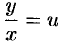или, что то же самое, 
Действительно, подставив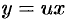 
и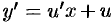 
в уравнение (48.8), получаем 
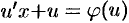или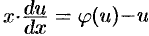 
,т. е. уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем 
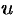на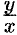 
. Получим общее решение (интеграл) исходного уравнения.
Однородное уравнение част о задается в дифференциальной форме:
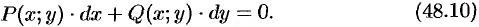
ДУ (48.10) будет однородным, если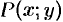 
и 
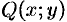— однородные функции одинакового порядка.
Переписав уравнение (48.10) в виде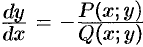 
и применив в правой части рассмотренное выше преобразование, получим уравнение 
.
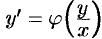При интегрировании уравнений вида (48.10) нет необходимости предварительно приводить их (но можно) к виду (48.8): подстановка (48.9) сразу преобразует уравнение (48.10) в уравнение с разделяющимися переменными.
Пример №48.6.
Найти общий интеграл уравнения
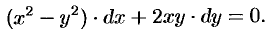
Решение:
Данное уравнение однородное, т. к. функции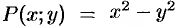 
и 
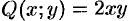— однородные функции второго порядка.
Положим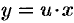 
. Тогдаdy 
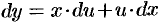. Подставляем в исходное уравнение:
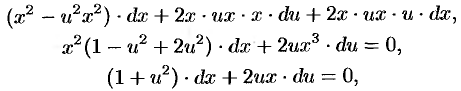
последнее — уравнение с разделяющимися переменными. Делим переменные
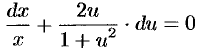
и интегрируем
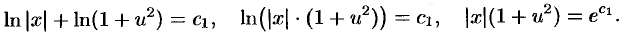
Обозначим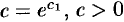 
. Тогда
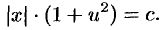
Заменяя 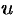на 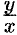получаем: 
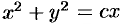— общий интеграл исходного уравнения.
Отметим, что данное уравнение можно было сначала привести виду (48.8):
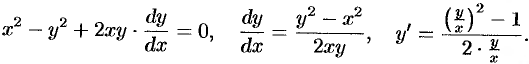
Затем положить 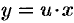, тогда 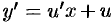и т. д.
Замечание. Уравнение вида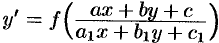 
, 
, 
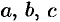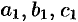— числа, приводится к однородному или с разделяющимися переменными. Для этого вводят новые переменные 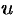и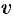 
, положив 
, 
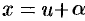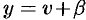, где 
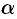и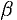 
— числа. Их подбирают так, чтобы уравнение стало однородным.
Дополнительный пример №48.7.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Задачи, приводящие к дифференциальным уравнениям |
| Уравнения с разделяющимися переменными |
| Линейные уравнения Бернулли |
| Метод вариации произвольных постоянных |
