Контрольная работа Д2.
Однородная горизонтальная платформа (прямоугольная со сторонами 21 и 1), имеющая массу 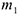 жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси
жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси  с угловой скоростью
с угловой скоростью 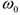 (рис. Д2а). В момент времени
(рис. Д2а). В момент времени 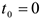 на вал начинает действовать вращающий момент
на вал начинает действовать вращающий момент  , направленный противоположно
, направленный противоположно 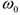 ; одновременно груз
; одновременно груз 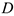 массой
массой 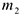 , находящийся в желобе
, находящийся в желобе 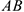 в точке
в точке 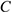 , начинает двигаться по желобу (под действием внутренних сил) по закону
, начинает двигаться по желобу (под действием внутренних сил) по закону 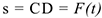 .
.
Дано:
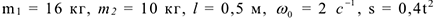
(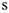 — в метрах;
— в метрах; 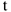 — в секундах),
— в секундах),
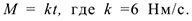
Определить
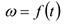
закон изменения угловой скорости платформы.
Решение. Рассмотрим механическую систему, состоящую из платформы и груза 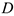 . Для определения
. Для определения 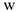 применим теорему об изменении кинетического момента системы относительно оси
применим теорему об изменении кинетического момента системы относительно оси  :
:
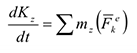
Изобразим действующие на систему внешние силы: силы тяжести 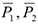 реакции
реакции 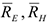 и вращающий момент
и вращающий момент 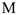 . Так как силы
. Так как силы  и
и 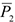 параллельны оси
параллельны оси  , а реакции
, а реакции 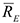 и
и 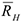 эту ось пересекают, то их моменты относительно оси
эту ось пересекают, то их моменты относительно оси  равны нулю. Тогда, считая для момента положительным направление
равны нулю. Тогда, считая для момента положительным направление 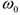 (т. е. против хода часовой стрелки), получим
(т. е. против хода часовой стрелки), получим 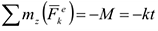 и уравнение (1) примет такой вид:
и уравнение (1) примет такой вид:

Умножая обе части этого уравнения на 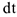 и интегрируя, получим
и интегрируя, получим
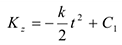
Для рассматриваемой механической системы
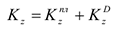
где 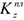 и
и 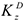 — кинетические моменты платформы и груза
— кинетические моменты платформы и груза 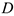 соответственно. Так как платформа вращается вокруг оси
соответственно. Так как платформа вращается вокруг оси  , то
, то 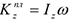 . Значение
. Значение  найдем по теореме Гюйгенса:
найдем по теореме Гюйгенса:
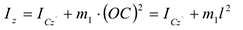
(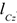 — момент инерции относительно оси
— момент инерции относительно оси 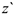 параллельной оси
параллельной оси  и проходящей через центр
и проходящей через центр 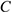 платформы). Но, как известно,
платформы). Но, как известно,
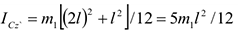
Тогда
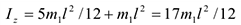
Следовательно,
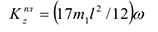
Для определения 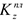 обратимся к рис. Д5, б и рассмотрим движение груза
обратимся к рис. Д5, б и рассмотрим движение груза 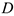 как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси
как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси  переносным движением. Тогда абсолютная скорость груза
переносным движением. Тогда абсолютная скорость груза

Так как груз 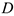 движется по закону
движется по закону
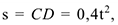
то
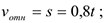
изображаем вектор 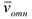 на рис. Д2 б с учетом знака
на рис. Д2 б с учетом знака 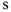 (при
(при 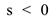 направление
направление 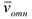 было бы противоположным). Затем, учитывая направление о, изображаем вектор
было бы противоположным). Затем, учитывая направление о, изображаем вектор 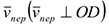 численно
численно 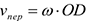 . Тогда, по теореме Вариньона,
. Тогда, по теореме Вариньона,
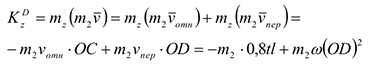
Но на рис. Д2 б видно, что
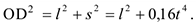
Подставляя эту величину в равенство (6), а затем значения 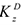 и
и 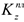 из (б) и (5) в равенство (4), получим с учетом данных задачи
из (б) и (5) в равенство (4), получим с учетом данных задачи
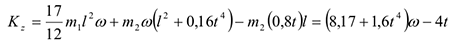
Тогда уравнение (3), где 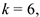 примет вид
примет вид
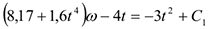
Постоянную интегрирования определяем по начальным условиям: при 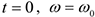 . Получим
. Получим 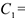
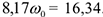 . При этом значении
. При этом значении 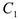 из уравнения (8) находим искомую зависимость
из уравнения (8) находим искомую зависимость 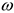 от
от 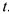 . Ответ:
. Ответ: 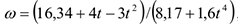 , где
, где 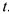 — в секундах,
— в секундах, 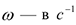 .
.

