Задача №53.
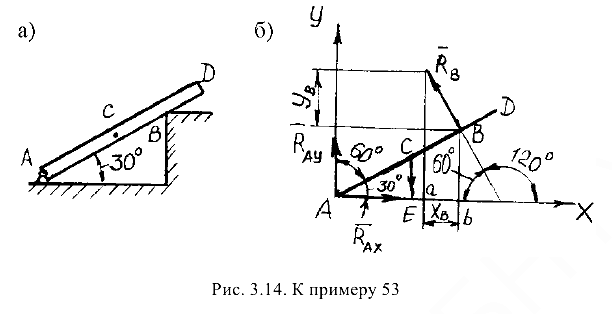
Однородная балка (рис. 3.14, а), сила тяжести которой 2 кН, закреплена в точке 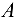 с помощью шарнирно-неподвижной опоры и опирается в точке
с помощью шарнирно-неподвижной опоры и опирается в точке 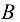 на ребро стены. Найти реакции опор, если
на ребро стены. Найти реакции опор, если
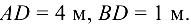
Решение:
На балку действует одна активная сила — сила тяжести. Сила тяжести однородной балки приложена в ее середине (точка 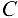 ). Освободим балку от связей, приложив к ней вместо связей силы реакций (рис. 3.14, б). В точке
). Освободим балку от связей, приложив к ней вместо связей силы реакций (рис. 3.14, б). В точке 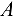 к балке надо приложить неизвестную по модулю и направлению реакцию
к балке надо приложить неизвестную по модулю и направлению реакцию 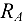 . Разложим ее па две составляющие
. Разложим ее па две составляющие 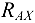 и
и 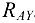 . В точке
. В точке 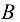 балка опирается па ребро. В таком случае реакция
балка опирается па ребро. В таком случае реакция 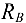 должна быть перпендикулярна балке
должна быть перпендикулярна балке 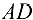 .
.
Сила тяжести вместе с реактивными силами представляет уравновешенную систему сил, произвольно расположенных в плоскости, для которой можно составить три независимых уравнения равновесия.
Составим два уравнения проекций и одно уравнение моментов. Поместим начало осей координат в точке 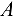 и для упрощения уравнений направим оси
и для упрощения уравнений направим оси 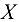 и
и 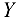 по неизвестным составляющим
по неизвестным составляющим 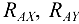 силы реакции.
силы реакции.
Спроецируем все силы на ось 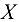 и получим первое уравнение равновесия:
и получим первое уравнение равновесия:
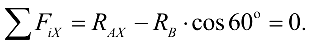
Сила тяжести 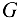 и составляющая
и составляющая 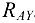 в уравнение не вошли, так как они перпендикулярны оси
в уравнение не вошли, так как они перпендикулярны оси 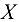 и их проекции равны нулю. Проекция силы
и их проекции равны нулю. Проекция силы 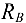 взята со знаком «минус», так как соответствующий ей отрезок
взята со знаком «минус», так как соответствующий ей отрезок 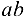 оси
оси 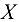 направлен в сторону, противоположную положительному направлению оси
направлен в сторону, противоположную положительному направлению оси 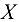 .
.
Спроецируем все силы па ось 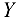 :
:
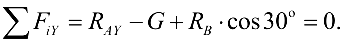
Сила 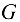 полностью проецируется па ось
полностью проецируется па ось 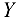 , так как она ей параллельна.
, так как она ей параллельна. 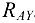 проецируется полностью по той же причине. Проекция силы
проецируется полностью по той же причине. Проекция силы 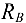 взята со знаком «плюс», так как она совпадает с положительным направлением оси
взята со знаком «плюс», так как она совпадает с положительным направлением оси 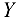 .
.
Для составления уравнения моментов в качестве центра моментов может быть выбрана любая точка плоскости, но для получения более простого уравнения следует воспользоваться следующей рекомендацией: в качестве центра моментов надо выбирать ту точку, через которую проходит большее число неизвестных сил. В таком случае уравнения неизвестных сил в уравнение моментов не войдут, так как их моменты окажутся равными нулю. Из рисунка видно, что в качестве центра моментов следует взять точку 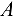 . Тогда третье уравнение будет иметь вид
. Тогда третье уравнение будет иметь вид
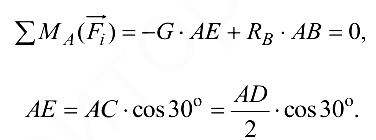
Перепишем уравнение моментов:
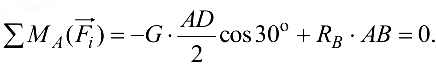
Момент силы тяжести взят с отрицательным знаком в силу того, что он направлен по часовой стрелке. Момент реакции 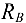 направлен против часовой стрелки, поэтому он взят со знаком «плюс».
направлен против часовой стрелки, поэтому он взят со знаком «плюс».
Из уравнения(3.4)
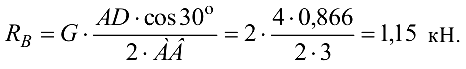
Из уравнения (3.3) получим
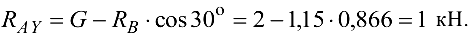
Из уравнения (3.2) найдем
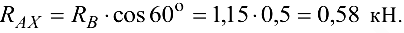
Для проверки правильности решения воспользуемся уравнением моментов относительно точки 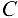 :
:
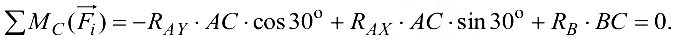
Если после подстановки значений 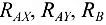 уравнение превратится в тождество вида 0 = 0, то, значит, задача решена верно. Подставив числовые значения, получим — 1 • 2- 0,866 + 0,58 • 2 -0,5 +1,15 • 1 = 0 , т. е. 0 — 0. Задача решена правильно.
уравнение превратится в тождество вида 0 = 0, то, значит, задача решена верно. Подставив числовые значения, получим — 1 • 2- 0,866 + 0,58 • 2 -0,5 +1,15 • 1 = 0 , т. е. 0 — 0. Задача решена правильно.
Полная реакция опоры 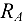 :
:
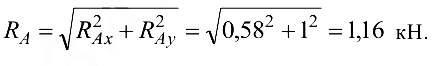
Ответ:
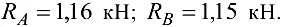
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

