Оглавление:




Одномерное установившееся течение газа вдоль трубы переменного сечения
- Одномерный стационарный газовый поток вдоль трубы с переменным сечением основан на предположении, что параметры газового потока, такие как скорость потока, давление, плотность и т. Д., Являются одинаковыми во всех точках в каждом сечении, перпендикулярном оси трубы. Немного ближе к реальности. Это предположение хорошо соответствует реальности элементарных токовых трубок, но также используется для труб конечных размеров, в которых используется среднее значение сечения трубы.
Сначала мы получим следствия формы уравнения Бернулли из частного случая стационарного невращающегося движения из газового уравнения движения (45). По этой причине левая часть этих трех уравнений (45) выражена в формате Лам Громеча. Игнорируя силу тела, NN о Предполагая, что движение является стационарным А без вихря (OX = O (, = f) z = 0) мы получим из этих уравнений: Умножьте эти уравнения на dx первый, второй dy и третий dz, чтобы получить или. Это уравнение Бернулли в дифференциальной форме. = 1>.
Следует различать чистое качение, когда точка соприкосновения А катка не скользит по неподвижной плоскости, и качение со скольжением, когда наряду с вращением катка есть и скольжение, т. Людмила Фирмаль
Интегрирование (58) из состояния газа, где 0, p = p0; p = p0, каждый с параметром v. p; p, то получается интегральное уравнение Бернулли. (59) Интеграл уравнения (59) зависит от характеристического уравнения. Тип зависимости и уравнение Бернулли Это вызывает баротропный процесс. То есть несжимаемая жидкость p = const принимает вид: или Уравнение Бернулли для несжимаемой жидкости широко используется при рассмотрении многих технических вопросов, связанных с движением жидкости. В этом случае оно обычно обобщается с учетом потенциальных объемных сил, особенно действия силы тяжести жидкости.
Для газа уравнение Бернулли (59) имеет вид p p0 = (p p0) n Переведите уравнение Бернулли в дифференциальную форму газа, чтобы можно было ввести число M. udv + ^^ O; pda + 2 = 0, дп р р Потому что дп дп = а2. Если вы разделите обе части на a2, или Другим уравнением, необходимым для анализа потока газа в трубе с переменным сечением, является уравнение неразрывности или сохранения массы. Получите проблему непосредственно в наиболее удобном формате (рис. 179). Для одномерного потока газовая масса проходит через каждый участок трубы за 1 секунду. м = свп. Где S поперечное сечение трубы. v поток газа; p плотность газа.
- При устойчивом движении одна и та же масса газа должна проходить через все поперечные сечения. То есть m = Svp = const. Давайте логарифмируем это уравнение сохранения массы. получить In u = In S + In g + In p = const Рассмотрим переменную величину S. И; p, возьмите полную разницу с обеих сторон. У нас есть + = 0,1601 Это уравнение неразрывности, необходимое для стабильного одномерного потока идеального газа в трубах различного сечения. Исключите величину dp p из уравнения неразрывности (60) и уравнения Бернулли (58 ). получить S.t (M i). молодежи.
Это уравнение (61) называется уравнением Гюгонио. Используйте уравнение Гюгонио для анализа характера потока газа в трубе с переменным сечением. Из уравнения (61): При M <1, соответствующем дозвуковому течению, знаки величин dS и du меняются местами. Для сверхзвукового потока M> 1 и dS и de имеют одинаковый знак. Другими словами, сверхзвуковой поток распространяется в направлении, противоположном дозвуковому потоку. Чтобы увеличить скорость, нужно расширить трубу. Если M = 1, dS = 0. То есть в этом случае S достигает максимума или минимума.
Вектор углового ускорения е при ускоренном вращении фигуры совпадает с направлением вектора угловой скорости го, а при замедленном вращении эти векторы имеют противоположные направления. Людмила Фирмаль
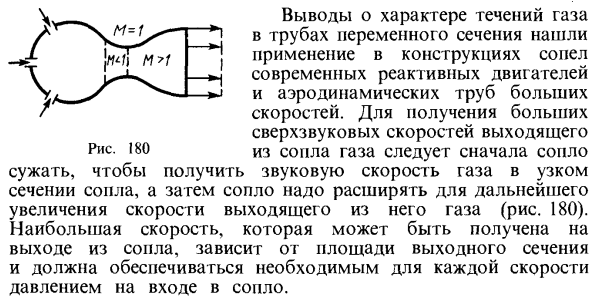
Можно использовать, чтобы показать, что M = 1 может существовать только в самом узком участке трубы (S = Smin). Выводы, касающиеся характера газового потока в трубе переменного сечения, были применены к конструкции современных реактивных двигателей и сопел высокоскоростной аэродинамической трубы. Увеличить сверхзвуковую скорость Направляющая форсунка от RNS газовая.
Узкая часть сопла должна быть сужена для получения скорости звука в газе, а затем сопло должно быть расширено для дальнейшего увеличения скорости газа из него (рис. 180). Максимальная скорость, которая может быть получена на выходе из сопла, зависит от площади выходного сечения и должна обеспечивать давление, необходимое для каждой скорости на входе в сопло.
Смотрите также:
Задачи по теоретической механике
| Установившееся движение вязкой несжимаемой жидкости в круглой цилиндрической трубе | Новая форма основных аксиом |
| Распространение малых возмущений в идеальном газе. Скорость звука | Системы отсчета |

