Оглавление:




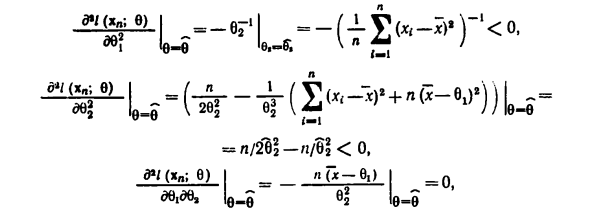

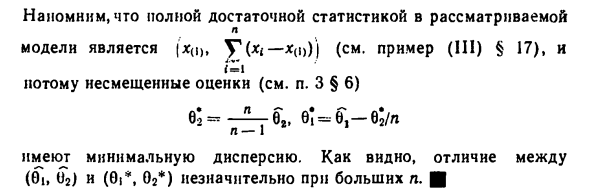



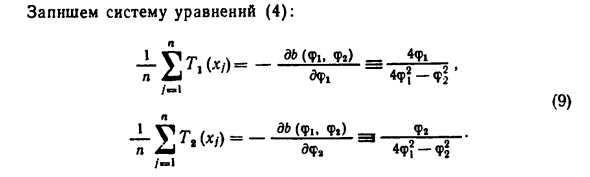

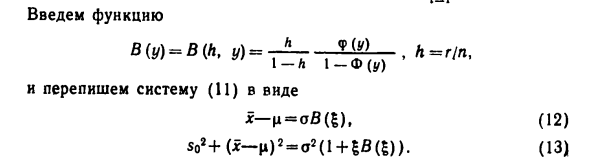



Оценки максимального правдоподобия
- Задг .-. И точечная оценка, решаемая с принципиальной точки зрения Достаточно Достаточно минимальная статистика. Но это остается Какой открытый вопрос достаточно? Статистика должна быть выбрана для оценки конкретного параметрического Функция <р <6). Объективный подход, основанный на выборе Минимальная дисперсия ki подробно обсуждалась в §17. Однако этот подход эффективен Практически маленькая достаточно маленькая размерная статистика Сводится к экспоненциальной модели. Требования Беспристрастность также ограничивает возможность применения метода.
Кроме того, ничто не мешает существованию 5 баллов (X). Небольшое смещение и стандартное отклонение Меньше, чем дисперсия самой высокой непредвзятой оценки. реальность Реализация принципа правдоподобия в задаче точечной оценки Вы можете принять во внимание максимальную оценку истинности Оценка вероятности: 6 (х) оценка, которая максимизирует функцию вероятности L (x; 6 (x))> L (x; c) Или, что эквивалентно, называется функцией логарифмического правдоподобия Вызывается оценка максимального правдоподобия параметра (м.м.с.) Параметр с.
Если статистическая модель является дискретной, (х) 199 Значение параметра 9, при котором наблюдается вероятность Pb (x) Людмила Фирмаль
Образец х Макс наблюдается. В модели непрерывной плотности / (X, 0) значение наблюдения образца x становится максимальным Максимум при 0 = 6 (х). φ @) = (φ | (c), …, (i-c) — * = Производная d / (x „; 0) / d0 меняет знак с минус на плюс, когда: L Проходная точка 6 (xn) = -S (xn) ~ — ] x (= x, поэтому x О программе. м. (II) Повторная выборка из нормального распределения N (μ, a2), положив Gi = u »02 = o2, получим / (Chl; c) = -g дцх „; дл (xn; Q) / d% = -n / 262 + (Jte-xJ + n (x-QJ ) / B • |). я-л Приравнивая производную к нулю, получим (За исключением случая х, } я <в = x, t = 1, …, n) DV? & H ( p, c) е = е (-1 о (Xn; e) в е; б = б
Тогда суди (Dk1db ) (dqdb ) — tcd ^ db ^)> 0 Таким образом, для 8i, 82 функция правдоподобия Максимальное значение (Iii) Для повторной выборки из равномерного распределения @, C) — { Я В противном случае 0. Функция L (xn; 0) равна 8 и равна @@; x (n)], что составляет b точек 8 =. ? (L) После скачка величины xw ~ n она монотонно уменьшается. фронт Формально о. mp не существует, но переопределен Исходная плотность распределения модели, настройка f (x; 0) = B ~ ‘ Если 0 > ei <+ oo. еа> о, Мы получаем f (xn; in, Q2) = -n \ nQ, Очевидно, что максимум 8r / (xn; 0 ,, 02) в 0 | достигнут в 0t-min.v, -X (i). Isugisugun Тогда из уравнения o = -a / (xn; o „e2) / ao2-n / e2-i-y (x (-l) b72 узнать
- Запомните достаточно полную статистику, принятую во внимание L Модель (x (i) (y1 ^ -x (i)))) (см. Пример (III) §17) Следовательно, справедливая оценка (см. §3§6) 02 г Ой н-1 нм ^ Минимальная дисперсия. Как видите, @b 02) и @ | *, 02 *) просто ¦ для крупных предметов 202 Рассмотрим повторную выборку из семейства экспоненциальных функций Экспоненциальный тип с плотностью f (x; b) = A (x) exp (? b, T, (x) +6 (b)), b = @, Qh). , • = 1 Функция логарифмического правдоподобия выборки I (x „: 0) =? A (l-) +? 0? R, (l,) 4nb @). Дифференцирование по 0 „t = l, … K приводит к системе. 0 «d / (xL; c) / dv, =? R, (x,) + ndb (c) / dv, * = 1 фут D) / -i Единственное условие разрешимости системы D)
Невырожденная матрица с). Так что решение системы D) является максимумом функции Вероятность, как известно, положительно определенная Матрица определенности \ -dH {xn; c) / &, = Mv- & 55; — * ‘* / -1 * Это потому, что матрица F) не зависит от chl (см. (E)). F) является матрицей Фишера fx (8) и поэтому будет неотрицательной Неотрицательное определение. Следовательно, при невырожденном условии матрицы, О [d2b (Q) / dQidQj, i, j = \, …, k]. только мп Система D) решение. Со статистикой S (xn) — (S, (xn) Sk (x, J), St (xl) = -Γ, (x /), G) N Если достаточно, статистика 6 (chl), эквивалентная S (xn), Достаточно Помните, что неравенство Фреше-Рао-Крамера перевернуто Равенство оценок G).
Также из отношений ,,; G) — = 0 203 И D) последствия (см. Также результат 1 теоремы 2 в § 19) D) 6 = 6 (х „) Вот так 0 ,, сик. Людмила Фирмаль
Поэтому о. параметрическая функция mp gradefe (G) gradgfeF) объективен и его ковариационная матрица Возьмите наименьшее возможное значение: (Nix (c)) = [-n & bt, i, j = 1, …, n] ~ K Из теоремы 2 § 19 (см. Результаты) и выше Вывод сопровождается следующим утверждением: С условиями регулярности и непредвзятых оценок, Фреше — Рао — преобразовать неравенство Крамера в равенство, тогда Счет около. м. (V) (Xi, Yi), / = 1, …. n два повторных образца LEC 2D нормальное распределение, Q) (см. Пример в пункте 1) §12): / o> a’r \ V A2P A2 / / Введение в параметризацию <Р-!
0. Логарифмическая функция Вероятность X (i) ^ … ^ x, n ‘) имеет вид (см. Пример (VI) §! B) f (x; q, o) = c + r 1nA-Φ ((xm-q) / a)) — nina- Где f (x) -f.r. Нормальный закон N @, 1), φ (x) = Ф ′ (dc). Put N N Написать систему уравнений правдоподобия (Р) да Ввести функции VMVLY. «GL Перепишите систему A1) в следующем формате A2) A3) 205 Подстановка уравнения А2) в А3) дает: 502 + a2H (| J = o2A + | H (|)). A4) С другой стороны, используя уравнение А2), a | = X (, V) — == X (A ‘-> x + (x-X) = X (.V) -x + afl (s), Откуда o = (x (.V) -x) / (s-B (|)). A5) Если вы замените А5) на А4), ура увеличится
Discovery for Discovery |: Уравнение А6) решается численно. Заменить его решение на f В A5), найдите, и вместо этого получите в | и A2) с, и более удобная формула использования. перераспределение Установите, используя член A5) в уравнении A4) 4E) = fl (S) / (flF) — &). A7) Мы получаем Подстановка A5) в A2) дает Поэтому о. м. Представлено формулой U = * + X (?) (* <«> -X), a2-s02 + A. (F) (x (A) -fJ, A8) Где 5 определяется из уравнения А6). Иметь практическую возможность насладиться оценкой » А8), достаточно рассчитать для разных h = r / n в таблице
Решение уравнения А6): (! -Fl (L.lJ-lB (h, t)) l (l-B (h, 6)) — v A9) Значение у получено в несколько шагов. Альтернатива решения Получите таблицу значений g = s (A, y), H, = l (A, y) в уравнении A7). Такой таблицей, рассчитанной Коэном, является [9, с. 147- 148]. Проиллюстрируйте описанную методологию примерами из (I) §11. Где l = 10; g = 3; N = 7; d = 0,3; x = 1,70471; so2 = O, OO3514; * (L-) = 1,778. Тогда v = so2 / (* w — xJ = 0,654. Из таблицы [9, с. 148], интерполяция для y находит A = 0,512. подмена Заменено А8), (G = 1,742; а = 0,079. Подробное объяснение этого примера приведено на с. 150- 151 [9].
Смотрите также:
| Границы дисперсии при нарушении условий регулярности | Метод Монте-Карло в модели сдвига-масштаба |
| Функция правдоподобия | Проверка статистических гипотез |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.

