Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и производные функции различных порядков.
Символически дифференциальное уравнение можно записать в виде
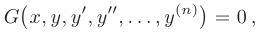
где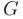 
— некоторая функция 
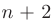переменных 
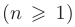. При этом порядок 
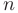старшей производной 
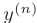, входящей в уравнение, называется порядком дифференциального уравнения.
Решением дифференциального уравнения называется такая функция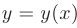 
, которая при подстановке ее в это уравнение обращает его в тождество. Например, функция 
является решением уравнения 
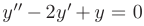, так как 
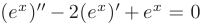при любых значениях 
.
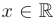График решения дифференциального уравнения называется интегральной кривой.
Пример:
Найти решение уравнения 
. ► Проинтегрируем данное уравнение 2 раза:
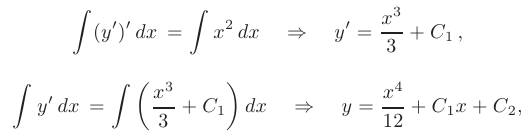
где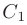 
и 
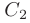— произвольные постоянные. То есть решение получено принципиально неоднозначное. Следовательно, дифференциальное уравнение задает не одну, а целое семейство интегральных кривых на плоскости.
Для выделения из семейства определенной кривой (решения) в данном случае достаточно задать точку, через которую проходит искомая интегральная кривая и направление, в котором она проходит через эту точку, т.е. задать значения:
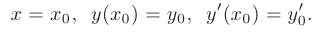
Например, если задать
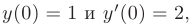
то получим:
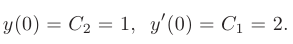
Подставив значения констант 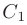и 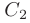, приходим к решению:
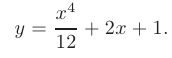
Для выделения однозначно определенного решения дифференциального уравнения 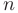— го порядка следует задать дополнительно 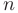условий. Условия такого рода обычно называют начальными.
Общим решением дифференциального уравнения 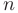-го порядка называется такое его решение 
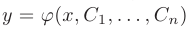, которое является функцией переменной 
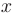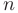и произвольных независимых постоянных 
.
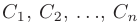Частным решением дифференциального уравнения называется функция, полученная из общего решения подстановкой конкретных числовых значений произвольных постоянных .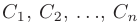
В примере 7.1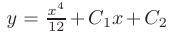 
— общее решение, 
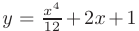частное решение дифференциального уравнения 
. Дифференциальное уравнение называется разрешенным относительно старшей производной, если оно имеет вид:
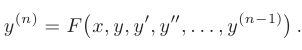
Например, уравнение
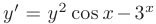
разрешено относительно первой производной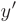 
искомой функции 
.
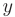К дифференциальным уравнениям приводит ряд задач экономики, механики, биологии, социологии и т. д.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
