Оглавление:








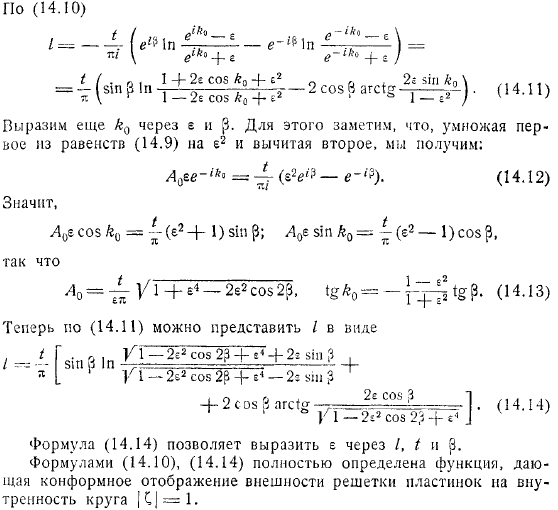




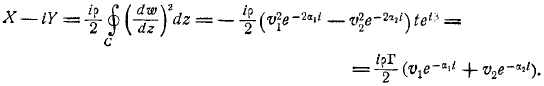

Обтекание решетки
В качестве первого обобщения задачи о движении профиля в гидромеханике рассмотрим систему, состоящую из решетки, то есть бесконечного профиля, который может быть образован путем перемещения профиля на одинаковое расстояние. Это расстояние называется шагом сетки. Решетки имеют важные применения в теории турбин. Задача о решетках сводится к задаче о перемещении крыла в трубе, задаче о воздействии на воду в канале, окруженном параллельными стенками, и др. В будущем ее можно будет развивать и дальше.
Ось вдоль хорды профиля решетки. Ось и угол, образованный, являются направлениями, в которых профиль решетки должен быть сдвинут на шаг для получения смежного. Называется удаление решетки. Значение — это период решетки. Рассмотрим потенциальный поток вокруг решетки со скоростью угол слева от решетки под углом, который является относительно. Дальняя задняя часть штанги справа, в общем случае, под углом по отношению к оси. Еще одна рампа с наклоном, имеет Жуковского.
Естественно предположить, что поток, обтекающий решетку, является периодическим и является периодом. Возле каждого профиля различают линии потока, на обоих концах которых бесконечно простираются влево и вправо, между которыми расположены профили, полученные друг от друга посредством смещения на ступень решетки. Эти строки совпадают. Ввести вспомогательную плоскость и выполнить внешнее конформное преобразование профильной решетки к многовалентной римановой поверхности плоскости в системе концентрических окружностей радиуса. Вы получаете многозначное соответствие между.
Каждая точка в единичном круге плоскости соответствует множеству совпадающих точек в плоскости. переместите точку в точку (действительное число, положительное значение, меньше) и точку. Движется к. Если мы повернем точку по окружности с малым радиусом, то достигнем той же точки в плоскости. Напротив, в плоскости мы достигнем ближайшей конгруэнтной точки. То же самое можно сказать и о окружности точки.Таким образом, отображение совпадающих кривых и каждой полосы между и внутренним контуром окружности в разрезе между точками: в этом случае контур профиля вводится в круговой контур, а кривая конгруэнтности вводится в разрез (также известный как) между.
- Изометрическое отображение. Пусть кроме того, при решении задачи можно вывести. Форма функции может быть определена сразу по. Другими словами, можно рассматривать как комплексный потенциал воображаемого потока внутри единичного круга плоскости. Жидкость течет из точки и течет в точку. Кроме того, приведите новое значение, обойдя небольшой круг вблизи точки. В точке имеется вихрь и источник, а в точке вихрь и сток. Эго означает, что имеет простой полюс в точке, где есть. Тогда над окружностью имеет точки; аргументы соответствуют критической точке профиля плоскости.
Расположение этих точек заранее неизвестно, но мы знаем, что должны исчезнуть в этих точках. Наконец, поскольку на диске, вы можете расширить на всю плоскость комплексной переменной, поместив более простых полюса в точке (инвертированное преобразование) при. Регулярность приводит к тому, что в случае будет нулем. При этом сразу где комплексное число. Параметры определяются геометрическими свойствами профиля и условиями течения.
Обратите внимание, что просто связан с циркуляцией вдоль контура каждого профиля. Дело в том, что циркуляция вдоль контура профиля плоскости берется против часовой стрелки и равна циркуляции окружности, берется стрелка по часовой стрелке, последняя определяется через сумму остатков полюсов, поэтому m пишут: таким образом, циркулирующая должна быть реальной, поэтому сумма считается реальной. Вместо введем новое, но уже из уравнения к действительному числу равно, где допустимо.
Обратная решётка — точечная трёхмерная решётка в абстрактном обратном пространстве, где расстояния имеют размерность обратной длины. Людмила Фирмаль
Далее, мы покажем, как решить проблему, используя поток вокруг сетки плоской пластины в качестве примера. Во-первых, функция — возьмем формулу и дадим конформное отображение плоскости с выемкой внутри окружности. To получаем функцию, используем гидродинамический метод. Это самое простое сравнение потока одной плоскости и. Другими словами, рассмотрим новый простейший поток в плоскости со скоростью, параллельной профилю, то есть без потока циркуляции вокруг сетки. Скорость этого потока равна. Комплексный потенциал этого простейшего потока равен.
- Какой поток соответствует этому некруглому потоку плоскости. Чтобы ответить на этот вопрос, используйте формулу, чтобы сначала выбрать параметр и получить гамму. Согласно, это означает в этом случае теперь обозначается. Поэтому, где действительные числа. При интегрировании и рассмотрении получается следующее. Удобно ввести уравнение вместо параметров новых параметра из, дающие конформное отображение, принимают вид. Легко видеть, что становится циклом сетки плоскости.
Поэтому после патрулирования вместо количества с учетом периода и ширины каждой пластины определяется сетка плоскости. Теперь соединяем параметр с шириной пластин, составляющих решетку, параметр. Соответствует значению передняя кромка является точкой, следовательно, ширина пластины равна ширине уравнения должна определяться, потому что подоконника также крыло и выражается следующим образом: заметим, что для этого, умножив первое равенство на и вычитая, получаем потому что, следовательно.
Ну, согласно, потому что, указав грехов не потому что; уравнение позволяет представлять, т и п. Формула полностью определяет функцию, которая сопоставляет внешнюю сторону решетчатой пластинки к внутренней стороне окружности. Теперь мы возвращаемся к проблеме потока. Комплексный потенциал удовлетворяет уравнению. Если мы интегрируем это уравнение в, мы получим в функции. С другой стороны, дают соответствие между.
Поэтому остается только выбрать параметры, которые будут включены в. Параметр характеризует геометрический аспект потока. Она уже определена в. Для нахождения параметров используем условия величины и направления скорости на бесконечности перед пластиной и конечности скорости на задней кромке пластины. Чтобы определить скорость плоскости, используйте экватор и получите конечную скорость на заднем конце размер, который является осью (направление пластины) и углом.
Тогда, если, это будет, поэтому потому что отсюда, отому что, потому что из этих уравнений можно найти, что полностью определены. Также найдите циркуляцию. Используя равенство, замените на. Есть случаи обтекания одной пластины, которая переходит в предел, например приведет к для малого, тогда и приведет к равенству, что совпадает с формулой этой главы. И использовать для получения. Заметим, что зависимость также получается в случае любых контуров профиля, обтекаемых с циркуляцией.
Факт, вспомним отношение, в котором интегрирование осуществляется по контуру профиля. Выделим область. Ограниченную схему и схему, смежных конгруэнтных линий тока, состоящих из сегментов, и прямых сегмента, параллельных периоду решетки. В пределах выбора функция является. Интеграл, взятый против часовой стрелки вдоль контурной линии равен минусу от интеграла контура, взятого по часовой стрелке.
Однако интегралы отрезков, взятые в противоположном направлении, исчезают из-за периодичности функции, где мы удаляем отрезки бесконечно и оставляем их параллельными себе. Наконец, это выглядит так. Поэтому справедливо в любом случае, а не только в случае прямого контура. Можно легко найти, если вы используете новый путь из общей формулы Чаплыгина, мы используем.
Понятие обратной решётки удобно для описания дифракции рентгеновских лучей, нейтронов и электронов на кристалле. Людмила Фирмаль

