Оглавление:

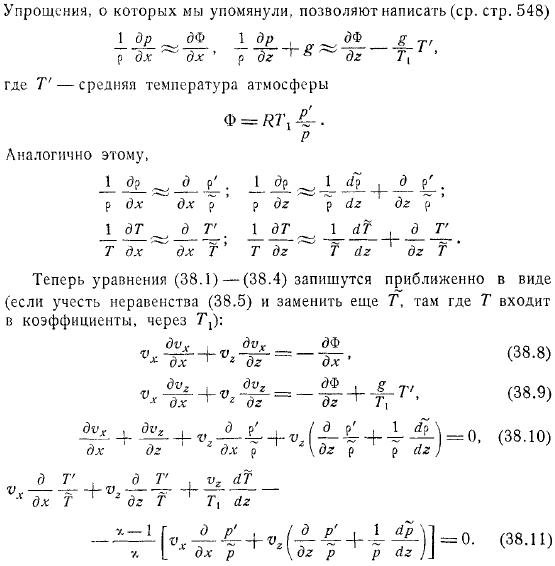




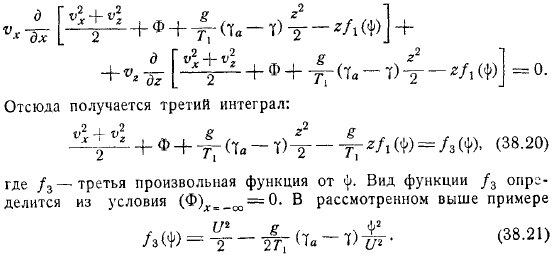



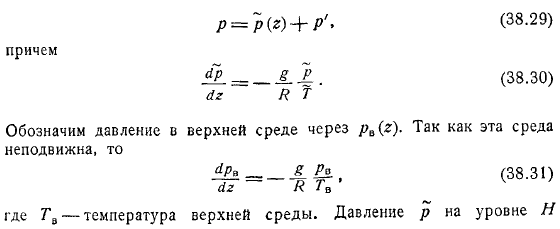

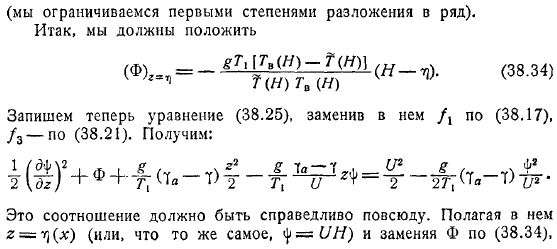



\

Обтекание препятствия тяжелой сжимаемой жидкостью. Длинные волны. Бора
Давайте вернемся к вопросам потока, которые мы рассмотрели. На этот раз мы не будем линеаризовывать уравнение, а упростим его, как в теории конвекции. Начальное выражение является.
Давайте упростим конвекцию, как и в предыдущей статье. Я предполагаю. Положительное «стандартное» значение является, соответственно, известной функцией высоты возмущения, вызванного.
- В то же время с упрощениями, которые мы только что упомянули, средняя температура атмосферы. Это вот так.
- Теперь уравнение можно записать примерно в следующем виде (если учесть неравенства и заменить места, входящие в коэффициенты).
По стандарту. Так что моя температура меняется на высоте. Людмила Фирмаль
Очень точно, мы можем предположить гидромеханику, что уравнение неразрывности пренебрежимо мало по сравнению с остальными, и мы можем записать его в виде.
В атмосферных условиях член этого уравнения является первыми незначительными частями. Наконец, мы обсуждаем уравнения непрерывности вида. Аналогичное упрощение применяется к уравнению теплового потока (например, игнорируя содержащиеся в нем термины).
- Не место, которое можно считать постоянным, а окончательное принятие. Задача будет состоять в том, чтобы определить функции из уравнения.
- Эти уравнения имеют интеграла. Помогает разрушению плотины ввести функции потока из уравнения.
Теперь уравнение можно записать в виде. Или (для констант). И получить первый интеграл. Является произвольной функцией. Мы исключаем функции не только из производной, но и из формул, которые вычитают друг из друга.
Используйте интеграл и будьте осторожны с ним. Людмила Фирмаль
Эта формула эквивалентна следующей, как вы можете легко видеть. Является новой произвольной функцией. Функция может быть определена из следующих критериев.
Существует поток с постоянной скоростью, и текущая функция связана с отношением. С другой стороны, у нас есть. Это соотношение должно быть справедливым. Далее, следовательно, и поэтому мы должны.
Решите уравнение. Как только он известен, он определяется из того, что ему остается только быть. To находим, умножаем и складываем. Используйте его и получите его без проблем. Это даст вам интеграл .
Здесь произвольная функция типа функции определяется из. Пример выше. Поговорим о граничных условиях задачи. Возьмем уравнение обтекаемого профиля препятствия в виде. Тогда из граничных условий.
Или, по определению, до постоянного срока, и это можно предположить. В качестве граничных условий сверху можно принять наличие горизонтальных стенок. Или именно поэтому в конкретном случае анализа мы получаем бесконечную и постоянную скорость.
Другим типичным условием является условие наличия свободной поверхности в верхней части. Форма этой поверхности определяется вместе с общим решением. To запишите это состояние, вам нужно принять участие.
Теперь перейдем к подробному рассмотрению случая длинных волн. Для длинной волны уравнения отбросьте левую сторону. И это в конечном счете, вместо уравнения, которое мы получаем в настоящее время.
Теперь вместо этого перепишите уравнение без изменения. В качестве конкретного примера рассмотрим проблему борьбы с холодным воздухом, проходящим через гребень). Уравнение сечения гребней.
Предположим, что воздух находится над холодным потоком. Уравнение поверхности, разделяющей теплое и холодное. Тип функции заранее не известен. Возьмем тогда и из уравнения, чтобы удовлетворить отношение, оно записывается в следующем формате.
Вы должны решить это уравнение при граничных условиях. Мы считаем его обыкновенным дифференциальным уравнением (оно входит в параметрическое). Возвращает решение, удовлетворяющее заданным граничным условиям.
Эта формула пока не известна. Используйте граничные условия давления, чтобы найти. При прохождении через поверхность должна быть непрерывность давления. Напомним, что давление движущегося воздуха имеет следующий вид.
Больше показывает формулу Коши — Гельмгольца давление верхней части. Эта среда неподвижна, где температура верхней среды. Вы можете интегрировать и писать основанный на непрерывности давления. Теперь нам нужно равное давление на поверхность.
Теперь, когда вы запустите интеграцию, вы получите следующее. Ограничение на начальную степень расширения в ряду. Поэтому нам нужно поставить. Напишите уравнение здесь и замените его. Вы получите. Это соотношение должно применяться везде.
Положите его (или, эквивалентно). Где вы получаете уравнения, которые могут быть определены из. Здесь вводится безразмерный параметр. И обратите внимание, что по определению, чтобы достичь следующего трансцендентного уравнения.
Для анализа удобно вводить безразмерные величины. В этом случае известные и неизвестные величины связываются уравнениями, содержащими безразмерных (заданных) параметра. Параметры характеризуют «толщину» холодной массы, представляя собой скачок, который температура претерпит при переходе от холодной массы к теплой массе.
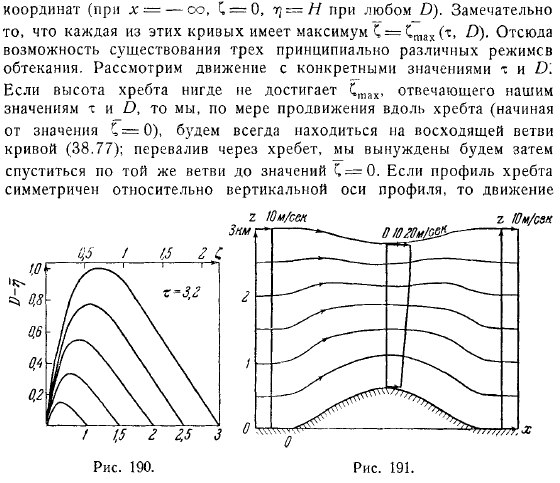
Если сделать поправку, то она может быть выражена в виде изогнутой линии на плоскости. С заданным значением, вы можете получить проблему и решить ее. Отображается семейство кривых с различными значениями.
Здесь отображаются вертикальная ось и горизонтальная ось. Все кривые проходят через первую координирует. Самое замечательное, что каждая из этих кривых имеет максимальное значение. Таким образом, показана возможность существования принципиально разных режимов работы жидкости.
Рассмотрим движения, которые имеют определенное значение. Если высота выпуклости не достигает точки, где она соответствует значению, она всегда будет восходящей ветвью кривой, когда она движется вдоль гребня (начиная со значения). После пересечения хребта, необходимо спуститься к значениям по той же ветке.
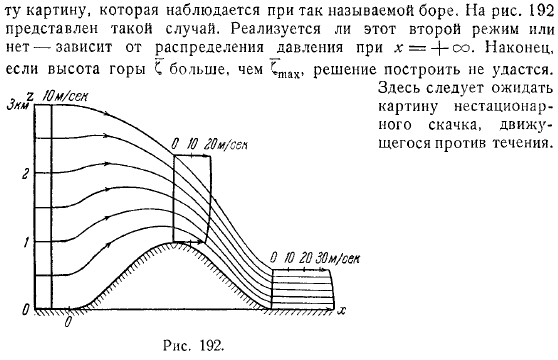
Если приподнятый профиль симметричен относительно вертикальной оси профиля, то движение. Он также будет симметричным. Этот случай представлен выше. Она интерпретируется как.
Делаю так, режим может произойти при том же значении, если максимальная высота обтекаемого гребня точно. В этом случае двигайтесь вдоль хребта и поднимайтесь по кривой, пока не пройдете хребет и не достигнете точки. Вы можете использовать решения.
Из них соответствует возврату в точку вдоль восходящей ветви кривой. Это решение по своему характеру идентично решению, соответствующему первой администрации. Другое решение соответствует спуску по нисходящей ветви кривой.
Здесь нарушается симметрия (даже в случае симметричного профиля): при спуске скорость увеличивается. Фотографии, которые наблюдаются с так называемым бором .Этот случай будет представлен.
Будет ли реализован этот второй режим, зависит от распределения давления. Наконец, если высота горы больше ее, то решение о строительстве терпит неудачу. Чего следует ожидать от нечестивых Зыбкие картинки прыжок, который движется против течения.

