Оглавление:


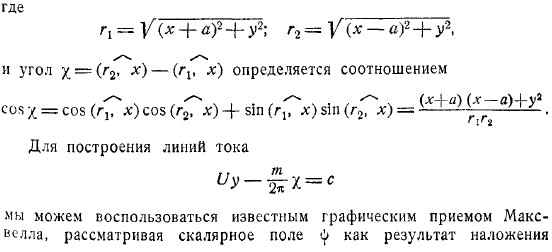









Обтекание некоторых форм профилей цилиндров
Если картина течения при обтекании кругового цилиндра чисто поступательным потоком (без циркуляции) могла быть получена гидромеханикой внесением в поток некоторого дублета, то естественной представляется задача определить, какие формы профилей обтекания могут быть получены той или другой комбинацией источников и стоков. Задача эта является обратной задаче определения комплексного потенциала при обтекании цилиндрического тела заданного профиля. Мы рассмотрим здесь лишь некоторые простейшие комбинации источников и стоков.
- Источник и сток равной обильности т, помещенные на вещественной оси в точках — при наличии однородного поступательного потока, скорость которого в бесконечности плоской пластинки направлена вдоль оси, дают течение с комплексным потенциалом. Потенциал скорости и функция тока выразятся формулами где и угол определяется соотношением. Для построения линий тока мы можем воспользоваться известным графическим приемом Максвелла, рассматривая скалярное иоле как результат наложения друг на друга более простых скалярных полей и линиями уровня которых служат пучок прямых, параллельных оси, и пучок окружностей, проходящих через точки.
Построив эти линии уровня через равноотстоящие значения с линиями второго, параметры которых удовлетворяют условию. Мы получим ряд точек на линии тока. Производя указанное построение, мы можем убедиться, что линия тока состоит из части вещественной оси, внешней по отношению к отрезку. На концах этого отрезка, являющихся критическими точками течения, где скорость обращается в нуль, линия тока разветвляется, образуя профиль овальной формы; ордината, при, соответствует максимальной ширине овала и определяется как корень трансцендентного уравнения.
Таким образом, комплексный потенциал дает картину обтекания цилиндра, ограниченного указанным овальным профилем. Точечный источник обильности и система линейно-распределенных стоков, суммарная обильность которой равна обильности источника, помещенные в поступательном потоке на прямой, параллельной скорости, дают картину обтекания профиля, несимметричного относительно поперечной оси. Взяв упомянутую прямую за ось, поместим начало координат в источнике; пусть координаты начала и конца прямолинейного отрезка, на котором непрерывно распределены стоки, будут.
Тогда комплексный потенциал течения, создаваемого одними стоками, будет. Присоединяя сюда потенциал источника и потенциал однородного потока и отбрасывая несущественное для исследования потока постоянное слагаемое, получаем суммарный потенциал. Выражение для комплексной скорости показывает, что условие удовлетворяется. Течение имеет две критические точки, лежащие на вещественной оси, в которых скорость обращается в нуль; их абсциссы найдутся как вещественные корни трансцендентного уравнения.
В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии. Людмила Фирмаль
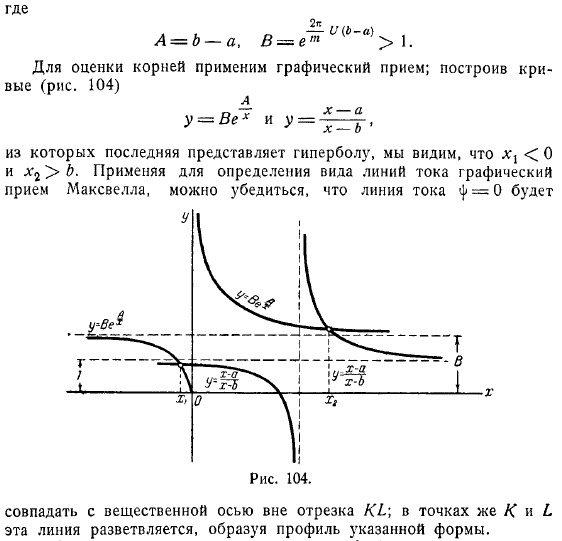
Для оценки корней применим графический прием; построив кривые из которых последняя представляет гиперболу, мы видим, что. Применяя для определения вида линий тока графический прием Максвелла, можно убедиться, что линия тока совпадать с вещественной осью вне отрезка в точках же и эта линия разветвляется, образуя профиль указанной формы. Система бесконечного множества дублетов с одинаковыми моментами, одинаково направленными параллельно вектору и помещенными на прямой, перпендикулярной в расстоянии друг от друга, создает течение с комплексным потенциалом если взять указанное на расположение осей профилей Жуковского.
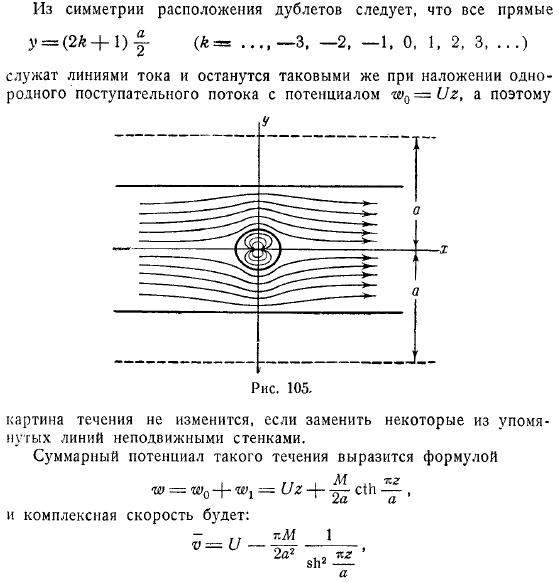
- Вспоминая известное разложение на простейшие дроби. Из симметрии расположения дублетов следует, что все прямые служат линиями тока и останутся таковыми же при наложении однородного поступательного потока с потенциалом, а поэтому картина течения не изменится, если заменить некоторые из упомянутых линий неподвижными стенками. Суммарный потенциал такого течения выразится формулой, и комплексная скорость будет: а откуда видно, что. Критические точки течения определяются условием из которого видно, что течение будет обладать двумя критическими точками, лежащими на вещественной оси на равных расстояниях от начала координат.
Обозначая это расстояние через, мы можем выразить через него величину момента дублетов и тогда отсюда найдется функция тока. Это выражение показывает, что линия тока будет состоять из части вещественной оси, внешней по отношению к отрезку, соединяющему критические точки, в которых линия тока разветвляется, образуя овальный профиль; максимальную ширину этот овал будет иметь при, так как тогда ордината соответствующая максимальной ширине, найдется как наименьший положительный корень трансцендентного уравнения.
Если мало по сравнению с, то будет близко и упомянутый овал будет мало отличаться от окружности. В самом деле, полагая, перепишем предыдущее уравнение в виде. Разлагая обе части в ряды по степеням, будем иметь: откуда видно, что если мало, то будет близко. Таким образом, комплексный потенциал дает картину обтекания профиля, близкого к круговому, помещенного в прямолинейный канал с твердыми стенками, если линейные размеры овала малы по сравнению с шириной канала.
Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический. Людмила Фирмаль

