Оглавление:



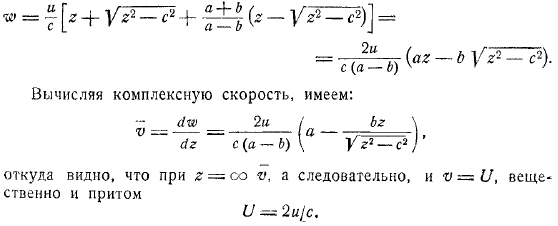
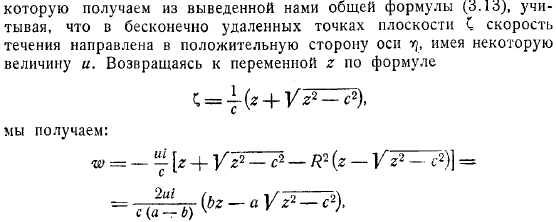

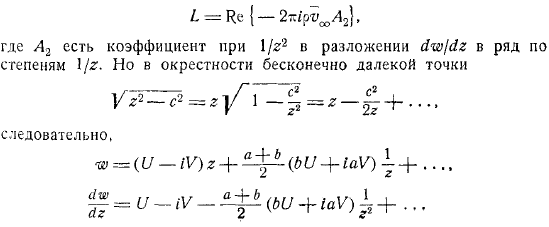


Обтекание эллиптического цилиндра
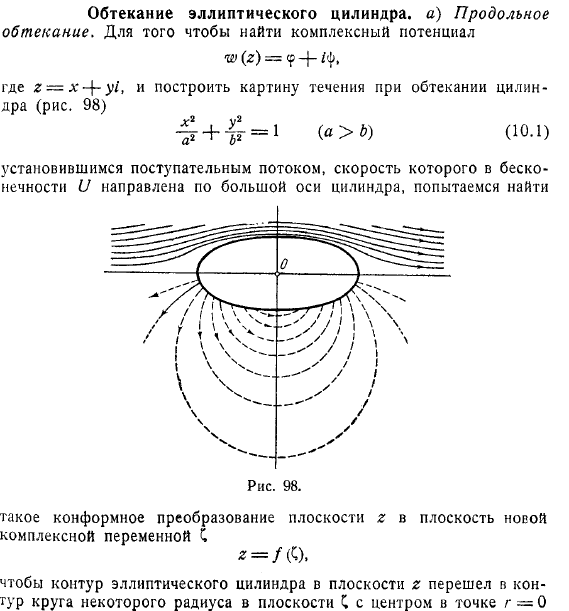
Найти комплексный потенциал и построить схему течения гидромеханики в обтекаемом цилиндре попробуем найти конформное преобразование новой комплексной переменной в плоскости в плоскость новой комплексной переменной так, чтобы контур эллипсоида в плоскости проходил через окружность радиуса с плоскостью, обусловленной устойчивым поступательным потоком, в котором скорость бесконечности направлена вдоль главной оси цилиндра.
Внешняя часть плоскости для цилиндра соответствует внешней части плоскости для цилиндра. Используя известную формулу, мы строим потенциал комплексного потока, когда он обтекает цилиндр в плоскости, совершаем обратный переход и получаем искомый потенциал потока в плоскости. Для этого сначала преобразуйте подобие заранее. Где линейный эксцентриситет этого эллипса.
Тогда эллипс соответствует плоскости эллипсоида, где, а его линейный эксцентриситет равен. Точки соответствуют точкам. Из теории конформных преобразований известно, что перестановка преобразует эллипсоид на плоскости эксцентриситета в окружность на плоскости радиуса с центром в точке; кроме того, если, то внешняя часть эллипса входит во внешнюю часть окружности и выбирает радиус для идентификации эллипсов эти уравнения не являются независимыми и могут быть ограничены. Если вы добавите его, таким образом, желаемое преобразование будет.
Принимая известное уравнение комплексного потенциала потока плоскости, когда скорость течет вокруг кругового цилиндра параллельно действительной оси на бесконечности: в дополнение к скорости и co должны быть выбраны, чтобы быть получены в плоскости при, параллельность потока между плоскостью и плоскостью неявно подтверждается. Обратное преобразование преобразования неоднозначно при, но становится парабола устойчивости более ясным по требованию. Фактически, о точке, это выглядит так: эта точка должна быть на круге радиуса. То нужно получить верхний знак.
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Людмила Фирмаль
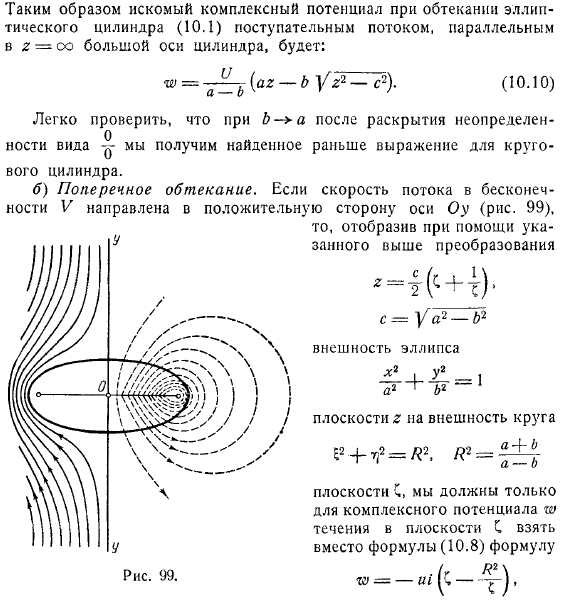
- Значение этого корня, которое положительно для. В результате комплексный потенциал преобразуется в вычислительную форму комплексной скорости, и, следовательно, существенно равна длине эллиптического прогресиба параллелизма цилиндра, следующим образом: можно использовать. Когда, легко видеть, что формула окружности получается после того, как обнаруживается неопределенность формы цилиндра. Бокового потока: если скорость потока бесконечности направлена в положительную сторону от оси, используя вышеупомянутое преобразование плоскости, вместо потока используется комплексная формула формула, вне эллипса плоскость.
Вне окружности обтекаемой плоской пластинки , в точке бесконечности в плоскости, скорость потока направлена в положительную сторону оси, которая имеет определенный объем и получается из выведенной общей формулы. Формула. Возврат к переменной, если существует комплексная скорость потока в плоскости, чтобы иметь, поэтому я получаю следующее: следовательно, искомая формула для комплексного потенциала: косой поток.
Если скорость бесконечности равна вертикальной оси эллипса и некоторому углу, разложить вектор на составляющие, учитывая косой поток как дополнительный результат продольного и поперечного обтекания точек на бесконечности. То комплексный потенциал такого результирующего потока вычисляется как сумма величин: линейности уравнения Лаплас, удовлетворяющий. Поскольку циркуляция отсутствует, сила, действующая на цилиндр в смешанном потоке, уменьшается до сет, а ее момент можно получить, применив формулу, где коэффициент расширения в ряду степеней.
Но поскольку вблизи бесконечной точки и следовательно. Таким образом, замените формулой и, наконец, получите о моменте вращающейся пары: последнее уравнение показывает, что реакционный момент течет в продольном направлении и в поперечном направлении вокруг эллиптического цилиндра.
Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей). Людмила Фирмаль

