Оглавление:




Общий процесс приведения
Общий процесс приведения. Как и процесс накопления (4.1), обсуждаемый здесь процесс (3.7) является не только наиболее общим, но и стандартным.
- Другими словами, он характеризует стоимость одной денежной единицы во времени.
Выразите некоторые аспекты этого процесса и лучше поймите это на примерах. Людмила Фирмаль
Во-первых, легко подтвердить, что PN (4.1) действительно отвечает на вопрос: через некоторое время t> 0, какое количество u (t) поворачивает одну валютную единицу на счете в момент O ?
Однако инвесторов чаще интересует другой «симметричный» вопрос: какую общую сумму v (t) в настоящее время необходимо учитывать? В момент времени 0 после определенного времени t> 0 это одна валютная единица?
- Конечно, при условии, что ITP 6 (t) все еще действителен для учетной записи. С представленной выше концепцией CR, на подобные вопросы можно ответить быстро и в более общих случаях. То есть CD A ( 0.
Таким образом, v (t) является одной денежной единицей после счета, время t. Во-вторых, ясно, что
процесс (4.4) фактически представляет левое крыло расширенного PN. Людмила Фирмаль
Точнее, отражение значения этого процесса на плоскости (£, у) для прямой t = 0, т.е. v (t) = t> 0. Фактически, если 8 (t) =, то ^ (~ y) dy = [8 (y) dy = In t> 0. Jo И для нас функция (4.4) является первой рассматриваемой учетной записью t лет назад
Выполните передачу значения суммы от времени t> 0 к времени 0. Он дает значение в денежных единицах в момент времени 1, но естественно назвать его процессом сокращения (PP), поскольку с его помощью можно легко указать стоимость определенной суммы в данный момент времени в момент 0 ,
То, что конкретная денежная стоимость связана с одной фиксированной точкой в будущем, но возвращается к т годам. Ну, это самый распространенный способ перевести такие расходы, так как это делается с учетной записью с любым SIP 6 (т).
Тем не менее, мы можем говорить об этом переводе немного по-другому: значение v (t) означает относительное уменьшение суммы депозита соответствующего счета в момент времени t, подсчитываемый в противоположном направлении, что является наиболее распространенным
Это не только цель, но и самый простой вариант. Действительно, на практике обычно рассматриваются более сложные ситуации, когда необходимо определить стоимость потока платежей. В какой-то момент в прошлом или будущем, некоторые суммы из-за разных моментов времени.
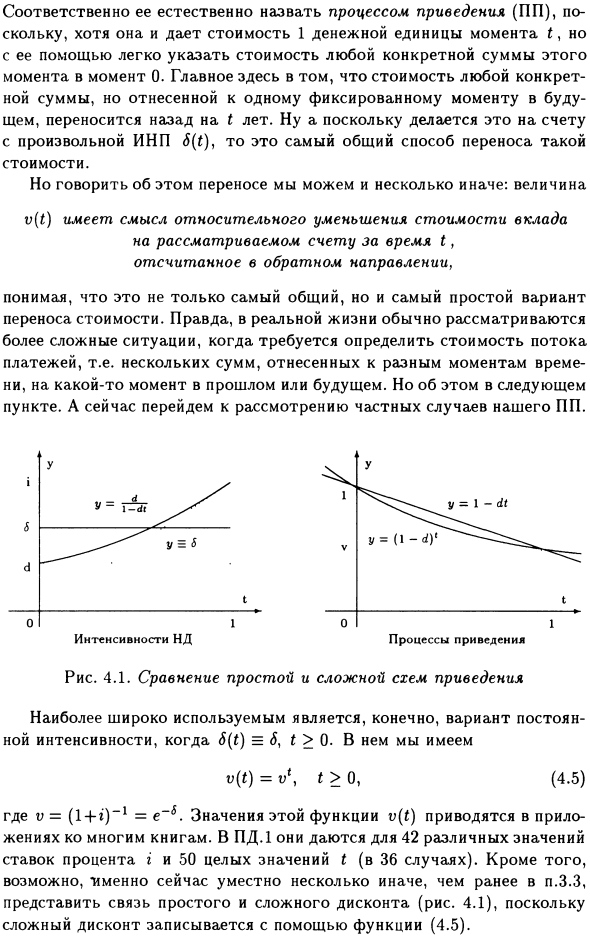
Однако мы подробно остановимся на этом в следующем параграфе. А теперь мы рассмотрим особые случаи нашего программного обеспечения. Рисунок 4.1. Сравнение схем простоя и комплексных сокращений.
Конечно, наиболее широко используются варианты с постоянной силой, где 6 (t) = 5, где t> 0. v (i) = t> 0, (4.5) где v = (1-H) -1 = e ~ &. Значение этой функции v (t) можно найти во многих приложениях к книге.
В PD.1 процентные ставки приведены для 42 различных значений g и для 50 целых значений t (для 36). Кроме того, сложные скидки регистрируются с помощью функции (4.5), поэтому соотношение между простыми и сложными скидками может быть выражено, поскольку оно немного отличается от предыдущего в разделе 3.3 (рисунок 4.1). ,
Однако часто используются другие кусочно-постоянные силы. Пример 4.3. Найти функцию v (t) с силой 6 (t) из замечания 1.3. Решение. Интеграл Jq 6 (y) dy является явно непрерывным и линейным по сечению постоянной интенсивности.
При этом вы можете легко получить exp (-0.09t), exp (-0.05-0.08t), exp (-0.15-0.07 £), v (t) =. О 10 • Хорошо известно, что прочность неоднородна и записывается как 6 (r) = p + rn ^ 7- (4-6). Эта формула называется формулой Стадли.
Легко показать, что вы пишете ПП. ПП — средневзвешенное значение двух ПП постоянной, но разной прочности. Точнее, уравнение v (t) = Y1 (0 + TY) ^ (0- (4.7) 14-1 + r, где vi (t) = exp (- (p + s) t), v2 (t) = exp (-pt)
На самом деле из (4.6) v (t) = exp {-6 (y) dy} = exp {- (rsesy 1 + ge3Y dy} = exp {- (p + s) t + [In (1 + rejy)] o) = формула Стадли часто используется страховыми компаниями для оценки арендной платы, различных контрактов и т. д.
Пример 4.4 Функция v (t) и значение v ( Найти 10), т. Е. PP1, INP в денежных единицах с моментом t = 10 в момент времени 0, заданный уравнением (4-6), где p = 0,07961, r = 0,5, s = 0,121890. : Выражение (4.7), | exp [- (0.076961 + 0.121890) *] + | exp (-0, 076961 *) = • Jо | (1.22) — ‘+ | (1.08) -‘
Предпочтительной денежной единицей P1 является v (10) = ^ (1,22) — ‘° + | (1,08) _1О = 0,24566 * • J сенсорный Не забывайте, как упоминалось выше, что v (t) является ретроспективным уменьшением суммы депозита: Пример 4.5 SIP работает на счете 6 (t) = ae ~ bt, t> 0
Предположим, что один вкладчик вносит 1000 раз в четыре года четыре раза подряд с конца года 1. 1) Найдите функцию v (t). Предполагая, что 6 (0) = 0,1 = 26 (10), 2) определите PP для всех 4 платежей.
Стоимость этого DP в это время 0, и 3) этот DP находит определенный IPI с тем же PP. Решение. 1. Согласно уравнению (4.4), v (f) = exp {- [ae to by dy} = exp -7 (1-e до bt Joo2. 2. a = 0,1, e «10b = 0,5, b = 0,069315, Таким образом, предполагая, что PP для всех платежей равна сумме PP для каждого платежа, мы получаем V = 1000 [и (1) 4- и (2) 4- и (3) 4-v ( 4)] = 3205,43 3.
Вполне естественно определить постоянную IIT 6, полученную из уравнения 1000 [e «5 4th» 26 4th «35 4th» 46] = 3205,43, (4.8) в будущем. Мы уделяем большое внимание не только ПБ, но и тем временем отметим следующее: в принципе, вы можете использовать формулу для корня алгебраического уравнения степени 4.
Любое из приближенных решений этого уравнения Но в этом случае нам понадобится так называемое первое приближение x. Читателя просят объяснить, почему это выражение найдено, например, при 4000 exp (-5x / 2) = 3205,43 (4.9)
В результате | x = In 1 .24788 = 0, 2216, поэтому сначала получим x = 0.08865, а затем уточним: 6 = 0, 09063 •
Смотрите также:
| Накопление и приведение. | Фундаментальные принципы. |
| Обычный процесс накопления. | Уравнение равенства стоимостей. |

