Оглавление:


Общий способ вычисления моментов инерции сложных сечений
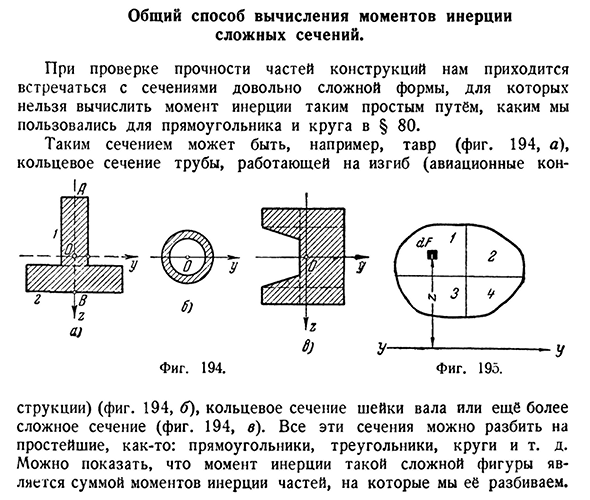
- Распространенный метод расчета момента инерции для сложных сечений. При проверке прочности деталей конструкции мы получаем сечение довольно сложной формы, которое невозможно рассчитать
моментом инерции таким простым способом. Такие сечения, например, Тор (рис. 194, а), кольцевая часть трубы,
работающая на изгибе (авиационное мошенничество Фигура. 194 рис. 19 градусов. Людмила Фирмаль
Структура) (рис. 194, б), кольцевая часть шейки вала или еще более сложная часть(фиг. 194, а). Все эти сечения можно разделить на самые простые: прямоугольники, треугольники, круги и т. Показано, что момент инерции такой сложной фигуры является суммой моментов инерции частей, разделяющих ее.§ 82] момент инерции
к параллельной оси 275 Возьмите (рис. 195) произвольная фигура, представляющая поперечное сечение балки; в ее плоскости рисуется ось y-Y. момент инерции на этом рисунке для оси y—y равен(13.7): Где z-расстояние от базовой платформы dF до оси Y. Разделим взятую площадь на четыре части F3 и F4. Теперь, при вычислении момента
- инерции по уравнению (13.7), мы группируем члены подфункции так, чтобы они суммировались отдельно для каждой из выбранных четырех областей, и значение интеграла не изменяется. Или F^дя=^З И Д Ф=^З И Д Ф^J в ГМ/7 4-й G9dF. Каждый из этих интегралов представляет момент инерции соответствующей части области
относительно оси y-y\so Jy=/y Jy J f/yV>(1 4.6), где fy-момент инерции относительно оси Y-y области. Результат можно сформулировать следующим образом: момент инерции комплексного числа равен сумме моментов инерции его составных частей.
Поэтому, например, для расчета момента инерции участка, показанного на рисунке. Для Людмила Фирмаль
194, b, оси OU необходимо найти моменты инерции прямоугольников и треугольников относительно оси OU и сложить их. Поэтому необходимо уметь рассчитать момент инерции любой формы для любой оси в плоскости. Решением этой проблемы является содержание данной главы.
Смотрите также:

