Оглавление:


















Общий случай движения твердого тела. Сложение поступательных и вращательных движений
- Общий случай движения твердого тела. Добавление поступательного и вращательного движения 1. Скорость тела в случае общего движения. Уравнение движения для твердого тела в общем движении、 Где x () y y (y z0-координаты любой точки выбранного твердого тела на полюсе.0, < p, 0-угол Эйлера: угол прецессии, угол чистого Офо или соответствующий угол для определения вращения твердого тела, вращения и оборотов вокруг полюса угла.
Скорость любой точки твердого тела в случае общего движения определяется по формуле 10) определить кинематический параметр винта, равный отношению минимальной поступательной скорости T, по следующей формуле; мин; угловая скорость полученного твердого тела p_v_rnin _ <* х > х + shuUy + < ЗВИ ’- — — И » O) O)- На даче 7.14. Свести пространственную систему сил к простейшей форме, и、 Добавление твердого тела поступательного и вращательного motion.
In в этом случае роль силы играет угловая скорость, а роль момента соединенной пары-поступательная скорость твердого тела. Людмила Фирмаль
Задача 7.14.Размеры тела показаны на рисунке, угловая скорость(О,,, 0) 2, C03 и G> i. Делать движение тела в простейшей форме, если в = В4 = 2У), о).2 = о) 3 = e. координатные оси показаны на рисунке. С точкой O в качестве центра торможения заданный набор угловых скоростей замедляется до скорости v и угловой скорости ω0 в общем случае. Определяет проекцию угловой скорости на результат. (6 *) ■r = — w, — w3 — | — w4-J-o) 4 = — 2o) — co -} — w -) — 2sh = 0, следовательно, вектор равен нулю: Да.) = В * Я + «я + * Л =В.
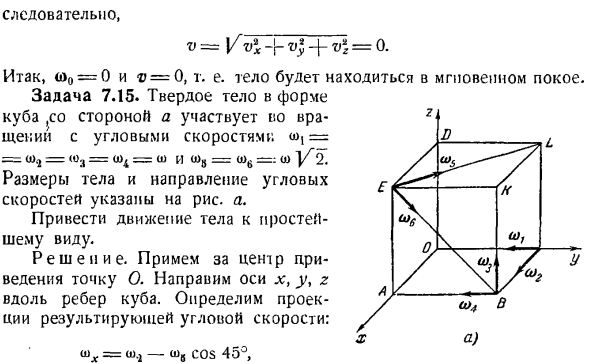
Найдена проекция результирующей скорости на оси vx, vy, vz, а также проекция основных моментов силы. 22а<*vvx =а>;. — (О3•а=: — — — <ОД == 0、 h’U = — < » 4•a-co3■a = — 2wd = 0、 Для этого + » ! + » != Ля Поэтому (o0 = 0 и v = 0.1, то есть тело будет находиться в состоянии покоя мгновенно. Задача 7. 15.Твердое тело в виде куба со стороной А соединяется, но вращается с угловой скоростью, причем с> 1 =(D. J = <0., = 0) 4 = W и 0) d= 0> 6 =:(1)] / Е2.Размеры корпуса и направление угловой скорости показаны на рисунке. один.
- Это придаст движению тела самую простую форму. Решение. Укажите оси X, y и z вдоль края Куба, а точку O в качестве центра сокращения. Определяет проекцию угловой скорости на результат. в = Вт.2-В8 Косинус 45、 0> v = — ω, — a> 4-|-0) eCOS45°-[- — Дж-4 в COS 45°, как WZ = В3-П)6 Косинус 45°. Замените угловую скорость. У нас есть: ==°> в=» > * = Поэтому в результирующем движении нет вращения. Определяет проекцию результирующей скорости трансляции. ЧХ =(o3a — <ви соз 45°-грех 45°, вы =—Косинус 45°о> 6 дней в COS 45°, ВЗ—ща-<В2-Джей.
(a6a от COS 45 ° грех 45°.Известное значение величия замещения мы получаем: б.) К здщс 7.15. = — Вау, vz = 0. ЧХ = — о)、 в. •- у В свою очередь, коэффициент поступательной скорости v = Vr = » и V2. Поэтому движение тела переводится сразу с указанной скоростью v = MaV2, как показано на рисунке. 6. Полезно отметить, что результирующее поступательное движение получается из сложения некоторых вращений. Задача 7. 16.Тело A вращается с угловой скоростью o>вокруг оси I, тело B независимо от угловой скорости w.
Дайте телу B дополнительное вращение с угловой скоростью-oy, чтобы тело B не двигалось. Людмила Фирмаль
вокруг оси II. вращается с 2 = 2<,.Ось II перпендикулярна оси/и удалена от нее. Как тело а движется против тела Б? Решение. Графический способ. Движение тела A против B суммируется Перейдите к задаче 7.16. Угловая скорость от вращения вокруг оси 1 При о| — Со от вращения вокруг оси II с угловой скоростью. и… Вектор-давайте совместно.»Точка а, то в этой точке, помимо вектора-со, скорость в = ГХ <* я> Где r = / M его вектор v / ведется вдоль оси и равен модулю в ЦО>. а = 2 (0 ^.
Сложив угловую скорость u и применив ее к точке A, получим суммарный вектор c, с осью I под углом и осью//с углом a4. Здесь можно сказать, что движение тела а к телу В состоит из вращения вокруг оси III с угловой скоростью. О)==(о, — е (02、 Численно равен О> = Г О) Ф = О).] / −5 Ось поступательного движения III скорости v составляет угол a (направление поступательной скорости v (рисунок B)). Когда движение уменьшается до спирали, вы можете визуализировать движение тела более четко.
Разложим скорость v на 2 взаимно перпендикулярные компоненты, v cosa и V sina (рисунок C).Компонент v cos a направлен вдоль вектора (o. < o перпендикулярная компонента v sin <*]может быть представлена в виде пары оборотов, в которых момент равен произведению угловой скорости плеча/. длина v sin al = < ol. Присвоить найденное значение V и выражение этого уравнения Аль. грех ИИ =- Вл + tg9 «я У нас есть: — =Уд•/、 Так… Где найти: Л._ \
Таким образом, относительное движение объекта состоит из вращательного движения угловая скорость W и поступательного движения скоростью v COS я по спирали небольшая(рисунок c).Тело а совершает спиральное движение против тела I. Модуль скорости перевода Я 2 в COS 04 =2®), а — = аа ^. В 5 г 5 Эта задача также может быть решена аналитически, как и то, как сделать пространственную систему любой силы, используемой в статике, простейшей формой.
Угловая скорость-это статический силовой вектор скольжения. Скорость трансляции-это свободный вектор, подобный статическому моменту. Метод анализа. Движение тела A относительно тела B состоит из 2 вращений: угловой скорости o, осевой / и угловой скорости-(o. 2, ось / / направлена в отрицательном направлении.
Если вы выберете координатную ось с точкой A в качестве начала координат, проекция угловой скорости результата на координатную ось будет выглядеть следующим образом: (к) Х =-а) =-2 <х) л а)г = 0,ojz =(Дж)1. (1) Результирующий модуль угловой скорости равен (e)= l / wj b-t- = найти проекцию поступательной скорости на координатные оси: bx = 0,vy = 0, v2-2do>. (2) Модуль скорости перевода в = 2ao>. o>и проверьте, образует ли v прямой угол. Ш•в = U в)
Существует wyVy + = 2ao). Как вы можете видеть, скалярное произведение этих векторов не равно нулю, поэтому они не перпендикулярны друг другу. Это означает, что тело совершает спиральное движение относительно тела. Найти уравнение мгновенной винтовой оси. Использовать выражения ЧХ-Зуй В.-2 <О -) — а <о, В2-Хиу г <* х (3) «У» Эта формула принимает следующий вид, учитывая формулы (I) и (2): в 2го)Т + вверх), _ 2а-2г 2 — 0 — 1- ’(4) Или Л — _ _ 4 Где v-скорость любой точки твердого тела. v0-скорость полюсов. < ю-мгновенная угловая скорость твердого тела. Г1-радиус-вектор от полюса до точки, определяющей скорость.
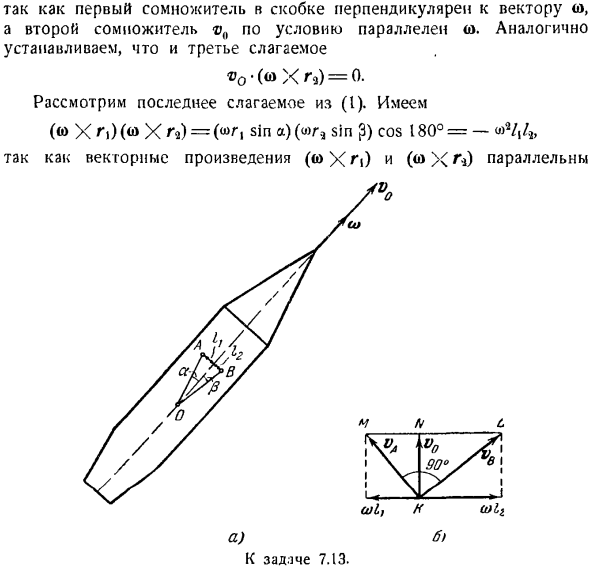
Ускорение любой точки твердого тела в случае общего движения определяется по формуле Вт = В0 + э х Т+(Д х » (®х г).(3 ) Где w-искомое ускорение точки. В0-ускорение полюса. е-мгновенное угловое ускорение твердого тела. Задача 7. 13.Центр тяжести ракеты движется со скоростью v0, а сама ракета одновременно вращается вокруг оси с угловой скоростью w(рис. 2 точки A и B расположены на расстоянии/ |на одинаковом диаметре, перпендикулярном оси, соответственно. И от последнего.
Какие условия должны быть соблюдены для дистанции? Кроме того, что делать, если вы знаете, что скорость точек A и 8 перпендикулярны друг другу? Решение. Задача может быть решена двумя способами: аналитически и графически. Первый способ. Движение ракеты соответствует общему случаю движения твердого тела, а ось спирали совпадает с осью rocket. In в общем случае движения твердого тела скорость точки определяется по формуле (2). Таким образом, ось вращения параллельна следующей плоскости.
Координатная плоскость XZ, разнесенная на расстояние y = 4-a О Затем формируют ось z и угол a, который определяется из уравнения tga1 = 2.It остается найти поступательную скорость, с которой тело движется вдоль оси spiral. Is определяется по формуле (5) ®мин= — — -; (6) (6) подставляя все значения с правой стороны, это выглядит так: М, N-1/5 «- Естественно, в обоих случаях результат один и тот же. Где v-скорость любой точки твердого тела. v0-скорость выбранной точки На полюсе. <о-угловая скорость твердого тела.
T1-радиус-вектор от полюса до точки, где определяется скорость. Любой эструс O на оси ракеты будет фиксировать скорость утечки A и B в качестве полюсов. 10а = во + Вт x П; vн = v0 в + Ф Где T1 и r2 — радиус-векторы точек A и Vy, взятые из полюса O. скорости vA и vD перпендикулярны друг другу по гипотезе. Условием перпендикулярности векторов является то, что их скалярное произведение равно нулю. ва-ВД = 0. Подставляя значение скорости в это уравнение, получаем следующее: (В,+(®ХС я)• — Джей — <®Х =0.Если вы откроете скобки, вы увидите следующее: vi +(®0.(W XGh)= 0. I) рассмотрим последний термин.У нас есть (с X)) (к) Х р <я)=(о> Р1 грех) (о) П9 грех), потому что 180°= -»> * /、/ * На ягодицах.]] 7.13.
И направлены в противоположную сторону. Вводя значения термов в уравнение (I), можно увидеть следующее: «O — <Λ| / 4 = 0, наконец, это выглядит так: Это условие, которому сегмент/должен удовлетворять、 2-й способ. Графическое решение этой задачи показано на рисунке. дано сложение скоростей точек A и B на плоскости, перпендикулярной b, AB.
Скорость vA состоит из взаимно перпендикулярных составляющих, равных (по модулю v0 и o)/.Аналогично, скорость vB берется из модуля, а далее o)/, причем компонент o> / 3 направлен в противоположную сторону, а скорости vA и vB взаимно Вертикальный. Тогда из прямоугольного треугольника МКЛ высоты КН、 КН * = Нм * НЛ ил и V \ = а> /. O> в / б Откуда? 2°.Добавление перевода твердого тела и вращательного движения.
Рассмотрим движение твердого тела, которое одновременно участвует в нескольких вращательных движениях вокруг оси момента, и нескольких поступательных движениях, расположенных произвольно. Вращательное движение твердого тела характеризуется мгновенным валом и угловой скоростью вдоль мгновенного естественного по. Вектор угловой скорости является вектором движения, поскольку он может быть перенесен в любую точку вдоль мгновенной оси.
Поступательное движение твердого тела характеризуется скоростью. Скорость поступательного движения твердых тел можно рассматривать как результат действия пары вращений. Скорость поступательного движения твердого тела является свободным вектором. Скорость перемещения добавляется в точке уменьшения путем перемещения вектора угловой скорости ®= gX(0, (1 *) Где r-радиус-вектор, проведенный от точки приведения вектора угловой скорости к приложенному теплу.
Таким образом, если выбрать любую точку за полюсами, то можно уменьшить все угловые скорости до этой точки и, кроме того, получить угловую скорость результата. о> =£(2 *) Поступательная скорость, возникающая при непосредственном задании или приведении угловой скорости к центру торможения, суммируется и дает результирующую поступательную скорость м. 0 = 2(3 ) к-1 Поэтому любое сочетание жесткого вращательного и поступательного движения может быть заменено 1 вращением дуги угловой скорости вокруг мгновенной оси через центр торможения и 1 поступательным движением velocity®0.
Дополнительные частные случаи вращения и поступательного движения твердого тела: 1. если o = 0, u0 = 0, гель мгновенно успокаивается. 2. если o> 0,1> 0 = 0, то тело вращается вокруг мгновенной оси. 3. если ыыы -\ — <> г. ВМ Ми.-
Смотрите также:
Предмет теоретическая механика

