Общий план исследования функций и построения графиков

Общий план исследования функций и построения графиков

• Общее планирование функции исследования и построения Как описано в предыдущем абзаце, вы можете выполнить качественное исследование функции и создать график. Качественное исследование означает исследование, которое позволяет найти существенные свойства функции, но не претендует, например, на точное значение функции. Вот несколько примеров таких исследований. Пример 1. Сюжетная функция ^ (‘-4); (* + 2) -и 1.

Все действия, показанные в правой части уравнения (), выполняются для значения независимой переменной x>, поэтому функция существует везде. Другими словами, область его существования -oo ± oo. v (х-4) 2 (х + 2) (х-4) 2 (х + 2), lim ——’— ■ = —oo; hm —— 1—- = -f oo. X-СО0 +00 0 3. Рассчитать первую и вторую производные. / = j {[(^ -4),] ‘U + 2) + (X-4) 1 (A: +2)’} = = 1 (2 ( -4) (* + 2) + (x-4) ‘} = / = TK (x-4) + -v (* -4) ‘] = -I [* -4 + x] = x (* -2). J 8 8 1 4 ‘1 «v» J 8

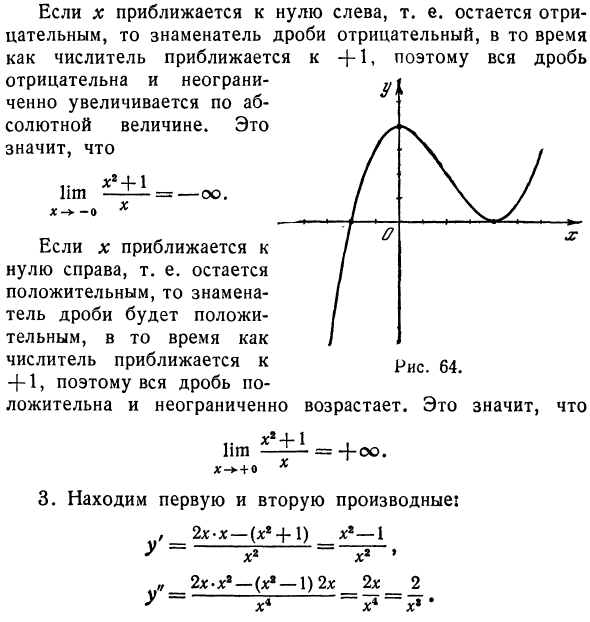
/ = 0; (д: -2) = 0, х = 5. Пронумеруйте важные значения в порядке возрастания. = = 2> = 4- 6. Создайте таблицу. X-00 <* <0 0 0 <x <2 2 2 <x <4 4 4 <x <+ oo Y ‘+ 0 — 0 «G — 0 + + + Выпуклый в возрасте. 4 выпуклые, зацените. 2 т. Вниз, вогнутый. 0-минутный возраст, вогнутый. 7. Создайте график (рисунок 64).

Найти критические значения для y ‘и y «. у ‘= 0; 3 * (* -4) = 0, х = 0, х = 4; Людмила Фирмаль

Пример 2. Изучение и построение функции Найдите область существования функции. Поскольку деление на ноль не имеет смысла, в область существования не входит x = 0. Другими словами, область существования состоит из двух частей: —oo <n: <; 0 и 0 <* <+ oo. Это означает, что график функции также состоит из двух частей. 2. Изучите поведение функции при приближении к границе удаленной части плоскости и области существования. Поскольку порядок числителя больше, чем порядок знаменателя (см. Главу 6, стр. 8), лим- ■ — = — оо, лим-! — = + оо. Х х X- + -00 L x-► + доступно

Если x приближается к нулю слева или остается отрицательным, знаменатель дроби становится отрицательным, а числитель приближается к +1, поэтому целая дробь становится отрицательной, а абсолютное значение увеличивается бесконечно. Это значит = Если x приближается к нулю справа, то есть остается положительным, знаменатель дроби положителен, а числитель приближается к +1, поэтому вся дробь положительна и неограниченна. г х * + 1. ЮЩИЕ! — = — (- оо. X X —► + O L

• 3. Найти первую и вторую производные. 2x-x- (xr + ) _ x- (y ~ x2 ~~ x2 » 2x-x2- (x * -1) 2x 2x 2 Рисунок 64 Это увеличивается. Это значит Найти критические значения первой и второй производных. а) отсутствует при y = x = 0; б) Y = 0; xi- \ = 0, * = ± 1; c) y «не существует для n; = 0; г) значение у «х не может быть равно нулю. 5. Пронумеруйте критические значения первой и второй производных в порядке возрастания. 6. При составлении таблицы отметьте в ней признаки производных и изучите ее особенности

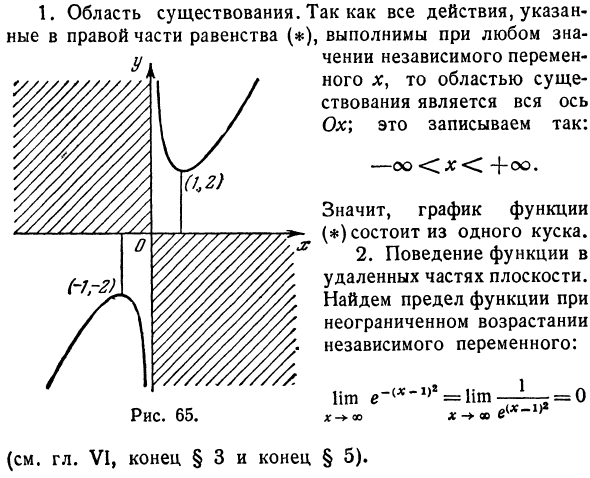
Затем найдите точки снижения, выпуклые и вогнутые, точки экстремума и перегиба: X-oo <x <—1 — 1- \ <x <0 0 0 <* <+ 1 +1 + \ <X <+ 00 Y ‘+ 0-Существительное. -0 + Y «— не существует. Выпуклый в возрасте. —2 проверить уменьшение, выпуклость. Это не существительное. Возраст 2 минуты, вогнутый. 7. Создайте график (Рисунок 65). Пример 3. Изучение и построение функции Существующая область. Поскольку все действия, показанные в правой части уравнения (), выполняются для любого значения независимой переменной, x} Существующая область — это вся ось Ox. Напишите так: —Oo ) состоит из одной части. Рисунок 65 2.

Функция поведения в отдаленной части самолета. Найти предел функции, где независимая переменная растет бесконечно. lim e ~ (* «» 1) 2 = Иш- G- * 00 X CO e (X-1g (См. Главу VI, конец § 3 и конец § 5). Найти предел функции, где независимая переменная уменьшается бесконечно lim = lim- = 0. -ооо ex ~ 1) 3. Найти первую и вторую производные. / = -2 (jc-1) r + 4 (x- = 2- <x-1) * [2 (x- ) r- ]. 4. Найти критические значения первой и второй производных. а) первая производная везде. б) Из y ‘= 0, -2 (x-1) <Γ (* -) 2 = 0; l: -1 = 0; x 1; в) Вторая производная везде. г) l [2 (Л; -1) * -1] = 0. 2 (x-1) ‘-1 = 0, (* _!)’ *

Установите y «= * 0 и решите полученное уравнение 2 Людмила Фирмаль

Пронумеруйте критические значения первой и второй производных в порядке возрастания. Xr = 1 2 ~, xr = 1, x, = 1-) 2 • 6. Создайте таблицу, которая помечает производные символы, таким образом исследуя существование увеличивающихся / уменьшающихся функций, выпуклых и вогнутых поверхностей и экстремальных значений. 7. Создайте расписание (см. Таблицу и рис. 66 на стр. 132).

Смотрите также:

Предмет высшая математика

Максимальные и минимальные значения функции	Связь между графиком функции и графиком ее производной
Выпуклость и вогнутость линии. Точка перегиба	Бесконечно малые величины