Оглавление:


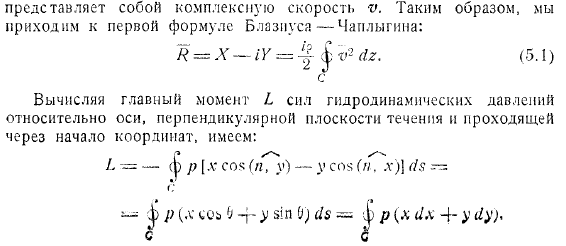

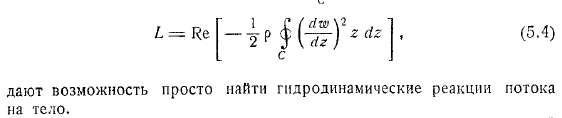

Общие выражения для гидродинамических реакций при установившемся течении. Формула Блазиуса-Чаплыгина
Рассмотрим основной момент гидродинамического давления, приложенного к неподвижному цилиндру любой формы при обтекании его в установившемся потоке несжимаемой жидкости, с установлением общей формулы основного момента гидродинамики. Кроме того, первый не делает предположений о наличии потенциала скорости, принимая во внимание только обтекание, без.
Аналогия с понятием комплексной скорости, учитывающей комплексное давление потока на объект и определяющей как зеркальное отражение основного отверстия гидродинамического давления от реальной оси, где внешнее нестационарное течение направление нормалей к телу, контуры и использование интегрального происходит вдоль контура тела в непрерывном потоке, при условии, что нет массовых сил, однако для непрерывного потока вектор скорости потока на контуре является касательным к контуру.
Формула Чаплыгина — выражение для вектора подъемной силы, действующей на обтекаемый контур. Людмила Фирмаль
- Следовательно, является комплексной скоростью. следовательно, вы достигаете первого выражения Бласиу. Чаплин: c расчет основного момента гидродинамического давления на оси, перпендикулярной плоскости течения и проходящей через начало координат: интеграла Бернулли повторного использования, становится. Как уже упоминалось выше.
Таким образом, мы доходим до формулы течения Блазиуса-Чаплыгина. Уравнение Блазиуса-Чаплыгина принимает вид в этом случае, если считать, что поток, обтекающий тело, является латентным, а аналитическая формула возможности вычисления гидродинамических реакций при установившемся течении комплексного течения известна. Позволяет легко найти гидродинамическую реакцию потока на объекте.
Если поток вне обтекаемого контура свободен от вихрей и источников, то комплексный потенциал регулярен вне и по теореме Коши в формуле Чаплыгина контур можно заменить любым контуром, охватывающим обтекаемый профиль. Людмила Фирмаль

