Общие рекомендации по вычислению пределов

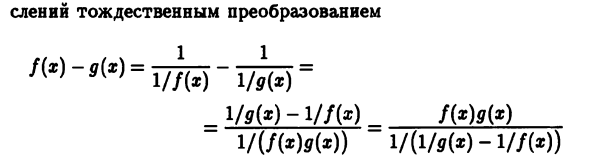
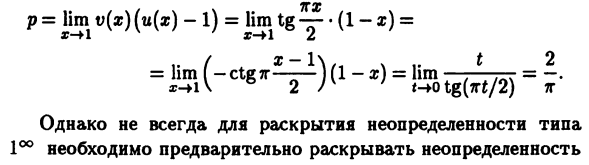
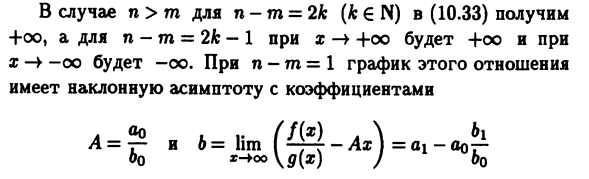
Общие рекомендации по вычислению пределов

• Расчет лимита является одним из основных Практическая задача математического анализа. Легко организовать Правила и методы расчета пределов функций Как уже упоминалось выше, вот несколько общих рекомендаций: 1. Используйте свойство непрерывности функции. бели — \ a непрерывно со знаком под знаком предела как x По функции f (i), тогда (9.1) \ imf (x) = f {a). В этом случае важно запомнить все основные функции Непрерывно в области определения и знает характеристики Функция, которая непрерывна в некоторой точке (см. 9.2). Пример 10.11. а.

Полином P2 (x) = x2-4x + 3 Поскольку он непрерывен в произвольной точке на числовой линии R, (10.30), limft (*) = фут (5) = 8. б. Для рациональных функций f (x) = (x4-x3 + x) / (x5 + 2) в Из-за непрерывности в точке x = 1 lim f (x) = f (1) = 1/3. X ^ TX с. Функция h (x) = (x2 + 1) x + 2 непрерывна Суперпозиция непрерывных функций. Следовательно, lim h (x) = h (2) = 54 = 625. 2. Используйте свойства b.m. И функция BB. часто Правила перехода к ограничениям во время арифметических операций

Функция не может быть использована напрямую для Ограничения на их использование. Людмила Фирмаль

Пример 10.12. а. lim (sin i) / i не может быть рассчитан х — тоже Чтобы применить правило для вычисления частного отношения (7.24), lim sin x не существует и lim x не конечен. «я тоже» Но х-> оо 1 / х это б.м. Функция, грех х- Она ограничена. Следовательно, в теореме 7.4 их произведение является функцией. Как pm x-oo и по определению 7.10 lim (sina;) / a: = 0. х — тоже б. Рассчитать 1 1 \ -1 ** — Зж + 2 / Правило расчета общего лимита (7.22) не применяется. Поскольку термины не имеют конечных ограничений, х-> 1 бб 7,5 функция 4 и ее общая Общий случай неопределенности. Но в этом случае 1 1 1 7 + -5- + х-2 Предпочтительный предел -1. 3. Раскрытие неопределенности.

Тип неопределенности 0/0 и 1 ° ° встречаются, когда вы думаете, здорово Ограничение (см. 7.7). Неопределенность типа OO / OO И oo-oo (или oo + oo) неизбежно, если вычислить с помощью (10.29) Асимптота графика коэффициента уравнения (10.28) Функция. На практике этот тип неопределенности также возникает. О, ах, 0 ° и oo °. Понял под раскрытием неопределенности Выполните такое идентичное преобразование В результате ограничения могут быть рассчитаны в соответствии с известными правилами. Большинство неопределенных правил существуют в отношении неопределенности. Введите 0/0 и oo / oo. Они связаны с назначением основной части.

• Функции после полудня и bb, т.е. заменить их на более простые Эквивалентная функция. Происходит, когда требуется неопределенность типа 0/0 вычислить предел отношения f (x) / g (x) к xth или x-> oo, a / (x) и d (x) сопровождают такое стремление к аргументу x Дневная функция. Основная сложность раскрытия Этот тип неопределенности подчеркивает основную часть этих функций Форма A (x-a) k как x- * a и Форма A / xk как x-> oo (в этом случае Вообще возможно). Согласно теореме 10.4, после замены Ниже предельного символа основного отношения отношение f (x) / g (x) Части и редукция с сопоставимыми x-a или g ItB (xa) ‘или lim Bx ~ l расчет достигнут. Они равны х ~ \ и я-ю B, если / = 0, 0, если /> 0. / <0, эти ограничения Стань бесконечным.

Пример 10.13. а. Найду км x- + o x2 sin2 x-x arctg x Под знаком предела находится общий коэффициент b.m. функция Как х-> 0. (10.18) и определение 10.2 x2 tgr2x = Qo (2×3) и x2sm2xx = Qo (x и Tctgx) Одна основная часть x- ¥ 0, числитель и знаменатель под знаком предела Таким образом, есть 2g3 и -zh arctan x, и w arctg x ~ x2.

В результате .. а? 2tga? 2 + 2а? 3 2а? 3 lim — zr = lim- = «= ~ 2 lim x = 0. о? 3 эм w-sarctgz o * o б. Рассчитать .. ln (l + 2a? + 3a? 2) + tga? х3 ЮЩИЕ 1 + 2а? — оригинал (10.18) С точки зрения 1n (1 + 2l + 3a? 2) r ^ o2x + 3l2. х2 = = o (x), 2x + 3×2π £ o2x. Для транзитивности активов Эквивалентность равна 1n (1 + 2π + 3×2) ^^ x. с того времени txxj ^ x и а? 3 = o (x), основная часть молекулы x- ¥ 0 2х + х = 3а? (10.18) -er-l ^ 0 «» main Знаменатель часть 1 + 2а? -ex = 2a ;-( ee? -1) с x- »0 2a? -х = х. В результате .. В (l + 2a + 3a) + tgaa3 .. Для? lim-2 # ° ​​= hm- = 3 # * + Приблизительно 1 * 2 * fO x

Неопределенность типа OO / OO также могут быть выявлены Основная часть подчеркнута, но сейчас она функциональна или На основании теоремы о связи 7.5. Людмила Фирмаль

И БМ функции свинца Эта неопределенность имеет тип 0/0. При расчете предела x- ¥ разница f (a?) — g (x) Или это так? -> Когда у оо, у f (a?) И q (x) есть такое желание Аргумент а? бб это функция, есть неопределенность Типа у-у-у. В зависимости от удобства после этого Вычисление преобразования личности Nx) ~ 9 (х) = мш ~ мш = Эта неопределенность может быть уменьшена до типа 0/0 или oo / oo. Будьте осторожны, чтобы удалить в некоторых случаях Неопределенность, как оо-оо в иррациональных выражениях Перемещая иррациональность в знаменатель. Если x-> a или x- * oo f (x) -b.m функция d (x) -bb, затем расчет предела продукта f (x) g (x) связан с указанным отсосом аргумента x • раскрытие информации о неопределенности типа 0. тождественность преобразование Может быть уменьшен до типа 0/0 или oo / oo.

Неопределенность типа 1 ° в расчете происходит Экспоненциальный предел (см. Пример 9.7) u (x) v (x) как x-> a или x- \ oo, если Аргументы x и (x) -►1, v (x) являются b.b. функциями. от (9.18) есть lim u (x) v (x> = expf lim v (x) lnu (x)). (10.32) Следовательно, неопределенность типа 1 ° Вычисляя предел произведения v (x) \ nu (x) Далее, связанные с раскрытием неопределенности типа С точки зрения (10.20), так как ω-0, u (x) -> 1 \ pi (x) -> 0 Теорема 10.4. При ограничении (10.32) \ pi (x) Заменить на выражение u (x) -1. Тип 0 ° неопределенности также возникает, когда: Вычислить границы функции (u (i)) «, но x-> a или x-> oo и (x) и v (x) являются b.m. Функция. тогда И (x) — »■ 0 lnu (s) — \ — ∞ и (10.32) предельные вычисления актуальны Раскрытие неопределенности типа 0 • oo. Неопределенность oo ° приводит к аналогичной ситуации,

Происходит при вычислении предела функции u (x) v ^ x \ x-y a или x-> oo и (x) и v (x) составляют 5,6 соответственно. И функция БМ. Где u (x) -►c \ pi (x) — * oo, и Опять же, неопределенность типа 0 • oo достигнута. Поэтому все типы считаются Уменьшить неопределенность из-за идентичных преобразований Два основных типа: 0/0 и oo / oo (или даже один тип Д / 0). Пример 10.14. Для расчета лимита лим (2-ар) * 8 ^ / 2) Связанные с раскрытием информации о неопределенности типа 1 °, Используйте (10.32) и установите u (x) = 2-x и v (x) = tg (? Rx / 2). lim (2-xy *** y = expflim tg ^ ■ In (2-x)). стоит? -4л \ х— \ л 2 / Экспоненциальный предел, то есть раскрыть Неопределенность, такая как oo • 0, заменить переменные,

Преобразование тригонометрических функций с Последующая замена соотношения б.м. Работает на них Эквивалентно (10.18) и теореме 10.4: pH lim tg — ln (2-s) = = hm (-ctg-J ln (l -1) = -lim —7 — rfr = -hm —-rr = -. \ 5 2 / v; t ^ o tg (Trx / 2) <-40 нт / 2 7G В результате lim (2- *) M0 ™ / 2) = e2 / ff. Тот же результат получен из (9.19). (10.18) и то же самое изменение переменных с учетом теоремы 10.4, Предварительно рассчитанные p = lim v (x) (u (x) -l) = lim tg- • (1-x) = = hm I -ctgTr —-— 1 (1-x) = hm —-— j ^ r = -. тг (нт / 2) Тем не менее, это не всегда раскрывает неопределенность типа 1 ° надо сначала выявить неопределенность

Введите oo-O, чтобы применить (10.32) или (9.19). в В некоторых случаях экспоненциальная функция Можно преобразовать в такой формат под символом ограничения, Основа для порядка u (x) и показателя степени v (x) Существуют конечные ограничения (см. (9.16)). Тогда вы можете Используйте напрямую (9.18). Например, при расчете lim (l + sinx) ctg * u (x) = (1 + грехи) 1/8111 * и u (x) = сож, С учетом второго существенного ограничения формы (7.42) х нс преступление ) 1 / Ein * = smx = T-> O х-Ig А для непрерывности функции cos i lim cos a? = -1 так X — Нет.

Следовательно, применительно к (9.18) b = e и c = -1. Желаемый предел составляет 6e = e «1 = 1 / e. Пример 10.15. Pn (x) = xn + a ^ 71 «1 + … + an и Qm (x) = boxm + b \ xm ~ l + … + 6m является полиномом n-го порядка, m (ntm € N), т. е. ao ^ O и bo ^ O. х-> оо Pn (x) и Qm (x) являются b.b. Функции и их отношения -lim -P ~ = Процессор! F 0 если n м. Для n> m, для n-m = 2k (k∈N) в (10.33) -l-oo, и n-mn = 2k-1 x-> + oo, если + oo и для x-> -oo становится -oo.

График этого отношения при n-m = 1 Имеет косую асимптоту с коэффициентами ff (x) \ 6i = -И 6 = lim ^ -T-f-Axe J = ai-oo7- b0 * — + oo \ g (x)) формула (10.28), которую легко найти из (10.29). Очевидно n = m, DaOx-Too (b *)) и h / W ^ eo ^ *) — При расчете их пределов при Pn (p) = 0 и Qm (a) = 0 Отношение x-> a достигает неопределенности типа 0/0. В этом случае полиномы Pn (x) и Qm (x) имеют вид Форма (см. 4.4) Pn (x) = (x-a) Γχ ()), Qm (x) = (* -a Где T ((x) — некоторый полином и Γ; (a) Φ0 (t = 1, 2). Мы будем учить ободок

Смотрите также:

Предмет математика

Сравнение бесконечно больших функций	Элементы теории множеств
Наклонная асимптота графика функции	Подмножества