Оглавление:





Общие понятия о концентрации напряжений
- Общая концепция концентрации Напряжение Уравнение для определения напряжений растяжения, кручения и изгиба, выведенное в предыдущей главе, состоит в том, что поперечное сечение представляет собой выемки или трещины в месте резкого изменения формы тела (подрезы, отверстия и т.), напряжение на краю отверстия, близкое к точке, в которой происходит приложение концентрации, напряжение вблизи углубления, место внезапного
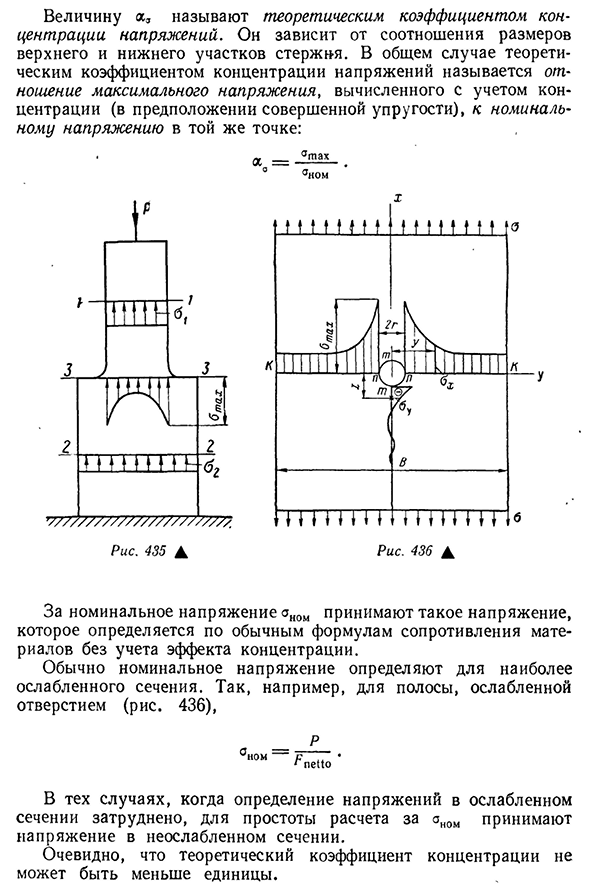
изменения В таких местах наблюдается явление резкого повышения напряжения, которое называется концентрацией напряжений. Так, например, при сжатии стержня (рис. 435), имеющие резкое изменение размеров поперечного сечения, напряжения сечений 1-1 и 2-2 можно определить по обычной формуле: Р И от 1 до 7? ‘°2-R2 ‘ где / 7! IG2-площадь поперечного сечения верхней и нижней части стержня. В секции 3-3 напряжение распределяется неравномерно, увеличиваясь к концу стержня и уменьшаясь к середине. Максимальное напряжение в этом разделе может быть
выражено как: °Шах — °г 525величину а называют теоретическим коэффициентом концентрации напряжений. Это зависит от Людмила Фирмаль
соотношения размеров верхней и нижней частей стержня. В общем случае теоретический коэффициент концентрации напряжений представляет собой отношение максимального напряжения, рассчитанного с учетом концентрации (при условии идеальной упругости), к номинальному напряжению в той же точке: Икс Но шах и Мистер … В случае номинального напряжения Аном принимает такое напряжение, которое определяется по обычной формуле сопротивления материала без учета эффекта концентрации. Как
правило, номинальное напряжение определяется для самой слабой части. Так, например, для полосы, ослабленной отверстием(рис. Четыреста тридцать шесть), # Ном Р Р Пейо Если определение напряжения в ослабленной части затруднено, то для облегчения расчета берется напряжение в неослабевающей части. Понятно, что теоретический коэффициент концентрации может быть не меньше его. Значение коэффициента концентрации напряжений 526 определяется методом теории упругости или экспериментально.
- Например, в теории упругости решение дается растянутой пластине, которая ослаблена круглым отверстием, расположенным на оси симметрии. Если ширина пластины B больше радиуса отверстия g, то самая слабая часть K-K (см. рисунок). 436) напряжение переменного тока определяется по формуле Здесь а-среднее напряжение поперечного сечения, которое находится далеко от места ослабления.y-расстояние от центра отверстия до точки, в которой определяется напряжение. Для U-g atah=. Итак, anom=a и AA=3. С увеличением Y напряжение быстро уменьшается и приближается к напряжению асимптотически. Точка t вертикальной платформы имеет сжимающее напряжение. Величина напряжения в вертикальном сечении определяется по формуле _(Zg4 да\2x4X* ) * В X=g AU= — a, X=2G AU= -^ -•, как видно из графика (см. рис. 436), эти
напряжения быстро затухают. Указанное выше точное решение может быть использовано только для пластин с большей шириной по сравнению с диаметром отверстия (B>. 10г). Когда ширина пластины становится небольшой, теоретический коэффициент концентрации напряжений становится большим, а напряжение на внешнем крае пластины (точка K, K) становится меньше, чем a. За столом. Приведены значения теоретического коэффициента концентрации напряжений для различных значений отношения диаметра отверстия 19 к ширине пластины. Т а б л и Ц А19 2Г / ВТ = 0 2Г / ВТ = 0.1 2Г/ВТ—0,2 2/76=0.3 2/76=0,4 2/7 6= 0,5 3.00 3.03 3.14 3.36 3.36 3.74 4.32 527как видно из таблицы, при = 4G А3=4,32.
Напряжение на внешней кромке пластины в этом случае равно Ah=0,75 O. Большинство задач Людмила Фирмаль
определения коэффициента концентрации методом теории упругости не решаются из-за его сложности, и образуются некоторые отверстия и полости (с обеих сторон или круговые полости).、 Во всех остальных случаях закон величины коэффициента концентрации и распределения напряжений по сечению экспериментально, т. е. методом фотоупругости, тензометрическим методом, направлением движения лакокрасочного покрытия при определении коэффициента концентрации во многих задачах прочности материала, очень выгодно использовать гидродинамическую аналогию. Поэтому задача распределения напряжений при растяжении стержня математически является задачей распределения скоростей идеальной жидкости,
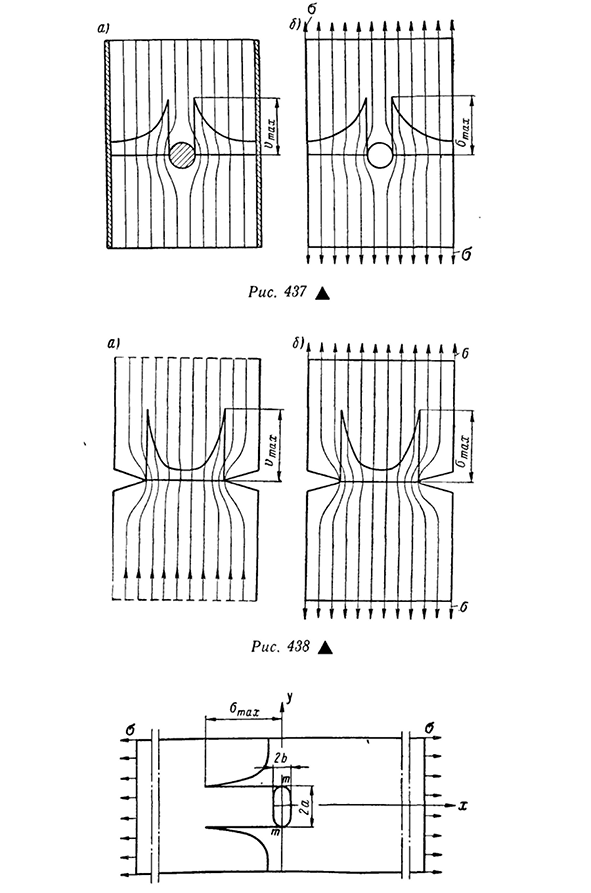
движущейся с постоянной скоростью в контейнере с таким же поперечным сечением, как и у растянутого стержня, и эта ситуация обусловлена тем, что дифференциальное уравнение силовой линии при растяжении совпадает с уравнением обтекания жидкости. «Если стяжная тяга ослаблена каким-либо отверстием или канавкой,то распределение силовой линии имеет ту же форму, что и распределение потока жидкости в сосуде того же поперечного сечения, эти дефекты должны иметь форму неподвижного выступа той же формы, что и ослабление растянутого стержня. Для риса. 437, а в виде вертикального цилиндра показано изображение потока
жидкости, движущегося через барьер и канал. На этом же рисунке показан график распределения скоростей в ограниченном сечении. Для риса. 437,6 представлен ослабленный призматический стержень в виде круглого отверстия того же диаметра, что и преграда в канале. На этом же рисунке показан локус напряжения и график нормального напряжения в месте ослабления разреза. Из сравнения цифр, рис. 437, а и 6, видно, что закон распределения скоростей идеальной жидкости в сосуде и закон распределения напряжений в стержне, ослабленном отверстием, согласуются. Для риса. 438 каждая линия подачи жидкости (фиг.Покажите закон распределения 438, а) и траекторию напряжения (рис. 438,6), а также график скорости и напряжения
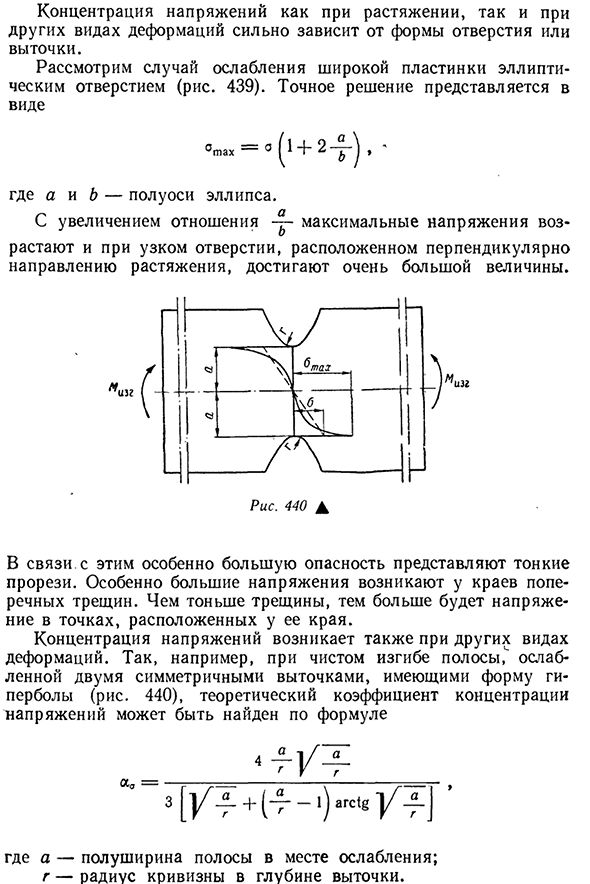
поперечного сечения, ослабленного депрессией. 528 страниц. 439 концентрация напряжений как при растяжении, так и при других видах деформации во многом зависит от формы отверстия или углубления. Рассмотрим случай, когда широкая пластина ослаблена овальным отверстием(рис. 439). Точное решение выражается в следующем виде °tach=0(1+2-y Где a и B-полуоси эллипса. При увеличении коэффициента максимальное напряжение возрастает, и в узком отверстии, перпендикулярном направлению натяжения, оно достигает очень большой величины. Рис 440Л. В связи с этим особую опасность представляют тонкие щели. В частности, большое
напряжение возникает на краях поперечных трещин. Чем тоньше трещина, тем больше напряжение в точке, расположенной на ее конце. Концентрации напряжений возникают и при других видах деформации. Так, например, в чистом изгибе полосы? Ослабленный двумя симметричными углублениями в виде гиперболы (рис. 440), теоретический коэффициент концентрации напряжений можно найти по формуле АСТ= 3[/4+^ -‘) AGS ‘ 8 / ^ > Здесь a-половина ширины полосы в точке ослабления, а g-радиус кривизны на глубине углубления. Поскольку только кривизна дна впадины 530 оказывает большое влияние на коэффициент концентрации, одна и та же
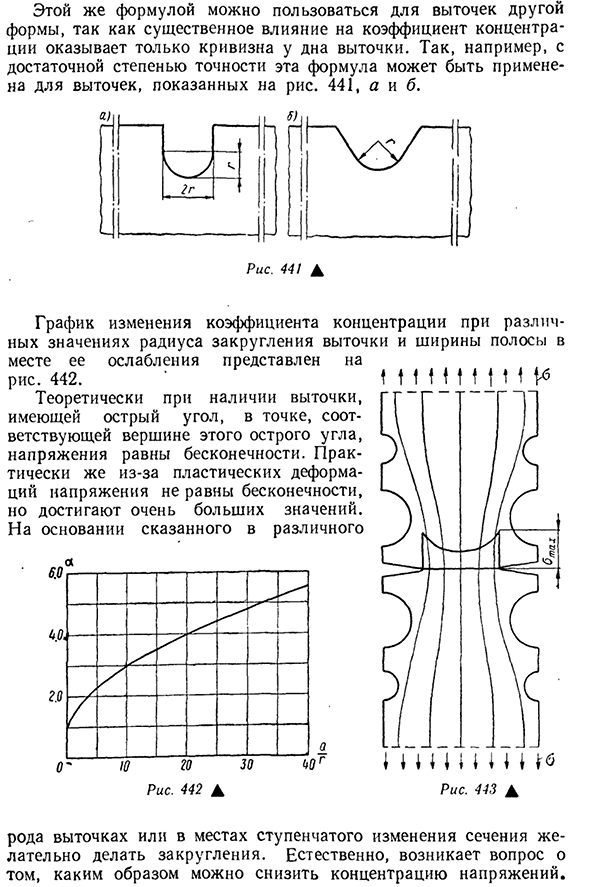
формула может быть использована для полостей различной формы. Например, с достаточной точностью эта формула может быть применена к надрезу, показанному на рисунке. 441a б График различных значений радиуса скругленных углов углублений и изменения коэффициента концентрации при их ослаблении представлен на рисунке. Четыреста сорок два Теоретически, при наличии углубления с острым углом, в точке, соответствующей вершине этого острого угла, напряжение равно бесконечности. На практике из-за пластической деформации напряжение не равно бесконечности, а достигает очень высокого значения. Основываясь на том, что было сказано в статье Рис 443А И пропускная способность в В месте ступенчатой смены выемки или секции желательно сделать круг. Естественно, возникает вопрос о том, как снизить
концентрацию стресса. 5311 1_1 Рис 444А For.to для уменьшения коэффициента обогащения необходимо заменить острые углубления плавными кривыми или, если позволяют конструктивные соображения, добавить дополнительные углубления, как показано на рис. 443. в этом случае поток напряжений выравнивается и, таким образом, коэффициент концентрации уменьшается. Чтобы остановить появление трещин в пластине, достаточно сделать отверстие на краю трещины,что значительно снижает коэффициент концентрации. Для пластмассовых деталей диапазон текучести считается неограниченным (см. Рисунок). 233), концентрации напряжений ниже статической нагрузки не опасны и могут вообще не приниматься во внимание. Это связано с тем, что максимальное напряжение в точке концентрации, которое достигает предела текучести, перестает увеличиваться, и текучесть материала
распространяется на все остальное. Дальнейшее увеличение нагрузки приводит к распространению текучести на глубину сечения, то есть происходит выравнивание напряжений в ослабленном сечении(рис. 444). Для хрупких материалов необходимо учитывать концентрацию напряжений даже при статическом приложении нагрузки путем введения соответствующих коэффициентов концентрации. В этом случае, когда ослабленная деталь достигает максимального напряжения, равного величине предела прочности s, появляются трещины, которые быстро развиваются и разрушают деталь. Следует отметить, что по мере того, как материал становится более хрупким, риск концентрации напряжений значительно возрастает с понижением температуры. Концентрация напряжений особенно опасна при действии нагрузок, вызывающих переменные или переменные напряжения. В этих случаях необходимо рассматривать как пластичные, так и хрупкие материалы, о чем будет подробно рассказано в главе xviii*. История
Смотрите также:

