Оглавление:
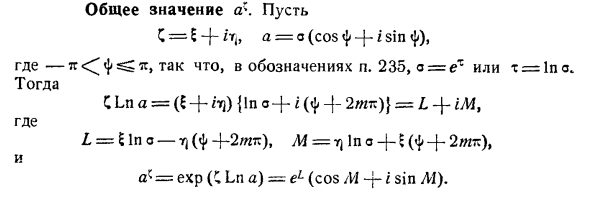

Общее значение а
- \ Итого С = S + ирита = о (потому что -фин <J <), Где-в разделе 235 обозначений, о = е ~ или х = 1о. тогда CLn a = (l + i-n) {In o + i — [- 2 = L + iM, где Z. = £ In ° -Yj + 2 / мкм), y = yj In a + E + и a ′ = exp (C Ln a) = ^ (cos / And sin L1). Таким образом, общая ценность c-In’-I (H2m «) [CQS ln Cf 2W7T)} -f- -f-isin jr ^ ln o-f- £ (ф + 2jmic)} J. В общем случае a ‘является бесконечной функцией. конечно 2 м *)
Если r (φ0.if y) = 0, оно имеет различное значение для каждого значения m>, и модули всех различных значений a равны друг другу. Людмила Фирмаль
| Показательная функция | Выражения синуса и косинуса через показательную функцию |
| Общая показательная функция | Обобщенные гиперболические функции |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Однако, если амплитуды не равны или разница не кратна 2tf, эти два значения будут разными. Для совпадения этих двух значений c) и £ (m и n — целые числа, m> bn) должны быть разными. Несколько и развалится \ (Φ + 2м) -% (φ + 2мз) = 2кн, В этом случае $ = ––– должно быть разумным. CL-Besko-gр-л Бесконечно, если C не является действительным рациональным числом. С другой стороны, значение действительного числа и рационального числа a в C конечно. Основное значение = exp (CLna) является основным значением Lna, то есть значением, полученным с использованием m = 0 в общей формуле.
Таким образом, главная ценность ag e-1n 0 до ^ {cos (t) ln c + 6 f) + i sin (rj In z + ft)}. Два конкретных случая особенно важны: Если a на самом деле является n положительным и C является действительным, c = a, 6 = 0, 6 = C, 4 = 0, основное значение равно <?: 1pa, то есть Ch. Соответствует значению, определенному в. IX. Если | a \ = 1 и C верно, o = 1, S = C, h = 0, а основное значение (cos6 -ji sin6) равно cosС ^ — {- / sin
Это дальнейшее добавление к теореме Моава Обобщение (ссылки 45, 49). Людмила Фирмаль

