Общее управление динамики системы материальных точек

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

Общее управление динамики системы материальных точек

Общая формула динамики системы масс При движении системы материальных точек, подчиненных идеальному сиянию, сумма работы инерционной силы с заданной силой и возможного перемещения точек системы равна нулю. н ^(Фу-mkwk) * БКК = 0. Я Если FkFk J FkyJГFkzb, Wk = XJ 1 1 * foJ-r * rk = + by J + b; kk、 Потому что нет необходимости вычислять сумму работы внешних сил и внутренних сил, которые являются силами реакции идеального сцепления. Если все наложенные на систему сопряжения

не идеальны, то необходимо дополнительно вычислить сумму рабочих сил Rk реакции неполного сопряжения и использовать теорему в следующем виде: Гамма, — гамма,= A A (Fk)+ 2 n (.). А = Я = 1 Задача 389.На внешнем зубчатом колесе имеются 2 шестерни радиуса r и g2 1 и 2.Момент инерции колеса относительно оси вращения равен J0l и 10 10, соответственно. Определите угловое ускорение колеса / крутящий момент, если к колесу приложена пара сил mQ. Игнорируйте силы сопротивления. Решение. Пара зубчатых колес представляет собой систему с 1 степенью свободы, так как положение 2-го колеса определяется углом поворота 1-го колеса.

Направьте ось z перпендикулярно плоскости проходящей фигуры. Людмила Фирмаль

Гравитационная скала колеса обозначается через P {и P.Обозначим данную силу: I,, Pb — пара сил, приложенных к колесу/с крутящим моментом I0. Голы 389. возьмем инерционную силу массы, входящей в систему n. При вращении колеса вокруг неподвижной оси его инерционная сила уменьшается до пары сил, равных по величине произведению момента инерции колеса относительно оси вращения и соответствующего момента инерции относительно модуля соответствующего выступа. Проекция углового ускорения связана видимым соотношением G1 * 1g = — G#и(1） (Из-за того, что колеса

вращаются в разные стороны, вводятся минусы.) Момент силы инерции пары колес 1 равен Момент силы инерции пары колес 2 Или рассмотрим Формулу(1： Дайте колесу возможный угол displacement. In в этом случае колесо 2 получает возможное угловое смещение b ->.А соотношение можно легко получить с помощью возможного смещения точки контакта K колеса<5g. ведь точка K принадлежит обеим шестерням、 БТ = TjEf | = Р = — gDR4 (Возможные угловые перемещения направлены в разные стороны, поэтому вводится знак минус), где &?* =- г Для составления уравнений общей динамики необходимо вычислить сумму работы заданной силы и силы инерции на возможное смещение точки системы, а затем уравнять эту сумму

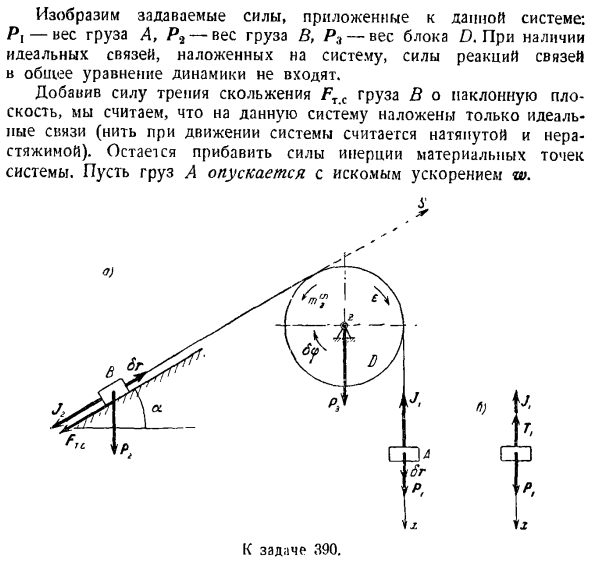
до нуля. ««0 ** 1 + 3 < Pi +» Щ= (Действие гравитации P1 и P9 равно нулю. Потому что точки действия этих сил не двигаются.） После использования формул (2), (3) и (4) уменьшить уравнение на < b слагаемыми: (4 )） Здесь мы определяем проекцию требуемого углового ускорения шестерни на ось z/： е Проблема 390.Определите ускорение w груза A и B, которое будет рассмотрено в задании 368. Solution. To решая задачу 368 с помощью метода кинетической статики, для определения ускорения нагрузки w необходимо было учесть 3 массы системы (нагрузка D, нагрузка B, блок D) по отдельности, составить»равновесные» уравнения этих масс и решить систему уравнений sin, включающую 3 неизвестных. Эту задачу можно решить гораздо проще, применив уравнения общей

динамики. Вместо системы уравнений, вам нужно решить только 1 уравнение. Укажите ось z вдоль оси вращения блока D на рисунке. Покажем заранее заданную силу, приложенную к этой системе: P1-вес груза A, P2-вес груза B, а R1-вес блока D. Если система перекрывает идеальную связь, то силы реакции связи не включаются в общее механическое уравнение. Если добавить силу трения скольжения Frc нагрузки B на наклонной

Радиус блока обозначается буквой G. Людмила Фирмаль

плоскости, то предполагается, что на эту систему накладывается только идеальная муфта (при движении системы считается, что нить растягивается и не растягивается).Добавление силы инерции материальной точки системы остается. Снизить нагрузку на нужные ускорения В. С. Да.） восемь лет \ ля Л В Четыре Я Четыре Четыре К выпуску 390. Приложите полученную инерционную силу к движущимся вперед грузам A и Wu и сориентируйте их в направлении, противоположном ускорению соответствующей

нагрузки. То есть, J1-вверх, а Y9-параллельно плоскости вниз. АВ = =(1） Приложите главный момент инерции напротив знака к блоку D, который вращается вокруг неподвижной оси Знак проекции углового ускорения e： «/’=- /ля. 1.г р * г * WX с 7 ^ = — ^ — от. И e ^ = y, то

(Основной вектор силы инерции блока VlJ)= — Mwc равен нулю. Это связано с тем, что центр тяжести блока находится на оси вращения.） Мысленно остановите систему и дайте 1 из ее ключевых точек возможный ход. Вы можете сообщить о линейном движении вверх и вниз груза A, или о движении вверх и вниз груза B-наклонной плоскости, или о возможном движении блока D-по часовой стрелке

или против часовой стрелки. Дай груза на возможное движение вниз по вертикали ЛБ. (Не следует предполагать, что направление движения какой-либо важной точки и ее возможное движение обязательно должны совпадать. Направление движения точки зависит от системы приложенных к ней сил, но в данном случае оно произвольно.)В этом случае из-за отсутствия удлинения резьбы нагрузка B получает возможное перемещение коэффициента изоупругости, который направлен вверх по наклонной плоскости, а блок D получает возможное перемещение угла. E&P. получает точку

резьбы на краю блока, чтобы получить отношение между линейными и угловыми возможными перемещениями БТ = р & р, (3)） Где r-радиус блока. Примените уравнение общей динамики к этой системе материальных точек. То есть сумма работы силы инерции относительно возможного смещения точек данной силы (включая силу реакции несовершенной связи) и системы равна нулю Pfir Дж \ приемопередатчик XBR п-п * БР грех-FrJr + жор =0.(4 )） Значение силы трения Fr C-fN = / Pa cos A подставляется в уравнение (4), используя уравнения (1), (2) и (3), или Pi—wx-Pi sin a — / P9 cos a — ^ = 0, Где найти искомое ускорение груза A W B предсказание： w-2gPt-P2 (sina + / ω$ a) (Ы в случае wx> Qy, то есть в случае P> P2 (sin a-f- / cos a), ускорение

нагрузки направлено вниз. Если, в зависимости от состояния задачи, необходимо также определить силу реакции муфты или давление на муфту, то к муфте должен быть применен принцип высвобождения™, сила реакции требуется для оплаты, и основной закон динамики или статический закон движения должны быть применены к соответствующей массе системы. Если есть расчетное ускорение, то это не сложно. Так что если вы хотите определить силу

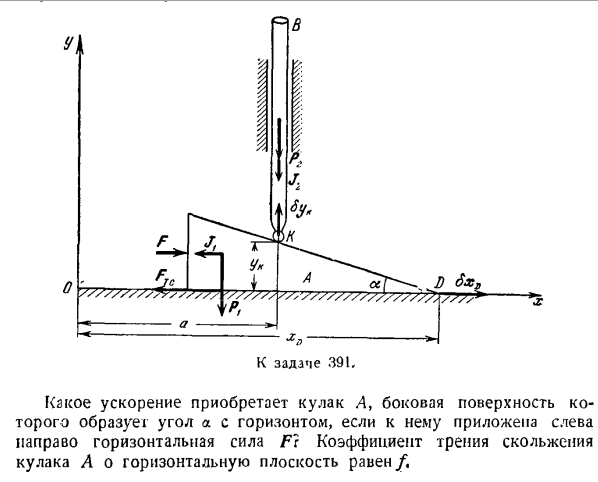
реакции, то правильную нить ветвей, мысленно срезаем NIG рядом с грузом, прикладываем к грузу 3 силы\ PX-вес груза, Техас(см. Рисунок б. — .Сила реакции пряжи, y, силильная инерция нагрузки. Напишите уравнение «равновесия» для нагрузки L, спроецированной на вертикальную ось X. П> — Ц + Jljt = 0. Для {PD внедорожник / пикап = — WX с} г ТХ = РХ-й Wjrf Где wx-ускорение нагрузки, определяемое уравнением (5). если вы назначаете wx, это выглядит так: Т-п | / па + 2Р«(л 4-Син г — | — / коза)л 1- ’ ИС, Н-значение 2pt +Рь Задача 391.As вес px кулак a перемещается по горизонтальной плоскости с правой стороны, вес P9 стержень B поднимается в вертикальном рельсе. Если горизонтальное ускорение F1 применяется слева направо, то кулак-

это то, что ускорение. Коэффициент усиления 4, а его стороны образуют угол а относительно горизонтали? Общее уравнение динамики принимает вид н Х К ^ Х-«А)±» А)Б А +〜 «А)= 0. Уравнения общей динамики аналогичны принципу возможных перемещений в случае движения материальной точечной системы. Как вы знаете, когда система движется, сила реакции связывания обычно переменной. Они становятся функцией времени, координат точек масс, скорости, ускорения. Поэтому при решении обратной задачи динамики, в которой движение определяется заданной силой, необходимо исключить силу комбинированной реакции из комбинированного уравнения движения. Большое преимущество общих динамических уравнений по сравнению с другими

динамическими теоремами состоит в том, что в их формулировке отсутствует идеальная сила реакции связи. Если не все соединения идеальны, например, если существует связь трения, то, применяя уравнение общей динамики, к данной силе должна быть добавлена сила реакции, соответствующая неидеальной связи. Расчет величины работы силы инерции относительно возможного смещения точки

твердого тела осуществляется по формуле： а)в переводе： 8 А = Н (.) — Б、 Где R J-результат действия силы инерции (R’j] =-Mw w-ускорение любой точки твердого тела), либо-возможное смещение ярма твердого тела. б)при вращении вокруг неподвижной оси：

Решение. Рассматриваемая система имеет 1 степень свободы, поскольку положение кулака а на горизонтальной плоскости определяет положение стержня В. На рисунке показаны неподвижные оси xy. Заданное усилие прилагается к системе: P {вес кулака, P2-вес штанги, F-привод force. To к указанной силе добавим силу трения скольжения FTC кулака а в направлении, противоположном движению кулака, то есть по горизонтальной

плоскости, направленной влево. Применяют инерционные силы массы рассматриваемой системы. Так как кулак а и стержень в движутся постепенно, то к каждому прикладывается объединенная сила инерции, направленная в противоположную сторону к ускорению данного твердого тела, равному произведению величины, массы и коэффициента ускорения. Указывает на абсциссу точки D кулака x0 (см. рисунок), а ордината точки K стержня

представлена xD. (1） Ык =(х0-а) {£а> Где a и a-постоянные значения. используйте производную времени 2-го порядка yk для определения зависимости между проекцией стержня и ускорением кулака. (2） Если ускорение кулака а направлено горизонтально вправо, то ускорение стержня В направлено вертикально вверх. Таким образом, проекция на ось x результирующей 1-й силы инерции Jx задается формулой: А проекция на ось комбинированной инерционной силы стержня равна、 К = —РК = — Рамос ^ а — <3）

Кулак A дает bx0 возможную горизонталь movement. In в этом случае стержень B, bk может двигаться вертикально вверх. соотношение между bxn и bk определяется изменением Формулы(1). бык = bxDtg *. ■(Ля） Общее уравнение динамики этой системы составляет. То есть уравнять сумму работы заданной силы, силы трения и силы инерции с возможным смещением точки системы к нулю. GMO * h J \ x * xD-I-(Г1Х) Х+^ ^ Ук-Hjb ° YK = °> Куда? Ста = — fн = — Ф {ПЛ+ Рb + со,\ что FX =

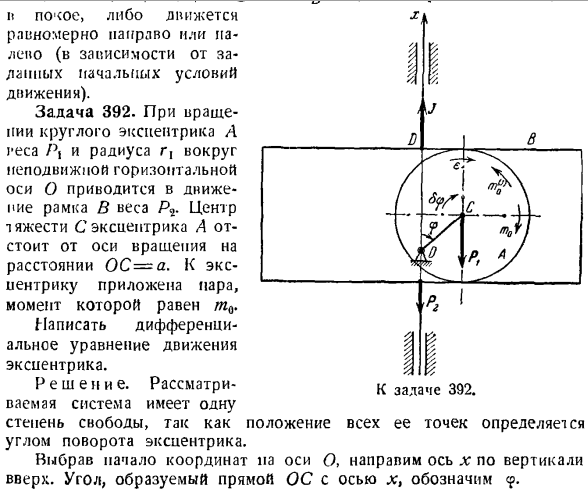
Ф Пий = — яме, р*, г = — п <л. Используя формулы (: j) и (4), после кратковременного сокращения уравнения на bx0: F-г * п + РП + Дж(г*) — р * ТГА-в J0.Где определить искомое начальное ускорение： О + / > — < / + тг а) тг «’ От наивного выражения лица、 А) F> /(P,-P-9)+ P4tga, то есть ускорение кулака а направлено вправо; Б) 1: .) = Pxa sin <p и P $ x = — P2, воспользуемся формулами (1), (3) и (4) для получения искомого дифференциального уравнения эксцентрического движения после редукции 8 <p. [Пи (р * — ф-2А5)+ 2 / х sin2 <Р]? — Дж.- + П ^ г грехов 2 <п-2г(ПЛ 4-Р2) грех <п-2 У = 0. Задача 393.Масса Pj и радиус RJ на оси c ролика a, масса P4 и

Радиус Р4.Некоторая сила приложена к блоку B в момент t(Y. In в этом случае нить обматывается вокруг края блока в, который вращается вокруг неподвижной оси, и кагку а катится вверх по наклонной плоскости угла а относительно горизонтальной плоскости, не скользя вверх. Определить ускорение центра тяжести ролика на наклонной плоскости, если коэффициент трения качения ролика равен/ К.

ролик А и блок Б считаются однородными круговыми дисками. Масса нити игнорируется. Решение. Рассматриваемая система имеет 1 степень свободы. Это происходит потому, что положение, заданное углом поворота блока B, определяет положение ролика A. Указывается установленная сила: Р, — масса ролика а, Р4-Масса блока в, 2 силы крутящего момента rnQ. Наклонная поверхность, по которой катится ролик а, не прилипает к идеальной адгезии.

Поэтому к указанной силе прибавляют силу трения ролика о наклонную плоскость (F ^ = FN = fPx cosa), направленную вниз вдоль наклонной плоскости (/- коэффициент трения скольжения).Из-за трения качения нормальная реактивная сила R на наклонной плоскости смещается в сторону движения ролика на расстояние/ k, равное плечу трения качения pair. TK = RfK = fkPrcos a. Рассмотрим инерционные силы системы. Направьте оси z и l перпендикулярно плоскости фигуры от траектории. — Вдоль нити. Ускорение wc центра тяжести ролика направлено параллельно линии максимального

наклона наклонной плоскости. Поскольку поток расширяется, wCx = ^ r ^ 2.Если ролик перекатывается без скольжения, то мгновенный центр скоростей находится в точке соприкосновения с наклонной поверхностью ролика, поэтому расширением WCX = rxsl2t. Где S-проекция углового ускорения ролика. Так… > > СХ = г1 * \ Р = Т&Р(1） В блоке Wu, который вращается вокруг неподвижной горизонтальной оси Oy, перпендикулярной плоскости фигуры, мы применяем пару сил инерции момента t { / }\, который имеет противоположный знак углового ускорения проекции e2z. < > = — ’ов Блок Круглый и однородный R g- Привод, g. e.= get： <=(2) «о Сила инерции ролика а, совершающего плоское движение, сводится к силе, равной основному вектору V (y), и к паре сил, где момент равен основному моменту.

Инерционная сила V1 ^приложена к центру тяжести c ролика и направлена в противоположную сторону к ускорению wc В(к)= — ^ WCX находился. (3） Основной момент инерции относительно оси с через центр тяжести ролика, перпендикулярный плоскости симметрии материала, r^, имеет знак, противоположный проекции углового ускорения е, 2-ролики.= — рассмотрим lQ-P r2 = Писать： Где tu-ось вращения z (///’l = = — / e. It является «первичным» моментом инерции относительно А) возможного углового перемещения

твердых тел. в) случай плоского движения： Где V1 ^ — вектор инерционных сил (V {} — Mwc wc-ускорение центроида твердого тела), mc} — главный момент силы Инерция вокруг оси через центр тяжести твердого тела перпендикулярно плоскости составляет 100 материи!! Симметрия (m ^ = — / C£r), bc-возможное смещение центра тяжести c твердых тел. — Возможно угловое смещение твердого тела. Используя уравнение общей динамики, можно решить задачу динамики точечной системы, что важно в следующих случаях: Таким образом, сила инерции этой системы сводится к 1 набору сил

момента m ^(блок B) и к 1 набору сил момента V ^(звено A). Дадим блоку возможное угловое смещение Scp9. при эюм, точка нити на ободе блока, получает возможность движения данные^®2.В связи с не растяжимости нити, центр тяжести звена имеет те же возможные перемещения: ОГК = r88 4 4. Так как точка&является центром мгновенной скорости ролика, & rc = r, 5’3, где B -; — возможное угловое движение ролика a. (5） 8rc = Р&?Я = re8 <Р3. Создайте общую формулу динамики рассматриваемой системы. t0b-П \ БРС грех + \ «4rQ + + + / лм> к 8?,+ 3Л (фтп)+ ОА (Пн)= 0 Точка действия этой силы неподвижна, поэтому работа силы тяжести Pq равна нулю.

Теперь выберите фактическое смещение d в качестве возможного смещения (cof. Вы можете сделать это, потому что 3H является стационарным).При реальном перемещении сила трения 8L (/7tr) работы сводится к нулю, поскольку точка приложения силы трения всегда совпадает с мгновенным центром скорости. если учесть K = — kKR = — / kPi C°s a и использовать Формулы (2), (3) и (4), то можно увидеть следующее: Госкомзем Р, Гг — Ви?»- Водонепроницаемые-П ^ РЦ грех * — Джей wcxK потому что А <Б= 0. Используйте выражения (1)

и (5) для выражения fy, o-f4 в виде bc, zl2 и^в wCx. после сокращения каждого члена уравнения на bc: 77-г—грех-й туалет * х -^»»» = Здесь мы определяем проекцию требуемого ускорения центра тяжести ролика а на ось X. Шл(Ф \ — П (грех-я） — з-пп ^ — А. If> Pi fsin a-j — ^ cos aj, nvCx ^ > Oy, то есть I> c, направлен параллельно линии максимального наклона наклонной плоскости.

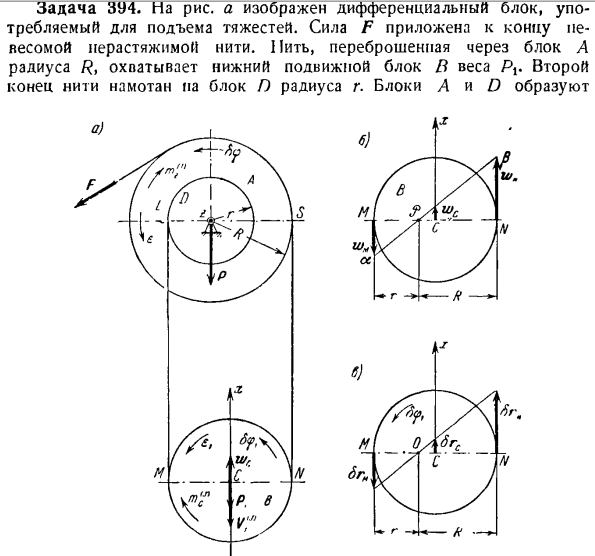
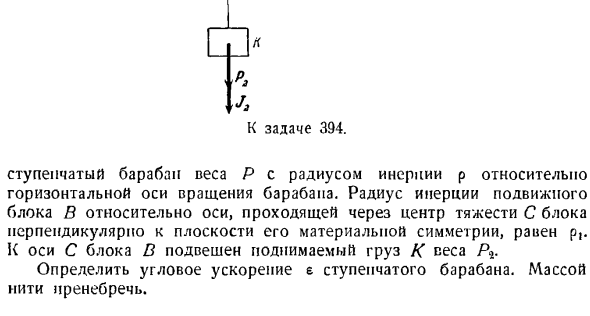
Задача 394.It показывает дифференциальный блок, используемый для подъема тяжелых предметов. Сила F прикладывается к концу нити, которая не растягивается в невесомости. Я! Линия, проходящая через блок a радиуса R, охватывает Нижний подвижный блок B веса P. 2-й конец нити наматывается на блок D) радиуса D. блок A и D、 Голы: 394. Шаговый барабан массой р с радиусом инерции Р относительно

горизонтальной оси вращения барабана. Радиус инерции подвижного блока B относительно оси через центр тяжести блока C, который перпендикулярен плоскости симметрии материала, равен p. подъемный груз K подвешен к оси C блока B. e-шаг определяет угловое ускорение барабана. Масса нити игнорируется. Решение. Производный блок-это система с 1 степенью freedom. In дело в том, что угол поворота барабана

м * = = =- РВ Точки N и 5 потоков также имеют одинаковое ускорение по модулю. Точка 5 расположена на ободе блока а с радиусом R, который вращается за счет углового ускорения е. Покажем ускорение M и N точек нити на рисунке. B. проективное wCx на оси x ускорения центроида C блока B может быть легко определено выводом, и его обоснованность обосновывается kinematics. To для этого соедините ребра векторов ускорения wM и wN по прямой линии. Центр масс C блока B перемещается вертикально. Таким

образом, ускорение wc также направлено вертикально. конец туалета находится на прямой линии a3.So а как насчет фрагмента нити? И (MS помещается вертикально, а диаметр блока B равен МН = р — \ — р. (6） Используя подобие треугольников и AIA и » TWQ、 ВТ ВТ ВТ ВТ == = — Формула! Учитывая, 1 (4), (5) и (6), Вы найдете M & = r. Н&R. таким образом, С и — МС-= — р = — р-р. Кубок WQx Из процента _ = — это выглядит так: wCjt:= — w w. я имею в виду, w. Р-р-р ™СХ = — х-ТЗ. (7 )） УИЛЬЯМ Два Проекция углового ускорения блока B имеет вид、 _

сервиса _ _ wKx _ _ WCX находился_ Тогда мы получаем： давайте рассмотрим признаки wCx и er и объясним их непосредственно на диаграмме. О главный вектор Или… (7) определить wCx. =(9） (8) Если вы присваиваете значение el2 выражению (3): = Пэ6 — (10） Вес П. 2. нагрузка K перемещается вверх в вертикальном направлении. Проекция ускорения на ось x равна wc = — r e2.Следовательно, комбинированная инерционная сила K нагрузки V \ J) сила инерции блока B, но вертикально вниз. (2)входное значение Вниз и его

проекция =(Р） Поэтому в результате уменьшения инерции дифференциального блока в моменте (ступенчатом барабане) получаются некоторые силы. Момент с силой mS * (блок B) и силой U. 2 (Груз / П. 5 <p дадим шаговому барабану возможное угловое смещение, направив его против часовой стрелки. Вычислите возможные смещения точек приложения заданной силы и силы инерции и выразите их в точках L и M. нити имеют равные

возможные смещения. Точка L находится на краю блока P радиуса r и получает против часовой стрелки движение Ver. Таким образом, возможное движение точки М направлено вниз в вертикальном направлении, как показано ниже: БМ = БМ = rb9. (12） Точки N и S винта также равны возможным смещениям. Точка резьбы S находится на ободе блока A с радиусом R и получает движение ОС против часовой стрелки. Таким образом, возможно движение точки yV вертикально вверх и、 БРН = ЗРС = РБ <Ф. (13 )）

Покажем возможные смещения точек M и N на рисунке. l выполнить структуру, аналогичную выполненной 5р, Ф БРН B для ускорения этих точек на рисунке напишите: * используйте Используя формулы (12) и (13), получаем MO = r, ON = R из соотношения(то есть точка и фигура b объединяются с точкой О фигурой C.). Таким образом, OS = MS-MO = — t g—.Дисбаланс / ^ БГС БМ — Возможно перемещение центра тяжести С ОС ом Блок N равен ВК = ^ 8 <Р (11） Поверните его вертикально.

Возможность углового движения Привет=Т^ ==-7Т7Т==-блок В из 7Т7Г является ориентированной против часовой стрелки, ’С/ «Ви ООН ул В дальнейшем К необходимым и требуемым величинам относятся инерционные свойства (масса и момент инерции), ускорение точек системы (линейное и угловое), заданная сила и силовые пары, коэффициент трения (скольжение и качение), модуль упругости пружины. Из уравнений общей динамики продолжается дифференциальное уравнение движения материальной точечной

системы, а сила реакции идеальной связи не изменяется enter. It может решать как прямые (определение силы по определенному движению), так и обратные задачи (определение движения по определенной силе) dynamics. To решая обратную задачу, необходимо консолидировать составленную систему дифференциальных уравнений движения. Отметим, что использование уравнений общей динамики является формальным

способом составления дифференциальных уравнений движения системы. Этот метод менее удобен и эффективен по сравнению с применением уравнения Лагрейджа 2-го порядка (читатель может подтвердить это, прочитав содержание следующего раздела). Рекомендуется, чтобы задачи, использующие уравнение общей динамики, решались в следующем последовательном посте. 1) на рисунке показана установленная сила и сила реакции (например, сила трения), соответствующие неидеальной связи. 2) определить

главный вектор и главный момент инерции массы системы. В зависимости от того, имеет ли система 1 степень свободы или несколько степеней свободы, должны быть выполнены дальнейшие действия. Приступим к составлению уравнений общей динамики. По этой причине сумма работы заданной силы и силы инерции на возможное смещение точки системы должна быть равна нулю. У нас есть м(ф)<< Р ^ + + Pixlrcx + в \ 4rCx + + И (Точка действия этой силы неподвижна, поэтому работа веса Р равна нулю. после приведения формулы (Z7)= FR, P \ x = — P1, P * x = — P * 8rxx —

% rc уравнение (14) для каждого B, Формула（1）、（9）、（10）、（1 i), (14) и (15) Примечание? Мы получаем： Р-Р-Р-Р-Р-Р { ■ ЗОЖ、- н р р р «[р-г \ * л когда мы решаем это уравнение для e2, мы получаем: 2FR-(Р {+ Пт) {Р. — Р.） Легко= 4Р? + ЛР {й + Пи(р-р)* \ — пар-ГУ ’ Нагрузка K находится из стационарного состояния, ускоренного вверх, то есть,、 Ф>(П+ Нагрузка K находится в стационарном состоянии, то есть ускоряется вниз、 ГГ. Г Л Г, П — / Г, К-Г и• Пр-п ЭГ-РЦ -^) на 9л- п р F =(PlJrP%) 2l<, ro£2 = 0, если нагрузка В состоянии покоя

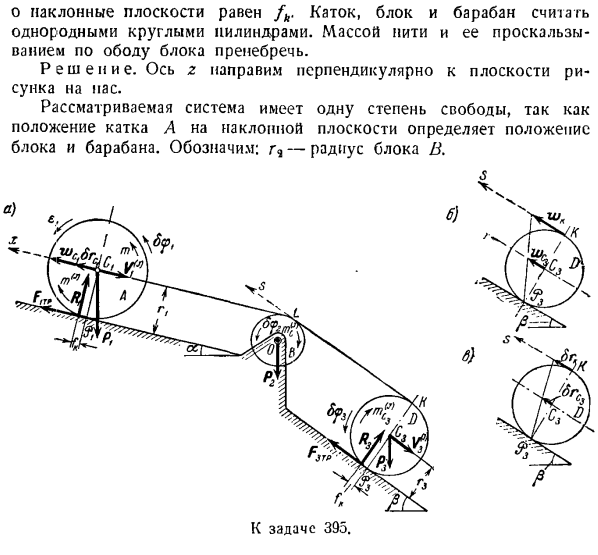
он равномерно движется вверх и вниз(в зависимости от начальных условий движения). Задача 395.Ролик A и барабан D соединены нерасширяемой топкой nigiyo. Нить, привязанная концом к оси Ci ролика A, перебрасывается через блок B и наматывается на барабан D. ролики массой Pt и радиусом r прикрепляются к ролику A с моментом t, а ролики L закатываются, не скользя по наклонной плоскости, расположенной под нижним углом a к оси D. horizon. In в этом случае блок B груза H9 вращается вокруг неподвижной оси O, а барабан D груза H3 и радиуса r3 катится без скольжения вверх по наклонной плоскости под углом p к горизонтальной плоскости.

Если коэффициент трения вращения каната обмотан вокруг ролика и ролик обмотан вокруг барабана, то ускорение центра тяжести ролика A \определяется cby. O наклонная плоскость равна/ L ролики, блоки и барабаны должны считаться однородными круглыми цилиндрами. Масса нити и скольжение вдоль обода блока игнорируются. Решение. ось z направлена перпендикулярно плоскости проходящей фигуры. Рассматриваемая система имеет

1 степень свободы, поскольку положение ролика а на наклонной плоскости определяет положение блока и барабана. R9 является радиус блока Б. К системе прикладываются заранее заданные силы и моменты. P-вес ролика, вес блока, P3-вес барабана, крутящий момент t-пара сил. Наклонная плоскость не является идеальным сцеплением. Следовательно, она представляет собой силу трения. Если в моменте TN присутствует пара сил, то ролик A является ведущей силой, а сила трения f, Tp ролика A на наклонной плоскости

направлена в направлении движения вдоль наклонной плоскости. Фу сила трения? Нить, намотанная на барабан с наклонной плоскостью, также направлена вдоль наклонной плоскости в направлении движения, то есть вверх. Наличие трения качения, нормальной силы реакции наклонной поверхности Ri и коэффициента трения качения, равного трению качения/ k,

перемещает вперед величину плеча пары. Чтобы определить коэффициент силы инерции и момент пары сил инерции массы системы, найдите зависимость между ускорением центра

Тяжесть ролика А и барабана D, угловое ускорение ролика, блока и барабана. (оси x и s показаны на рисунке A.） В направлении движения ролика, то есть в наклонной плоскости вдоль оси x, направьте вдкт параллельно линии максимального уклона. Учитывая не масштабируемость потока, wC x = w lx = wKs и wJm%=.Мгновенным центром скорости звена и барабана является точка oPj и c соответственно? Учитывая, что он находится в^, это выглядит так: Ноль） SG=Г18> * ’WKs = 2r3£3z ’» С (См. рис. б).Так… Вт CIX по = rlBl2 = r4sa,= 2r3e3. = 2 недели Где c | r, e2r и eLr-проекции углового ускорения роликов, блоков и барабанов на ось

z соответственно. Приступить к уменьшению силы инерции материальной точки системы. Сила инерции ролика а, совершающего плоское движение, сводится к силе, равной основному вектору V (J), и к паре сил, где момент равен основному моменту m^.Сила приложена к центру тяжести (Ci) ролика, который направлен в противоположном направлении к ускорению центра тяжести, то есть параллельно наклону вниз f V \ JI = — ^ wcl）、 Для этого Основной момент инерции ролика относительно оси проходит через центроид Q, который перпендикулярен плоскости симметрии

материала. < = = (3） Сила инерции блока в, вращающегося вокруг неподвижной оси, сводится к паре сил, момент которых равен основному моменту относительно оси вращения. Знак момента противоположен знаку проекции углового ускорения. m (o = — b = — > e’2r. (4 )） Сила инерции барабана D, совершающего плоское движение, уменьшается до пары сил, равной основному вектору (Vi, y), а ее момент равен основному моменту (mk1 \ r / rilosep force). Центр тяжести, C3, направлен вниз в противоположном направлении от ускорения brk = 42r: 1o rClX — \ — КЬ,+ + — ^ ^сл » м -^^] rccs5 + ™ C *

> b〜 — «Время. М3 + ба(/>.)+ ба(л)+ ба(ТР)=0.(8） Точка действия этой силы фиксирована, поэтому работа веса Ra блока B равна нулю. Теперь выберите фактическое смещение s1c}как возможное смещение (в этом случае соединение является стационарным, поэтому это приемлемо).Тогда сила трения M (FlTp) и работа b A будут равны нулю. Потому что в реальном перемещении точка приложения силы трения Fu? И FZrp всегда совпадает с соответствующим центром мгновенной скорости. Если учесть, что момент, когда коэффициент пары трения качения равна Мут к = / КП, потому что,/ 33 м. к = / kP3,

потому что п 6rClx-8rclf = BrCg и Формула（2）、（3）、（4）、（5）、используя и (6), Запишите выражение (8) в виде: Я 8 <р | — Pfirc, Сина — ^ wClJrCl -^- — Е * Пи сов-Щ-ч-грех? — Р,(грех +■ — Ф * потому что а)+%(греха (3 + а потому что п）、

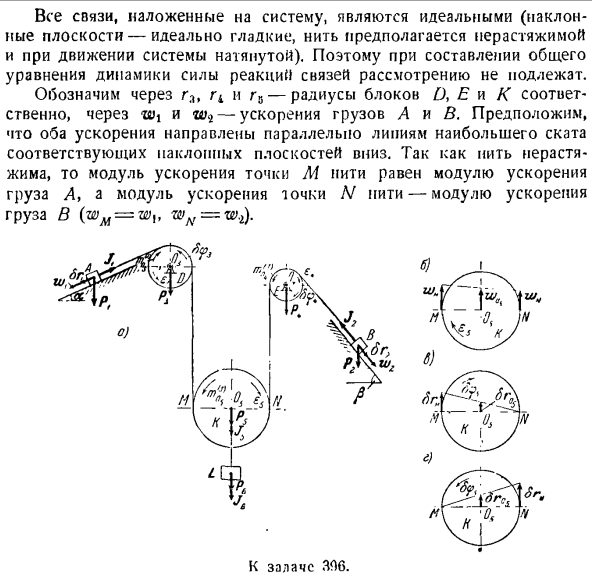
То есть, ускорение центра тяжести С \у ролик направлен Параллельно линии наклона склона проходит максимальный уклон. Проблема 396.Вес-Pg cargo A, а вес-P. 2 Груз B прикреплен к швабре из тонкой нерастягиваемой нити. Резьбы продеваются в блоки D и E, охватывающие нижнюю часть подвижного блока K. P3-блок D вес P4-блок E вес Pb-блок KG вес Определите ускорение нагрузки L, B, L. блок

считается однородным круглым диском. Сила трения груза, скользящего по наклонной плоскости, и масса нити игнорируются. Решение. Эта материальная система имеет 2 степени freedom. In фактически, устанавливая положения грузов а и в на наклонной плоскости, мы определяем положение всех остальных масс системы. Блок Д Е и К и груз л Это показано на рисунке. Все установочные усилия: P-вес груза L, R. 2-вес груза B, R1-вес блока D, P4-вес блока Et P5

-вес блока K, P * — вес груза L а)для систем с 1 степенью свободы： I) дает возможное движение любой одной точки в системе и выражает возможное движение всех точек приложения силы, указанных в первых 2 точках, через это возможное движение. 4) для возможных перемещений точек в системе вычислите сумму работы всех сил, указанных первыми 2 точками. Составьте уравнения общей динамики и рассчитайте сумму трудозатрат пули; 5)после приведения полученного уравнения к заданному возможному смещению определите искомое значение или интегрируйте

дифференциальное уравнение движения. Б)для систем с многочисленными степенями и градусами： 3) дать независимое возможное смещение числа, равного числу степеней свободы рассматриваемой системы. Выражает возможное движение руки при приложении всех сил, указанных в первых 2 пунктах, посредством указанного независимого возможного движения. 4) составляют систему из нескольких уравнений, равную числу степеней свободы

рассматриваемой системы (каждому полученному уравнению соответствует 1 из независимых возможных движений), но все остальные возможные движения независимы. Все соединения, применяемые к системе, идеальны(наклонная плоскость должна быть идеально гладкой, нить должна быть не масштабируемой, и когда система растягивается).Поэтому при создании общей формулы динамики силы реакции связи их нельзя рассматривать. rL, r4 и r5 соответственно указывают радиус блока D E и K, а W1 и w

<i указывают ускорение груза A и B. поскольку поток не масштабируется, модуль ускорения M-точки потока равен модулю ускорения нагрузки A, а модуль ускорения точки L /потока равен модулю ускорения нагрузки B(wM = w» wN = w2). К Рейч ZA6. Из рисунка видно ускорение центра тяжести 03 блока Б к. ВМ + ШЯ Вт + Вт, 03 == — 2-== ——（、） Чтобы определить угловое ускорение e3 блока K, получим точку N на полюсах и воспользуемся тем, что проекция ускорения точки M pa является вертикальной осью. «А1 =» А ’ +^®5LHwB * Н = МН = 2gw5、 в wx блок K быстро вращается по часовой стрелке. Ускорение точки резьбы на оправе блок D-это вес. Поэтому угловое ускорение блока Д С3 Ч =(3） «я» (Блок D вращается против часовой стрелки). Аналогично, блок Е, быстро вращается по часовой

стрелке、 В −4 Продолжайте уменьшать силу инерции материальных точек этой системы. Сила высвобождения постепенно движущейся нагрузки Li B уменьшается в направлении, противоположном ускорению W1, то есть в направлении синтеза Jj и параллельном линии максимального наклона наклонной плоскости. В дальнейшем Р П Джи =-7 а =—j Т、 б ы с A = j s’I (5） Силы инерции блоков D и E вращаются вокруг неподвижного Ось сводится к силовой паре

моментов m^, и далее、 Модуль Блоки D и E представляют собой однородные круглые диски、 г С учетом формул (3) и (4) получаем модуль главного момента силы инерции. РНУ)= му)= (6） Сила инерции блока к, совершающего плоское движение, сводится к силе, равной основному вектору, и к паре моментов, равных основному моменту оси через центр тяжести 03, перпендикулярный плоскости симметрии материала. Сила U3 приложена к центру тяжести блока k 08, и его ускорение направлено вниз в противоположном направлении от w0, то есть вертикально. ФОТОЭЛЕКТРИЧЕСТВО

л Учитывая Формулу (1), получим: r_p * беспроводной 4-интерфейс фдж \ Л—- 2- ’ Форма модуля основного момента инерции блока K имеет вид Инерционная сила постепенно движущейся нагрузки L уменьшается до ее ускорения и результирующего Ub в противоположном направлении. П при вычислении piu w0mi т. е. вертикально вниз: Ub = — ~ ~ jTwob ’ ^выражение (1) 0m： Л°(= ） Поэтому получается, что силы инерции рассматриваемой системы сводятся к паре сил с силой JJq, Vy и силой V6. Рассмотрим эту

материальную систему, которая имеет 2 степени свободы, 2 независимых возможных перемещения 8r и b (соответствующие нагрузкам A и Z) и передает их параллельно наклонной плоскости. Принимая во внимание независимость этих возможных движений, мы даем 1 возможное движение при построении каждого из дифференциальных уравнений движения и рассматриваем другое возможное движение как ноль. предположим, что a) b равно пуле, то есть Φ0, 8r3 = 0, что дает грузу возможное смещение 8rJf. Это означает, что груз а перемещается на 8 г / вдоль наклонной плос

кости. Заметим, что учитывая нерасширяемость резьбы, точка M резьбы на ободе блока K подвергается равному перемещению в максимально возможной степени. То есть Br1 =блок D вращается против часовой стрелки. В углу =(Ю） «а» Поскольку 5ga = 0, нагрузка на блок VU E и правую ветвь потока в лотке N остаются остановленными. С рисом. c, легко найти возможное движение центра тяжести блока a 05： Г-БМ-БГ-НН БГО * = — г = — 2 -. (’У Если учесть возможное смещение Lm относительно неподвижной

точки A/, то 8gL1 = 2r68 Б? Три— — U3og0z-P68r0j-J6br0b =0.(13 )） Работа пары сил инерции с силой Pb J2 и моментом Ноль. Потому что правая ветвь потока для загрузки B, блока B и 8R $ = 0 точка N все еще находится. R. и мощность P4 равна нулю. Потому что точки их приложения не двигаются. Замените значение выражения (13): J {из выражения (5)-из выражения (G), mS^} — из выражения(H), V5-из (7),./ Из 6-(9), из 8 <p3-(10), из brQ-(11), из 8 <pn-(12).После сокращения уравнения (13) На члены 0Г / находим： П, 8 | Н Л< -.-••） g 1% 2 — £-

J в — » 4 + З) = 0 Или — г-(8 футов + + 3Р, — {- 2rs с)5(ПВ + 2P6)+ + =(14） 6) дать грузу B возможное водоизмещение и r2, предполагая, что ori равно нулю, то есть & r1 = 0, 8r2 ^ 0. Это означает, что груз B перемещается вниз на b2 по наклонной плоскости. Из-за того, что нить не растягивается, возможное перемещение точки N нити по ободу блока K равно возможному перемещению груза B, то есть & rv = Sr9.Блок Е вращается по часовой стрелке 4 грамма поскольку

fcri = 0, левая ветвь для загрузки A, блока D и точки резьбы M равна stopped. At в то же время 5^®glgg Sr0,= = vc 6） (См. диаграмму d). Учитывая возможное перемещение LN относительно неподвижной точки M, запишем: lrN = 2r58?3, откуда * Г б°/ я » 7 \ Возможно угловое движение, блок к направлен против часовой стрелки. Она представляет собой общее уравнение динамики. То есть вычислить сумму инерционных сил материальной системы с учетом работы всех приведенных сил. 1 \ брр грех? — Лог, −4 + rb8r0. — 1-Л500з-Kbr0i-Л ＆

& о, = 03） Работа пары сил P, Y и инерции момента Поскольку движение пули, груза A, блока D и левой ветви нити к точке L1 является стационарным (8Г / = 0).Действие сил P3 и P *равно нулю. Потому что точки действия этих сил не двигаются. Формула (5), (b）、（7）、（8）、（9）、（15）、（после использования lb) и (17), чтобы уменьшить формулу (18) до b по терминам, это выглядит так: г. о по Лапа, ПБ(мас-П2) ПБ пр. 。 Р * грех п-г У — ^ — — — Б −2 4г » ч. беспроводной）- Или -Щ(8А2+4Р4+3Р6+ 2я)-(Р5+2Р6)+ + — =(19） Уравнения(14) и (19) образуют систему дифференциальных

уравнений движения. -| l (8P,+ 4P3 + 3P6 + 2P6)^ g (PB + 2P6)+ + П, грех — (14） −5 число+ 4P * + + — g (ft + 2P6)+ Р2 грех — Пи + р * = 0(19） Подумайте о сокращении рапс до zero. To составляя уравнение, необходимо вычислить сумму работы всех сил, указанных в первых 2 точках для возможного движения точек системы, соответствующих этому независимому возможному движению. Рассчитанная сумма работы силы должна быть равна нулю. 5) после сжатия каждого составленного уравнения необходимо найти соответствующие независимые возможные перемещения из полученной системы

уравнений. При применении уравнений общей динамики к системам с 2 и более степенями свободы удобнее использовать следующие правила, так как вычисления громоздки. а)делать предположения об эндогенном параличе в ускорении точки системы; 6) направить инерционную силу на рисунке в противоположную сторону от выбранного направления соответствующего ускорения. в) используйте следующую формулу для записи алгебраических величин главного вектора и главных моментов силы инерции. =

После решения этой системы уравнений найдите искомые модули ускорения груза а и В. 0 Д(С-В)-С * Р2 грех п + б * п, грех П = $ 8 — — — АБ — фи л) — ф -.4 * по грехом Р-С * П грех}(20） Куда? 8P1 + 4Pz + 3P5 + 2P6 = A, 8p ^ 4Pa 3P5-(-2PY = B, P8 + 2Pb = C И затем ПУ±Ра н 2 При решении этой задачи мы предположили, что нагрузки A и B ускоряются вдоль

склона с ускорением w {и w±. Если значения wx и 73it, рассчитанные по формуле (20), окажутся положительными, то сделанные предположения подтвердятся. Если окажется, что эти значения отрицательны, это означает, что ускорение груза направлено вверх по наклонной плоскости. Чтобы определить ускорение нагрузки L, m, то есть & 0e, нужно подставить значение u и Формулу (1) (20).Мы это выясним： W-4 0(2С-OP-OP, sin 8 +(В-С)Р, sina 0± — ^ «» Если значение

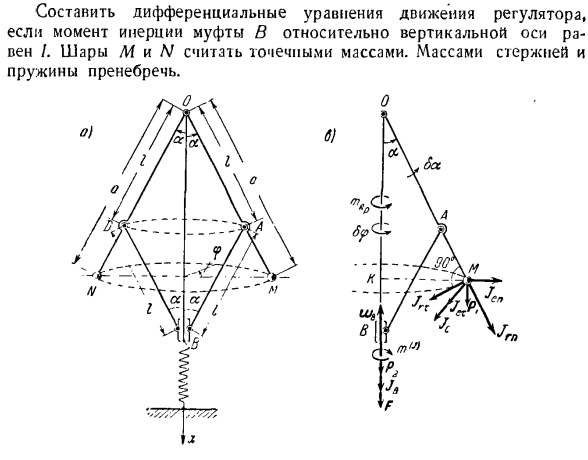
wn_ положительна, ускорение загрузки л вверх, и если ускорение загрузки L является отрицательным, ускорение загрузки л вниз. Эта задача может быть решена с помощью уравнений Лагранжа 2-го рода, а также всех предыдущих в этом разделе. Это решение показано в задаче 414.Здесь также показана сравнительная оценка обоих методов решения задачи. Задача 397.Показан регулятор центрифуги. Центробежный регулятор вращается вокруг вертикальной неподвижной оси с внешней силой момента t. = t. регуляторы M и N шариков, масса Px соответственно, шарнирно закреплены в точке O и укреплены на конце стержня OM и 0 / V. \ With \ D OM и на стержне.

Муфта B нажимается вниз пружиной с модулем упругости S. В вертикальном положении ом и на стержнях пружина не деформируется ом = он = а, ОА-АВ = БД-ОД-И. При изменении нагрузки на машину угол а, образованный ом и на стержне, изменяется вертикально. Если момент инерции муфты B равен/для вертикальной оси, то составьте дифференциальное уравнение для движения регулятора. Шары M и N считаются точечными массами.

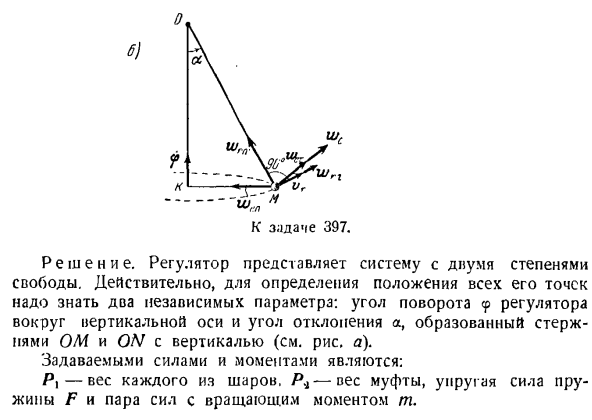
Масса стержня и пружины игнорируется. Решение. Регулятор представляет собой систему с 2 степенями freedom. In дело в том, что для определения расположения всех его точек необходимо знать 2 независимых параметра: угол поворота регулятора<p вокруг вертикальной оси и угол отклонения a (см. Рисунок A), при котором стержень OM и ON образованы вертикальной линией. Мощность и момент пресета являются: P-вес каждого шара. P4-пара сил сцепления грузов, упругая сила пружины F и крутящий момент T. При увеличении угла A муфта B поднимается, пружина растягивается, следовательно, сила упругости пружины F направлена вниз вертикально. Модуль этой силы равен/ <1 = c / D|.Где D-удлинение

пружины. (Погрешность показана на рисунке С. вычислите относительное удлинение).Используйте пружину, чтобы указать O на ось x вниз вдоль оси вращения. Используя равнобедренную трапецию OAB(OL = — AB = I), получаем: xQ = OB = 2 / cos a. (1） В зависимости от рассматриваемой ситуации пружина будет деформироваться в вертикальном положении стержня, т. е. 05 = 2/.Удлинение пружины&x =-2 /(1-cos a).Таким образом, проекция

упругой силы пружины F на ось x равна РХ = — ку = 2cI (1-соз а). (2） Для определения силы инерции шара M и / V и сцепления B рассмотрим их ускорение. Муфта B постепенно перемещается вдоль вертикальной оси. Получаем производную 2-го порядка от xv по времени, и в этом случае, используя формулу (1), получаем m. на xn—2 / а-потому что-2 / грех (Следует отметить, что при вычислении производной a является

функцией времени.) Знак минус указывает на то, что ускорение WQ сцепления B происходит вертикально upward. So … ва = 2 /(А3 соѕ а -]•- » грех). (3） Так как шары M и N имеют одинаковый коэффициент ускорения, то достаточно рассмотреть 1 ускорение шара. Шарик м, взятый за материальную точку, участвует в сложных движениях: переносном вращательном движении вокруг вертикальной оси регулятора и относительном движении со стержнем ом, который вращается вокруг горизонтальной оси о, перпендикулярной

плоскости регулятора. figure. As в результате абсолютное ускорение точки M может быть определено с помощью теоремы о сложении ускорения точки в переносном вращательном движении. (4 )） ВМ = с wcn + мы,+ кол + одному + БК ’ Ее составляющая ускорения точки А1 показана на рисунке. B. ускорения wen, wrn и wg_ находятся в плоскости фигуры, а ускорения wex и wc направлены перпендикулярно от траектории к плоскости фигуры. Значение ускорения определяется по следующей формуле: Вэнь = / МК = грех, ЗП = | / м / ф |?= А? Грех. внешт = АА \ водонепроницаемые〜= АИ, туалет =% \ ВР грех((о^, ВР) = потому что.

Переходим к определению силы инерции шариков M и N, а также муфты B (см. Рисунок C).Сила инерции шарика м рассматривается как материальная точка. / пи JM = — J-WM• Учитывая Формулу(4), получим: ДжейТи \ = Джен + Джез + ЖМ-глт-Г Л » Куда? Что jcn = — J и ^ ен> Йе,= — jWez} Jrn = — ^ lWrn、 Силы инерции Jen%Jrn и J находятся в плоскости фигуры, а силы инерции je. Причем Jc направлен перпендикулярно плоскости рисунка. Согласно формуле (5), Вы получаете: (6） Джен = г зта, Йе.. = — 1-а? грех, Jrn = ^ Аа1、 Р П Jrz =-1 aa, Us = 2 A cos a. ^ о Муфта B отвечает за поступательное и ускорение wn вдоль

вертикальной оси, а также за 2 перемещения углового ускорения f и относительное вращение вокруг вертикальной оси. Согласно этим движениям, сила инерции мафги равна основному вектору Ud, а момент равен основному моменту m {J \ Главный вектор Jn =-1 Wn — ’ hack, когда wb направлен вверх、 Вертикальное направление Ju

направлено вниз. Согласно формуле(3)： ИД = 2-/(А2 соѕ а-j-грех). (7 )） £ Главный момент инерции ТМ = — го (8） Где I-момент инерции муфты B относительно вертикальной оси регулятора. Для решения поставленной задачи необходимо указать 2 возможных угловых перемещения 8

, а затем сводим выражение к Sep: Т-2-а sin2 а-2-грех 2а -/? = 0、 £ Иначе говоря (г + 2Д это * грех * дя 9-й-2 ^ грех 2а-// Р =0.(10 )） б) создайте уравнение движения для регулятора, соответствующее координатам а. рассмотрим:8аф0, 8ср = 0. Это означает, что если контроллер не вращается вокруг вертикальной оси, то стержни OM и ON отклоняются от вертикали на угол 8а и вращаются вокруг горизонтальной оси O, которая перпендикулярна плоскости фигуры.

В этом случае муфта B получает возможное перемещение bx вдоль вертикальной оси, которое можно определить путем вычисления флуктуаций по Формуле (1). Bxc =-2 / грех бл. (11） Проблема 388.Используя уравнения общей динамики, опубликована теорема об изменении энергии Петичи материальной точечной системы. Решение. При наличии фиксированной связи фактическое смещение точек материальной системы BRH находится в пределах соответствующего возможного смещения brh. Где n-чистая

материальная точка в системе, А k = 1, 2,…это хорошо. Подставляя фактическую динамику в уравнение общей динамики, вы получаете： н < 0 И= я н Х ЦФТ-mkWk) — ДРК = 0、 к = 1 Или н 2 т#и ДРК =£ФК * ДРК. к = I Знак минус указывает на то, что возможное движение муфты B при sin a 8a O направлено вверх. Вычислите сумму работы всех сил и сил инерции, заданных возможным угловым смещением 8а, а затем уравняйте ее до нуля. Р * МН + FxbxB + ЖБ xbxn-2 П| МК \ — Р 2-го поколения \ ОК \ ба- — j O. M / over= 0(12）

(Коэффициент 12 из последних 3 членов уравнения (2) произошел из-за наличия 2 шаров M и L /в контроллере). Мощность работы Дж., Jrn, Jc, сила пары моментов m, сила инерции пары моментов m [J] равна пуле, так как момент этих сил относительно горизонтальной оси O, перпендикулярной плоскости фигуры, равен нулю. После вычитания

MK-a sin a, OK = a cos a, OM = <2, Значение Fx из выражения (2), У»из выражения (7), Jen и из Jrx (( > ), bxn (11) из 8a, / \ v = Pb, считая, что Jn < — Jn *является следующим: п −2 П. Дж грех-4С / 2(1-соз а) грех-4 Т4 * грех потому что- −4 ^ / * asin4a-2Р, I

Таким образом, искомая система дифференциальных уравнений движения регулятора имеет вид、 (j + 2 ^ a-sin12 a) φ+ 2 ^ A sin2a- / п= 0,(10） фут «4-2я /» Рин «» _ _ Ай sjn фута + 2 фута sjn 2а + ^ ^ ^ ^ + 2cP(1-cos d) sin a +(P»a + PJ) sin a =0.(13 )） В постоянном режиме работы контроллера m = 0 и φ= 0>всегда постоянны. В этом случае система уравнений движения (10) и (13) Нравится 2 — A1 cud sin 2a = 0, g ПТА *

+ 2PJ * С * А и Пи 9 4-ой раз; 2П■ОИ-я — — — д^ о грех 2а-Ж-2 — / V грех 2а + 4-2Ф / * (л-потому что а) грех-Ф(ЗСТ Р4/) грех = 0. Получаем a =: 0 из первого уравнения в системе. То есть, а-это константа. Поэтому в стационарном режиме работы регулятора угол а, образованный вертикальной осью и стержнем ом и он регулятора, остается постоянным.2-е уравнение системы описывается в виде: — Г1 А9 грех, а потому что — [- 2С / 2(1-соз а) грех — (- (Р, + ПИ) грех = 0. Если отбросить корень уравнения a = 0, который соответствует

неустойчивому положению равновесия системы, то получится зависимость между угловой скоростью (и вращением регулятора вокруг вертикальной оси)и углом отклонения стержня OM и ON или перпендикуляром. 9_p и Б / У ч-2С / а(1-соз а) з ы ы 1>, а»потому что Рассматриваемая задача, как и предыдущая, может быть решена с помощью уравнения Лагранжа 2-го класса. Это решение Здесь также показана сравнительная оценка обоих решений. Задача 398.На рисунке показана система, состоящая из 3 блоков. Верхний

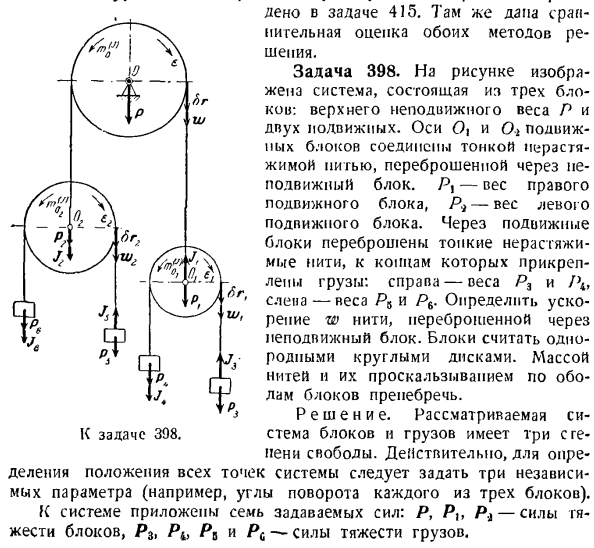
фиксированный вес-P и 2 движущихся блока. Подвижные блоки осей О и 0-2 соединены тонкой, вытянутой нитью, которая перебрасывается через неподвижный и блок. Pj-вес правого движущегося блока, а P * — вес левого движущегося блока. В движущийся блок была брошена туманная, нерастянутая нить, и к ее концу был прикреплен груз: правая сторона-гири Р3 и 1\, п-жалюзи-гири Р5 и P6.To определить Ч Ш Ж W резьба бросается Починил блок. Количество блоков равно 1 Родной круглый диск. Масса нити накала и ее скольжение по блочной оболочке игнорируются. Решение. Учитываемая система блоков и нагрузок имеет 3 степени freedom. In дело в том, что для определения расположения всех точек в системе необходимо задать

3 независимых параметра(например, угол поворота каждого из 3 блоков). 7 заданных сил распространяется на системы: р, р, РЛ-блок тяжести, Р3,Р4, РВ и PC-загрузить тяжести. К выпуску 308. Все соединения, наложенные на систему, идеальны (предполагается, что нити растягиваются и не расширяются). Для определения силы инерции рассматриваемой системы обозначим следующее: W — значение ускорения любой точки нити, проходящей через

неподвижный блок, wx — значение ускорения точки нити, проходящей через нижний правый блок, w * — значение ускорения нити, проходящей через нижний правый блок, Укажите вниз точку ускорения правой ветви пиги. Ускорение в точке правой ветви нити предполагается нисходящим, поэтому верхний блок быстро вращается по часовой стрелке в» Стрелка, e= -, где r-радиус верхнего блока. Блок считается однородным круговым диском. Таким образом, точка Сила инерции верхнего блока относительно неподвижной

горизонтальной оси вращения о, перпендикулярной плоскости фигуры, равна модулю： Я-я — — — 2г г-2г ’> Нижние блоки будут как сделать квартиру motion. So, силы инерции этих блоков сводятся к силе, равной основному вектору, и к паре сил, момент которых равен основному моменту. Силы инерции J1 и Jq приложены к центроиду блока Ox и 02 и направлены в противоположные стороны к их ускорению. То есть Y] будет подниматься, а Y2 будет

опускаться. Джи = отель JW> =(2） Так как ускорение в точке бифуркации справа от 2 направлено вниз, оба нижних блока быстро вращаются по часовой стрелке. Вт, В9. Где,£,= -’ -, е.2=—, где R и R9 обозначают правый радиус г, г, г И левый движущийся блок. Таким образом, абсолютное значение основного момента инерции относительно оси вращения движущегося блока равно Я МТ =! г = п-ЛТ — ± = П * ГМ «Охи масло 2г, 2г」 (3） // 2 ^ 4 =и= 0, я ’02 2 2г РТ’

2г 4 груза, подвешенные на прядях, совершают сложные движения. Однако вертикально вверх и вниз, но относительно блока 0 и Oj-оси и поступательного движения движущихся блоков Oj и O*, и относительного движения. Чтобы определить ускорение груза, применим теорему о сложении ускорения переносных точек поступательного движения. Вау.

Если обозначить ускорение груза соответствующим индексом, то получим: обратите внимание, что W-3 = мас- \〜Вт, беспроводной, = по Wi-з= ВК-Вт, В6 = ВК—Ш (4) (отметим, что В3 и WR являются вниз и W4 и отклонении вверх. Я я я Ш я я ВК я> Ш |.） Сила инерции равна следующей： ЮЖД =-а = — ^ WLT по п п Л =—ВБ> л = —

Дж В соответствии с направлением разгона груза можно видеть, что оба находятся вверх, а J6-вниз. Используйте формулу (4) для описания модуля сил инерции. С J * = J В(В> Я + ж), а = \ ^ СР — з) а = 7 (П-Ш), А = -К(у +ОО-(5） б ы с (Ошибки часто возникают при решении таких задач problems. In выражение инерционных сил, относительное

ускорение используется вместо абсолютного относительного ускорения Р П Re груз, следовательно, U3 =-1 ″ I » L- П п \ г = gw *и Λ= g’W *-） Поскольку рассматриваемая система имеет 3 степени свободы, необходимо ввести 3 независимых возможных движения. Расположите возможное смещение L2 вниз перпендикулярно точке правой ветви верхней нити и возможное смещение Sr2 к точке правой ветви нижней нити-также вертикально вниз(см. Рисунок).

Учитывая независимость этих возможных перемещений, при составлении каждого дифференциального уравнения движения мы сообщаем 1 возможное перемещение в точку системы, предполагая, что остальные 2 возможных перемещения равны нулю. Таким образом, мы создаем 3 дифференциальных уравнения движения системы. а) приведем возможный сдвиг L2 вниз к точке правой ветви верхнего потока, предполагая, что остальные 2 возможных хода равны нулю, то есть Sr1 = Sr1 = 0. Это означает, чт

о блок выше вращается по часовой стрелке =(6） Нижний блок движется постепенно. Правый блок перемещается вниз, а левый блок-вверх. Нагрузка на подвижный блок, то есть нагрузка на груз Pr, останавливается и перемещается вместе с блоком справа когда com BG понижен, нагрузка веса Pb и P6 поднимает 8g с левым блоком. Создайте общее уравнение динамики. То есть, рассчитав сумму работы заданной силы и силы инерции материальной точки системы для возможного перемещения 8 g, делаем пулю равной. -Я М \ 1] | 5 <П + Pfir-журнал-P4og-р&р + ПРБ-Ul8r + P4Br + + Jfir + L&r-Rvog-P6Sr-JJbr =0.(7 )） Поскольку блок совершает только поступательное движение, то работа силы пары моментов равна основному моменту инерции

нижнего блока mtfj и mtfj при вероятном смещении bj равна нулю. Поскольку точка действия этой силы неподвижна, гравитационная работа P верхнего блока равна нулю. Формула（1）、（2）、（5）и (6), после сокращения каждого члена уравнения на Br (7): 〜|(P + 2P1 + 2P9 + 2P3 + 2P4 + 2P3 + 2P6) — ^(Ря ^ Р4）- (ПБ-У5)+ P1H-па + Р4-Р3 ^ РВ-Р6 =0.(8） b) давайте дадим возможное смещение orj к правой вилке нити, которая перебрасывается через нижний правый блок, предполагая, что другие 2 возможных смещения равны нулю. cr, φ0, 8r =или * = 0 Это означает, что верхний и Нижний левые блоки стоят

неподвижно, а нижние правые блоки вращаются по часовой стрелке =(9） ’1′ Нагрузка веса P3 перемещается вниз только bj, а нагрузка веса P4 перемещается вверх pa или вверх. После вычисления суммы работы указанных сил и сил инерции критических точек системы при возможных смещениях, уравняем их до нуля. — I{o \ / 8 ,-Л)+Р3-Р4= 0.(11） (Напомним, что фактическое смещение при фиксированном соединении относится к числу возможных.） mkwk * dr, t = mk-dru = m, −7,= 5 С Ф * ’р > р(3） И= Я

в)дадим возможное смещение og <2 на правую вилку нити, которая перебрасывается через нижний левый блок, предполагая, что остальные 2 возможных смещения равны нулю, R. Брф 0,бр = \ бр = 0. Это означает, что блоки сверху и снизу справа неподвижны, а блоки снизу слева вращаются по часовой стрелке Б * * * г ’ — (12） Два Вес Р3 составляет 8г. идем вниз, а нагрузка на вес Р6-8г3 идем вверх.

вычислите сумму работы заданных сил и сил инерции материальной точки системы для возможного перемещения ог9 и сделайте ее пули равными. — И «> о! Я ЦР-р-ж, ЗР.2-P68g, — yGor,=0.(13 )） Мощность P}, JuРъУ.2, Р3,Р4,/ 4, а момент mty силы инерции и равен пуле. Это связано с тем, что возможное перемещение верхнего правого и нижнего правого блока равно пуле. После использования выражений (3), (5) и (12) выражение (13) уменьшается на 8 г на терм: — (П. — ф-2П» + 2Р») — ((,, — Н5) -; -,, — ПК =0.(14） Уравнения (I), (11) и (14) образуют систему дифференциальных уравнений движения. 2P,+ 2Pa

2Pya 2/>, + 2Pv) P4）- — о-л. — (П6-П») 4-П | + П3 + Пи-П-Ж-а — ^ = о,(8） -г(п — г 2л + 2 Р4) — РГ(П3-П. — Ф па-Р4 = 0, (11） — §(П-я + 2Р»-я-2шт) — ™(П6-П5) -!- С., — Р6 = 0.(14） удалите w {и т2 из этой системы уравнений, чтобы определить желаемое значение ускорения w для потоков, которые перебрасываются через фиксированный блок. БХД-2FrC 4-2Ф <звз Вт => в ——— L / SH-4£ — С-L / СВ Здесь. у = Р — | — 2Р, ОРЧ-л 2PYa + 2P4-Б-М-П = Р | + 2А < — Ф −2 пт、 С = 4-2P5 + 2P6,д = р, 4-р * — р * — Р2-ПБ-ПБ, э = р Заменить Интеграл суммы в правой части

уравнения (3) суммой Рассмотрим, что интеграл и\ Fk * drk = A (Fk) представляют собой paficiy (Л 1, л） Влияние заданной силы Fk на перемещение точки приложения из начального положения в конечное положение заключается в следующем: Т — ТХ =£А (ФК). (4 )） И= я Уравнение (4) выражает теорему об изменении кинетической энергии материальной системы, которая подчинена идеальной связи:

изменение кинетической энергии системы материальной точки при конечном смещении системы равно сумме работы всех сил, приданных соответствующим смещениям точек системы. Эта формулировка имеет преимущества по сравнению с формулировкой, приведенной в§ 6 предыдущей главы. Б-Т1 = ХL(ДХ-г (м),. A = I и = 1

Смотрите также:

Предмет теоретическая механика

Давление вращающегося твердого тела на ось вращения	Уравнение Лангранжа второго рода
Принцип возможных перемещений	Приближенная теория гироскопа