Общая транспортная задача

Общая транспортная задача

• Общие транспортные проблемы Транспортная задача формулируется следующим образом: Есть много производственных (отгрузочных) пунктов одинакового качества Продукт или обменный продукт и η товар Расход (пункт назначения). Известный объем производства (инвентарь).

• Конкретная начальная точка и точка спроса (обязательно) Продукты в каждой точке потребления. Кроме того, а, -, б \ Мера в том же количестве (тонна, шт, вагон) И т.д.). Транспортные расходы также известны. БЦ для перевозки грузовых единиц из (стоимости) пунктов я отправлюсь к месту назначения. Нажмите здесь, чтобы узнать стоимость доставки Условное понятие.

В разных ролях в своих ролях Во многих случаях отображаются тарифы, расстояние, время и т. Д. Людмила Фирмаль

Задача состоит в том, чтобы создать план транспортировки Соответствует минимальной общей стоимости перевозки И это будет гарантировать удовлетворение спроса на все товары * Все потребляется при полной реализации этого продукта Производственная точка. 90 Построить математическую модель транспортной задачи.

Введение неизвестного Xi (i = 1, 2, …, m \ / = 1,2, …, n) 9 Указывает планируемый объем трафика между каждой точкой Каждая точка производства и потребления. Вот так Решение транспортных проблем найдет план Транспорт X = (X \ и * 12, …-, ХЦ * …. * # n / i) = (* f /) i = 1,2 т, МИНИМИ # = 1,2 Общая стоимость перевозки т н ζ-ΣΣ «** ι, (ΐ) Под ограничениями со следующим значением: 1.

Весь продукт от каждой точки производства Полностью экспортируется в точку потребления. Это требование Математически написано как: η ΣЩ = G * * «= 1,2» …> ή. (2) / = я 2. Спрос на каждую точку потребления конкретного продукта Должен быть полностью удовлетворен. Эти условия записываются. Уравнение формы м Σ * ί / = * /. / = 1. 2 тонны (3) 3. Объем трафика должен быть неотрицательным: xc> 0ί = 1, 2, …, м; / = 1, 2, …, м (4).

В дальнейшем вся информация по транспортным вопросам (1) — (4) Полезно суммировать так называемую таблицу транспортных задач. (См. Таблицу 1). Уравнения (2) и (3) получены из следующих строк, соответственно: И столбцы в таблице транспортных задач. Математическая модель транспортной задачи (1) — (4) Это называется закрытым.

Построен на предположениях Общий объем производства этого продукта (Σ ° «) Должно быть равно общему спросу (в пределах Σ ^ / 1)> t · e · м н Σβ / = Σ * / ・ (5) тсал / 5 = 31 Последнее равенство является требованием в то же время Возможность решения транспортных проблем. Это доказывает теорему 1. Замечания.

Задача линейного программирования называется Если у нее есть лучшее решение, оно может быть решено. Теорема 1. О разрешимости транспортных задач Состояние баланса необходимо и достаточно Я Производство и потребление, т.е. Σu = Σfy- (5) Доказательство необходимости.

Подводя итог Все уравнения (2) по очереди, и — (3): tητηητηη ΣΣχιι = ΣodΣΣxc = Σfy- fe = l / = 1 v = 1 / = ίί * = 1 / α = 1 Левая часть результирующего уравнения четко Если есть совпадение, * и его правая часть равны. tη Σαί = Σbh ί = 1 / -1 Доказательство достаточности для условия ‘5. Для доказательства Теоремы достаточно, чтобы создать хотя бы один транспортный план *. с того времени.

• Привет ΣЩ = Σbi = и число xq = -J- i = 1,2, …, m \ j = 1,2, … / i # Χ = ι / = »ι * Приемлемые решения транспортных проблем иногда называют Lancers Транспорт. 92 Создайте план транспортировки для задачи (1) — (4). Конечно, из Неотрицательное (в смысле) a, •, bf и d означает xt> 0. Кроме того, значение выбранной переменной xif Легко убедиться, что соотношение (2), (3), xc выполнено.

Другие ограничения задачи: L ηη V VflA? Λ Ш1 = ц = = Αι- = = Ci ‘- j— = e .. i = 1 тн; / = ι ・, = ■ d В Σγβ.ί>. «* xt = £ 1-y = b, ‘- = j- = ft /, / = 1, …, n. Поэтому набор возможных решений транспортной задачи L * Это не пусто. Также указывает, что L ограничен Много На самом деле значение переменной xc.

Неравенство 0 Людмила Фирмаль

Много с Очевидно, что целевая функция задач (1) — (4) является непрерывной, Затем, с ограниченным набором L, он достигает своего нижнего предела Facet. То есть предусмотрены для транспортных задач (5) Существует оптимальное решение. Транспортные задачи, как и другие задачи, Проблемы линейного программирования не всегда могут быть решены.

Транспортные задачи (1) — (4) являются линейными задачами Программирование записано в штатном фоцме. У нее есть m + n основных условий-ограничений и mn-переменных. 1. Векторный формат транспортных задач. шоу Вектор, координаты которого состоят из коэффициентов через Aif Для переменной xc в ограничениях (2) и (3) -транспорт Задача.

Потому что переменная хс включена в коэффициент плюс Единица системы i-го уравнения (2) и только системы / уравнения (3) Формат векторной последовательности переменного тока: Ac = (0, …, 0, 1, 0, …, 0, 1, 0 0). .-1 — и т + / ч Полные координаты вектора Ak равны m + n. Из них ιth и m + Равно 1, а остальное равно нулю.

Представляя вектор Столбцы (2), (3) соответствующей части условия Ao = (a \ 9 »・ ・ ・ ・ mm» b \ 9 & 2t —f bn). Этот вектор часто называют вектором. Потребление продукции. Кроме того, мы вводим вектор строки, состоящий из: Неизвестный коэффициент целевой функции (1): С введенной нотацией вы можете переписать математику Модель для транспортных задач вида ζ = СХ- * мин. , (6) tη ΣΣMe = Lo; (7) χ> ο. <8) 2.

Зависимость от основных условий транспортных проблем. Там Транспортная задача (1) — (4) может быть решена Баланс между производством и потреблением (5) Указывает на наличие с ней отношений Пределы (2) и (3). Теорема 2 Первая формулировка. Ранг матрицы ограничений Транспортная проблема — это m + n — 1. Вторая формулировка.

Количество условий линейной независимости Транспортная проблема m + n — 1. Доказательство. Очевидно, что обе формулировки Теорема 2 эквивалентна. Для доказательства, Найден набор значений xih, которые удовлетворяют всем Ограничения (2), (3), кроме первого, например. Покажи это Тогда вы должны удовлетворить первое уравнение.

Написать Очевидные отношения с левой стороны слева Первое уравнение ηtηtη Σ * ι / = ΣΣщ-ΣΣχα * (9) / «1 т = 1 / = * 1 В — 2 /» = 1 Поскольку xij удовлетворяет формуле, показанной в (2), Я (3) Σxi = o.i (i = 2, …, m) и 2 xi = 6 / (/ = 1 »2, …, / i), Учитывая это равенство, (9) принимает следующий вид: ηηt tηηt Σ * ι / = ΣΣ * ίΐ — ΣΣ * = = Σ * ί — Σ- , = 1 / = W = 1 t = 2 / «= l / = 1ί = 2 mηηm.

Однако, потому что Σat = Σ & / ・ TOΣfc / -Σβι = fli. c «.l,» 1 f = l t — 2 η В результате Σ * 1 / = H, то есть первое уравнение / — » Украдет выбранное значение. Следовательно, в системах (2) и (3) m + n-1 или менее xc — линейное независимое уравнение. Проверьте также Другие уравнения (2) и (3) в системе Оставшийся результат.

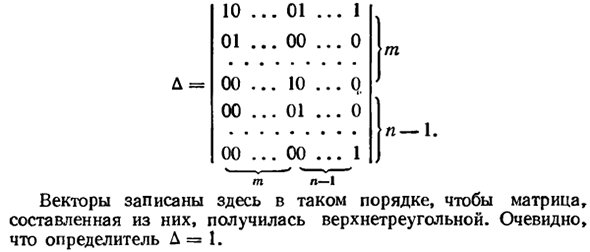
Чтобы доказать ранг системы Оно точно равно m + n — 1, и его достаточно найти в матрице A. Ненулевой второстепенный порядок m + ft-l. Вот так Например, несовершеннолетний Из первых m + n-1 компонент вектора A \ a, A ^ % 2 * …, A \ r- \ 94 110 01 00 00 00 … 01 .. … 00 .. … 10 .. … 01 .. … 00 .. , 1 , 0 • Q. , 0 , 1 м н — я Здесь вектор, матрица, Он состоял из них и оказался верхним треугольником. по-видимому Определитель Δ = K

Смотрите также:

Решение задач по ЭММ

Двойственный симплексный метод	Построение допустимых базисных решений транспортной задачи
Транспортная задача линейного программирования и методы ее решения	Основные теоремы теории двойственности