Оглавление:
Общий метод решения дробных неравенств
Один из самых общих методов решения дробных (не обязательно рациональных) неравенств состоит в сведении неравенства к равносильной ему совокупности двух систем, например:
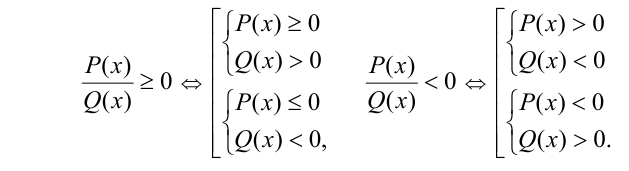
Заметим также, что
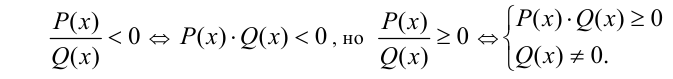
Если решаемое неравенство имеет вид
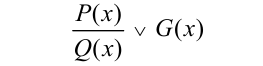
(знак  здесь заменяет любой из знаков неравенств), то, как правило, его следует привести к стандартному виду и уже затем решать:
здесь заменяет любой из знаков неравенств), то, как правило, его следует привести к стандартному виду и уже затем решать:
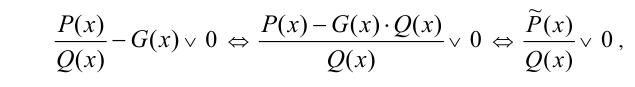
где 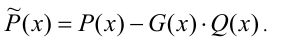
Пример №206.
Решить неравенство
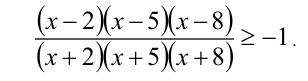
Решение:
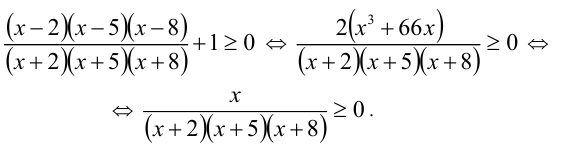
Далее неравенство решается методом интервалов (см. о методе интервалов далее).
Ответ: 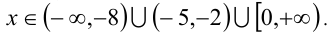
В следующем примере необходимо найти графический образ решения неравенства с двумя неизвестными на соответствующей координатной плоскости.
Пример №207.
На плоскости Оху изобразить множество точек (x;y) координаты которых удовлетворяют неравенству
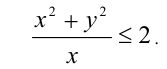
Решение:
Преобразуем неравенство:
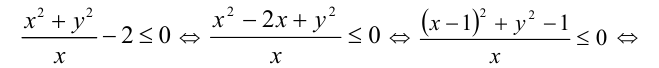
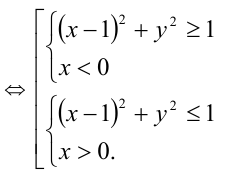
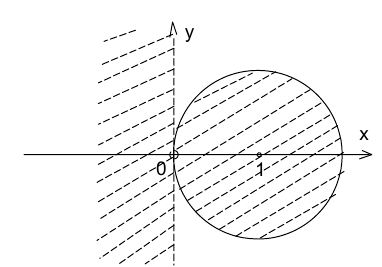
Графическим образом решений первой системы является пересечение внешней части круга единичного радиуса с центром в точке (1;0) и полуплоскости х < 0. Решение же второй системы на координатной плоскости представляет собой пересечение замкнутого круга единичного радиуса с центром в (1;0) и полуплоскости x > 0. Объединяя обе фигуры, получим окончательно ГМТ, изображённое на рисунке.
Замечание. Если в неравенстве вида
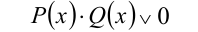
( P(x),Q(x) — любые функции, а знак v заменяет любой из знаков неравенства) один из сомножителей неотрицателен (неположителен) на ОДЗ, то обычно рассматривают два случая: 1) когда он равен нулю или 2) сохраняет постоянный знак. В первом случае все его корни проверяют, являются ли они решениями неравенства, а во втором случае на этот сомножитель делят обе части неравенства (с учётом знака), и получают в результате более простую задачу.
Пример №208.
Решить неравенство
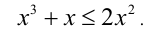
Решение:
Переписав неравенство в виде 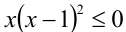 , заметим, что в левой его части содержится неотрицательный сомножитель
, заметим, что в левой его части содержится неотрицательный сомножитель 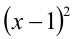 . Очевидно, x = 1 является решением. Чтобы найти оставшиеся (не равные единице!) решения, разделим неравенство на
. Очевидно, x = 1 является решением. Чтобы найти оставшиеся (не равные единице!) решения, разделим неравенство на 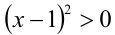 , и придём к неравенству
, и придём к неравенству 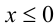 .
.
Ответ: 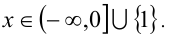
Пример №209.
Решить неравенство
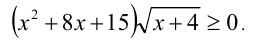
Решение:
ОДЗ: 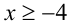 . Очевидно, что x = — 4 является решением данного неравенства. Найдём другие решения. Итак, пусть x > — 4, тогда поделив обе части неравенства на положительное выражение —
. Очевидно, что x = — 4 является решением данного неравенства. Найдём другие решения. Итак, пусть x > — 4, тогда поделив обе части неравенства на положительное выражение —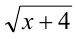 (с сохранением знака неравенства), придём к равносильному неравенству
(с сохранением знака неравенства), придём к равносильному неравенству
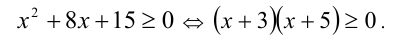
Решая последнее неравенство и учитывая ОДЗ, получаем 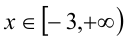 . Объединяя полученный промежуток с ранее найденным решением, приходим к ответу.
. Объединяя полученный промежуток с ранее найденным решением, приходим к ответу.
Ответ: 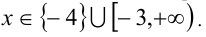
Пример №210.
Решить неравенство
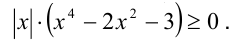
Решение:
Заметим, что x = 0 является решением неравенства. Чтобы найти ненулевые решения, поделим обе части на |х| (|х| > 0), и сведём, таким образом, задачу к решению биквадратного неравенства:
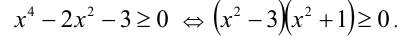
После сокращения на положительное выражение 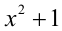 получаем неравенство
получаем неравенство 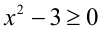 .
.
Ответ: 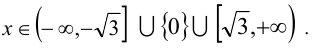
Пример №211.
Решить неравенство
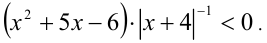
Решение:
ОДЗ: 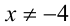 . Поскольку на ОДЗ сомножитель
. Поскольку на ОДЗ сомножитель 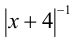 положителен, поделим на него обе части неравенства, получив равносильное неравенство
положителен, поделим на него обе части неравенства, получив равносильное неравенство 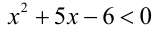 . Решением неравенства является интервал
. Решением неравенства является интервал 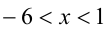 . С учётом ОДЗ получаем:
. С учётом ОДЗ получаем: 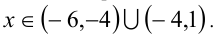
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

