Общие теоремы о равновесии системы материальных точек
Пусть связи, наложенные на систему материальных точек, допускают поступательное перемещение всей системы материальных точек вдоль некоторой неподвижной оси, которую всегда можно принять за ось х. Для этого возможного перемещения будем иметь
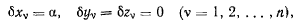
и тогда в соответствии с принципом Бернулли условие равновесия запишется в виде
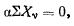
где а —отличный от нуля множитель. Отсюда следует, что необходимым условием равновесия является равенство нулю суммы проекций всех активных сил на ось х.
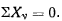
Предположим, что наложенные на систему связи допускают поворот всей системы, как одного целого, вокруг неподвижной оси. Примем эту ось за ось z. Скорости точек тела, вращающегося вокруг оси z, определяются известными формулами Эйлера
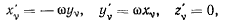
откуда для возможных перемещений получим
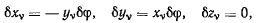
где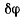 
угол поворота вокруг оси z. Подставляя эти значения в общее уравнение равновесия
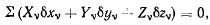
будем иметь
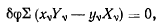
а условие равновесия получает вид
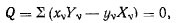
т. е. необходимым условием равновесия системы материальных, точек является равенство нулю суммы моментов всех активных, сил, действующих на систему, относительно оси z.
Рассмотрим равновесие твердого тела. Произвольное мгновенное перемещение твердого тела, как известно из кинематики,, сводится к мгновенно-винтовому перемещению. Пусть ось г — ось винтового перемещения твердого тела. Если обозначить через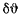 
бесконечно малый угол поворота твердого тела вокруг оси 2, а через 
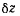величину поступательного перемещения твердого тела вдоль оси z, то для винтового перемещения будем иметь.
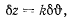
где k—параметр винта. Из общего уравнения статики
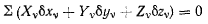
будем иметь
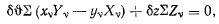
или
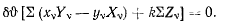
Обозначая через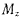 
— сумму моментов активных сил, действующих на твердое тело, относительно оси z, перепишем последнее уравнение в виде
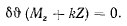
Отсюда следует, что для равновесия твердого тела необходимо выполнение условия
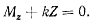
Замечание. Из того, что произвольное возможное перемещение твердого тела всегда может быть сведено к поступательному перемещению и к вращению вокруг некоторой оси, нетрудно сделать вывод, что в самом общем случае обобщенные силы имеют размерность силы или момента силы.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Связи и возможные перемещения |
| Обобщенные координаты |
| Метод неопределенных множителей Лагранжа |
| Определение реакций связи |
