Оглавление:
Общее уравнение линий второго порядка
Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям
Найдем сначала уравнение эллипса с центром в точке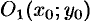 
оси симметрии которого параллельны координатным осям 
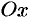и 
и 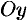полуоси соответственно равны 
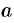и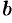 
. Поместим в центре эллипса 
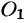начало новой системы координат 
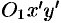, оси которо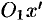й 
и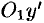 
параллельны соответствующим осям 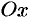и 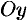и одинаково с ними направленны (см. рис. 63).
В этой системе координат уравнение эллипса имеет вид
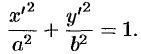
Так как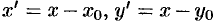 
(формулы параллельного переноса, см. с. 62), то в старой системе координат уравнение эллипса запишется в виде
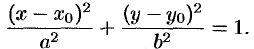
Аналогично рассуждая, получим уравнение гиперболы с центром в точке 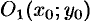и полуосям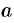и и 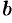(см. рис. 64):
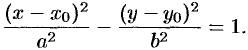
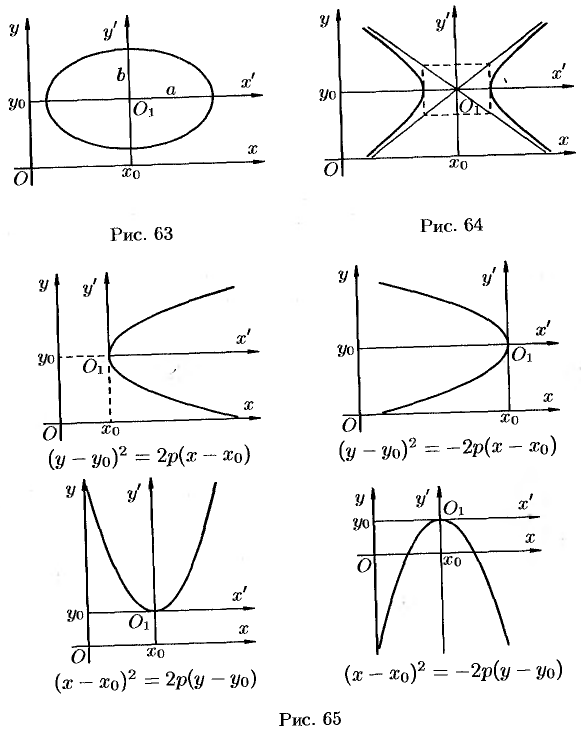
И, наконец, параболы, изображенные на рисунке 65, имеют соответствующие уравнения.
Уравнение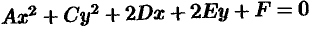 
Уравнения эллипса, гиперболы, параболы и уравнение окружности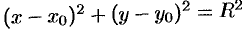 
после преобразований (раскрыть скобки, перенести все члены уравнения в одну сторону, привести подобные члены, ввести новые обозначения для коэффициентов) можно записать с помощью единого уравнения вида
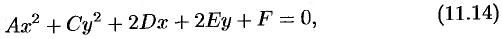
где коэффициенты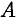 
и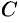 
не равны нулю одновременно.
Возникает вопрос: всякое ли уравнение вида (11.14) определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка? Ответ дает следующая теорема.
Теорема 11.2. Уравнение (11.14) всегда определяет: либо окружность (при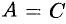 
), либо эллипс (при 
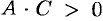), либо гиперболу (при 
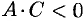), либо параболу (при 
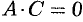). При этом возможны случаи вырождения: для эллипса (окружности) — в точку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся прямых, для параболы — в пару параллельных прямых.
Пример №11.1.
Установить вид кривой второго порядка, заданной уравнением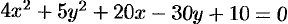 
.
Решение:
Предложенное уравнение определяет эллипс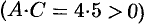 
. Действительно, проделаем следующие преобразования:
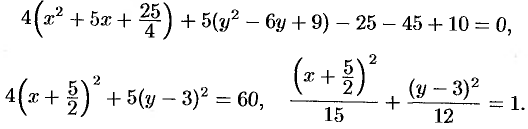
Получилось каноническое уравнение эллипса с центром в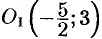 
и полуосям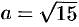и 
и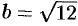 
.
Дополнительные примеры:
Общее уравнение второго порядка
Рассмотрим теперь общее уравнение второй степени с двумя неизвестными:
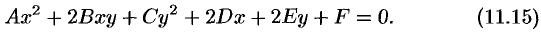
Оно отличается от уравнения (11.14) наличием члена с произведением координат (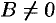
). Можно, путем поворота координатных осей на угол 
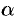, преобразовать это уравнение, чтобы в нем член с произведением координат отсутствовал.
Используя формулы поворота осей (с. 63)
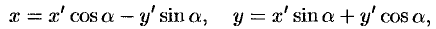
выразим старые координаты через новые:
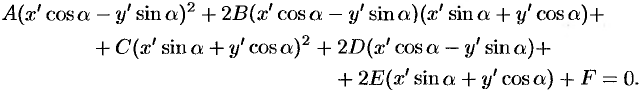
Выберем угол 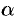так, чтобы коэффициент при 
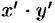обратился в нуль, т. е. чтобы выполнялось равенство
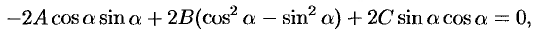
т. е.
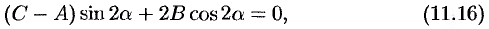
т. е.
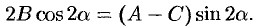
Отсюда
Таким образом, при повороте осей на угол 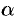, удовлетворяющий условию (11.17), уравнение (11.15) сводится к уравнению (11.14).
Вывод: общее уравнение второго порядка (11.15) определяет на плоскости (если не считать случаев вырождения и распадения) следующие кривые: окружность, эллипс, гиперболу, параболу.
Замечание: Если 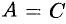, то уравнение (11.17) теряет смысл. В этом случае 
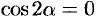(см. (11.16)), тогда 
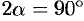, т. е. 
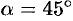. Итак, при 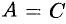систему координат следует повернуть на 
.
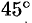На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Гипербола |
| Парабола |
| Плоскость. Основные задачи |
| Уравнения прямой в пространстве |
