Оглавление:
Общее уравнение динамики
Используя метод кинетостатики, мы можем условно приложить ко всем точкам движущейся системы силы инерции этих точек. Во всякий момент движения системы совокупность действующих на нее активных сил, реакций связей н условно приложенных сил инерции точек системы будет формально удовлетворять условию равновесия системы, выражаемому принципом возможных перемещении.
Согласно этому принципу при всяком возможном перемещении системы сумма элементарных работ всех приложенных к ней сил равна нулю.
Если наложенные связи на систему идеальные, то, как известно, сумма элементарных работ реакций таких связей при всяком возможном перемещении системы равна нулю. Таким образом, для системы с идеальными связями сумма
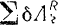
элементарных работ реакций связей из выражения для суммы элементарных работ всех приложенных сил выпадает, и мы получаем уравнение, носящее название общего уравнения динамики:
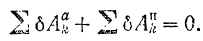
Во всякий момент движения системы с идеальными связями сумма элементарных работ всех прилоохенных к ней активных сил и сил инерции точек системы, условно приложенных к этим точкам, равна нулю на всяком возможном перемещении системы.
Пользуясь аналитическим выражением (189) элементарной работы, уравнению (217) можно придать и другую форму:
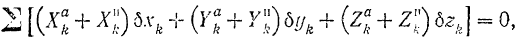
где 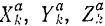 —проекции на оси координат приложенных к системе активных сил;
—проекции на оси координат приложенных к системе активных сил; 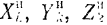 — проекции на оси координат сил инерции, условно приложенных к точкам системы;
— проекции на оси координат сил инерции, условно приложенных к точкам системы; 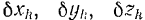 — приращения координат
— приращения координат 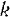 -й точки системы на возможном перемещении этой точки.
-й точки системы на возможном перемещении этой точки.
В случае, когда связи неидеальные и трением в них пренебречь нельзя, то, применяя общее уравнение динамики, надо включать силы трения в число активных сна, действующих на систему.
Приняв общее уравнение динамики за исходное, можно вывести из него все общие теоремы динамики. Оно как бы включает в себя всю механику, отчего и возникло его название.
Пример задачи:
Два шкива, соединенные бесконечным ремнем, вращаются вокруг неподвижных параллельных осей 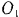 и
и 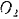 (рис. 245). Шкивы приводятся во вращение приводом, присоединенным к большему шкиву. Привод сообщает этому шкиву вращательный момент
(рис. 245). Шкивы приводятся во вращение приводом, присоединенным к большему шкиву. Привод сообщает этому шкиву вращательный момент 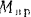 . Найти угловые ускорения шкивов и разность натяжении
. Найти угловые ускорения шкивов и разность натяжении 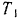 ведущего и
ведущего и 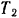 ведомого шкивов. Шкивы, веса которых
ведомого шкивов. Шкивы, веса которых 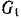 и
и 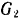 и радиусы
и радиусы 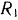 и
и 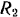 известны, считать сплошными однородными
известны, считать сплошными однородными
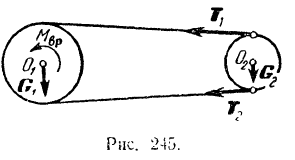
цилиндрами. Трением в осях, скольжением ремня и его пренебречь.
Решение:
Присоединим к активным силам, действующим на систему (шкивы — ремень), силы инерции шкивов и дадим ведущему шкиву возможное перемещение — поворот на бесконечно малый угол 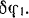 .
.
Соответствующее перемещение ведомого шкива находится из соотношения
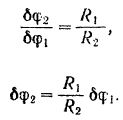
В аналогичной зависимости находятся и угловые ускорения шкивов:
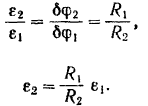
Составляем общее уравнение (217) динамики:
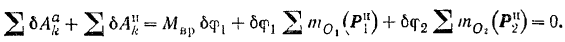
По формуле (212) сумма моментов сил инерции точек ведущего шкива относительно его оси 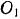 вращения:
вращения:
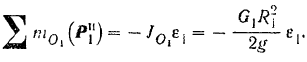
По той же формуле, сумма моментов сил инерции точек ведомого шкива относительно его оси 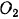 вращения:
вращения:
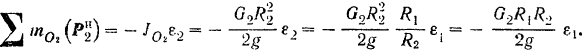
Подставляя соответствующие значения в общее уравнение динамики, будем иметь:
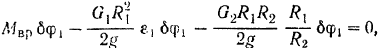
откуда находим угловое ускорение ведущего шкива
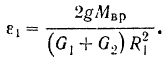
Угловое ускорение ведомого шкива
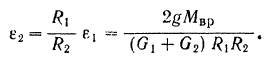
Для того чтобы определить разность  натяжений ремни (рис. 245) составим основное уравнение (182) динамики для вращательного движения ведомого шкива:
натяжений ремни (рис. 245) составим основное уравнение (182) динамики для вращательного движения ведомого шкива:
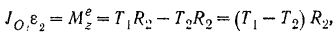
откуда искомая разность натяжений ремня:
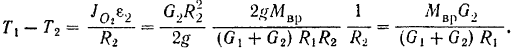
Пример задачи:
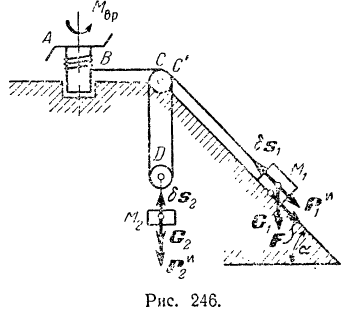
Вал кабестана (вертикального ворота) радиуса 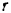 приводится во вращение постоянным вращающим моментом
приводится во вращение постоянным вращающим моментом 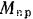 , приложенным к рукоятке
, приложенным к рукоятке 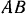 (рис. 246). Трос, наматываемый на вал кабестана при его вращении, идет через неподвижный блок
(рис. 246). Трос, наматываемый на вал кабестана при его вращении, идет через неподвижный блок 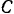 , затем, охватывая подвижный блок
, затем, охватывая подвижный блок 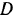 , возвращается на неподвижный блок
, возвращается на неподвижный блок 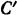 , надетый на ту же ось, что и блок
, надетый на ту же ось, что и блок 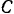 , и проходит параллельно наклонной плоскости, где к концу троса привязан груз
, и проходит параллельно наклонной плоскости, где к концу троса привязан груз 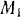 весом
весом 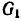 . Коэффициент трения груза
. Коэффициент трения груза 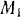 о наклонною плоскость составлявшую с горизонтом угол
о наклонною плоскость составлявшую с горизонтом угол  равен
равен 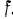 . Подвижный блок
. Подвижный блок 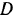 несет груз
несет груз 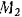 весом
весом 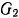 . Пренебрегая массами кабестана определить ускорение грузов.
. Пренебрегая массами кабестана определить ускорение грузов.
Решение:
Отнесем к активным силам, действующим на данную систему, силу трения 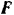 груза о наклонную плоскость и проведенным к ним силы
груза о наклонную плоскость и проведенным к ним силы 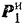 и
и 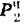 инерции грузов
инерции грузов 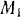 и
и 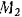 . Сила трения груза
. Сила трения груза 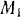 равна
равна
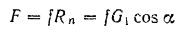
и направлена вдоль наклонной плоскости вниз. Сила инерции груза 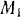 равна
равна
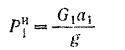
и направлена вдоль наклонной плоскости вниз. Сила инерции груза 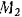 равна
равна
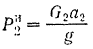
и направлена вертикально вниз.
Дадим валу кабестана возможное перемещение — поворот на элементарный угол 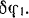 . Этому перемещению будет способствовать перемещение груза
. Этому перемещению будет способствовать перемещение груза 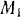
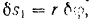
где 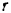 — радиус вала кабестана. Соответствующее перемещение груза
— радиус вала кабестана. Соответствующее перемещение груза 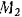 будет равно
будет равно
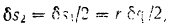
так как подвижный блок висит на двух ветках троса.
Ускорения грузов 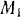 и
и 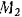 пропорциональны их перемещениям
пропорциональны их перемещениям
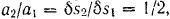
откуда
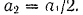
Составляя общее уравнение динамики, будем иметь:
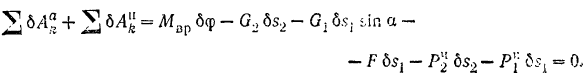
Выражая в последнем равенстве все перемещения через 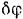 и ускорение
и ускорение 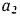 через ускорение
через ускорение 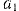 , получим:
, получим:
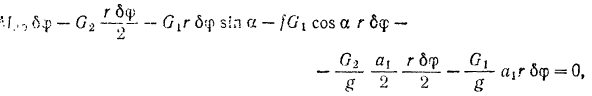
откуда ускорение груза 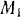 будет равно
будет равно
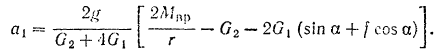
Легко находится теперь и ускорение груза 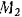 :
:
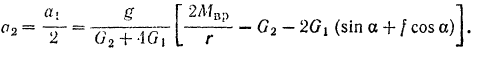
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

