Оглавление:
Обратное преобразование Лапласа
Теоремы разложения
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению 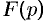 находить соответствующий ему оригинал
находить соответствующий ему оригинал 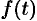 .
.
Теорема 79.1. Если функция 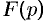 в окрестности точки
в окрестности точки 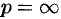 может быть представлена в виде ряда Лорана
может быть представлена в виде ряда Лорана
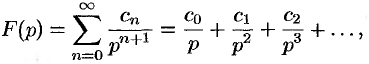
то функция
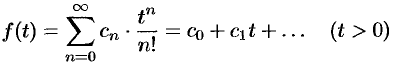
является оригиналом, имеющим изображение 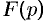 , т. е.
, т. е.
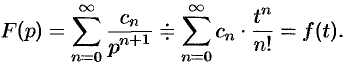
Примем эту теорему без доказательства.
Пример №79.1.
Найти оригинал 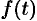 , если
, если
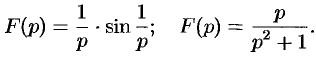
Решение:
Имеем
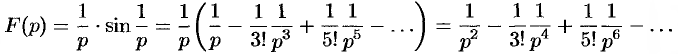
Следовательно, на основании теоремы 79.1 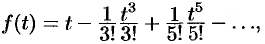
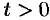 .
.
Запишем лорановское разложение функции 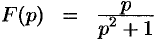 в окрестности точки
в окрестности точки 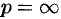 :
:
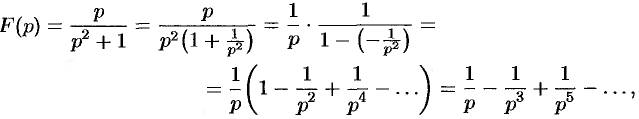
где 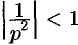 , т. е.
, т. е. 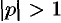 . Следовательно,
. Следовательно, 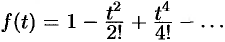 , т. е.
, т. е. 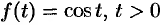 .
.
Теорема 79.2. Если 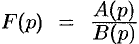 правильная рациональная дробь, знаменатель которой
правильная рациональная дробь, знаменатель которой 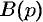 имеет лишь простые корни (нули)
имеет лишь простые корни (нули) 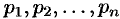 , то функция
, то функция
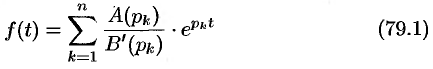
является оригиналом, имеющим изображение 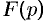 .
.
Отметим, что дробь 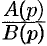 должна быть правильной (степень многочлена
должна быть правильной (степень многочлена 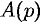 ниже степени многочлена
ниже степени многочлена 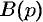 ); в противном случае не выполняется необходимый признак существования изображения
); в противном случае не выполняется необходимый признак существования изображения 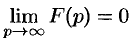 (п. 78.1), т. е.
(п. 78.1), т. е. 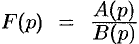 не может быть изображением.
не может быть изображением.
Разложим правильную рациональную дробь 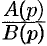 на простейшие:
на простейшие:
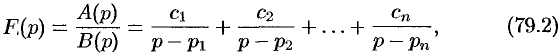
где 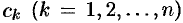 — неопределенные коэффициенты. Для определения коэффициента
— неопределенные коэффициенты. Для определения коэффициента 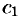 этого разложения умножим обе части этого равенства почленно на
этого разложения умножим обе части этого равенства почленно на 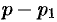 :
:
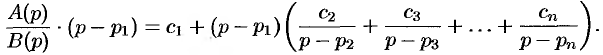
Переходя в этом равенстве к пределу при 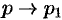 , получаем
, получаем
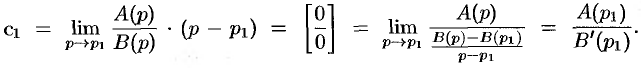
Итак, 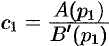 . Аналогичным путем (умножая обе части равенства (79.2) на
. Аналогичным путем (умножая обе части равенства (79.2) на 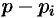 ) найдем
) найдем 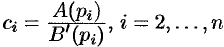 .
.
Подставляя найденные значения 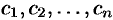 в равенство (79.2), получим
в равенство (79.2), получим
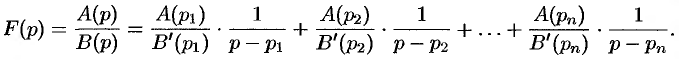
Так как по формуле (78.3)
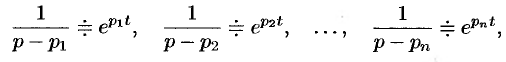
то на основании свойства линейности имеем
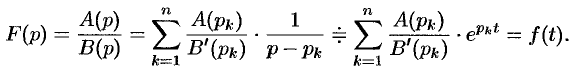
Замечание. Легко заметить., что коэффициенты 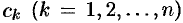 определяются как вычеты комплексной функции
определяются как вычеты комплексной функции 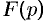 в простых полюсах (формула (77.4)):
в простых полюсах (формула (77.4)): 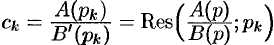 .
.
Можно показать, что если 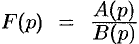 — правильная дробь, но корни (нули)
— правильная дробь, но корни (нули) 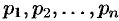 знаменателя
знаменателя 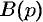 имеют кратности
имеют кратности 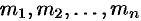 соответственно, то в этом случае оригинал изображения
соответственно, то в этом случае оригинал изображения 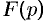 определяется формулой
определяется формулой
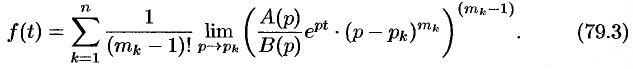
Теорему 79.2 можно сформулировать следующим образом:
Теорема 79.3. Если изображение 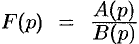 является дробно-рациональной функцией от
является дробно-рациональной функцией от 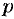 и
и 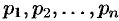 — простые или кратные полюсы этой функции, то оригинал
— простые или кратные полюсы этой функции, то оригинал 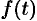 , соответствующий изображению
, соответствующий изображению 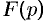 , определяется формулой
, определяется формулой
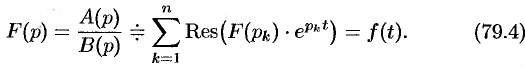
Формула Римана-Меллина
Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид
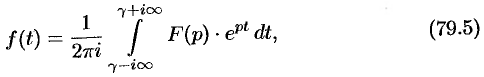
где интеграл берется вдоль любой прямой 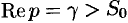 .
.
При определенных условиях интеграл (79.5) вычисляется по формуле
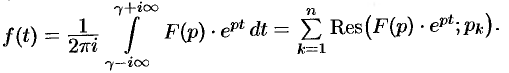
Замечание. На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения 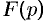 соответствующий ему оригинал; второй путь состоит в том, что функцию
соответствующий ему оригинал; второй путь состоит в том, что функцию 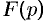 стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
Пример №79.2.
Найти оригинал по его изображению 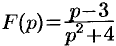 .
.
Решение:
Проще всего поступить так:
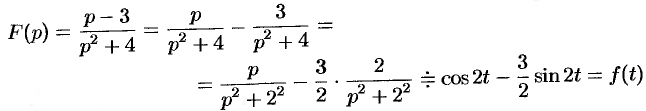
(использовали свойство линейности и формулы (78.5) и (78.6)).
Если же использовать теорему 79.2 разложения, то будем иметь: 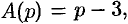
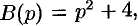
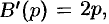 корни знаменателя
корни знаменателя 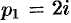 и
и 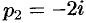 и, согласно формуле (79.1),
и, согласно формуле (79.1),
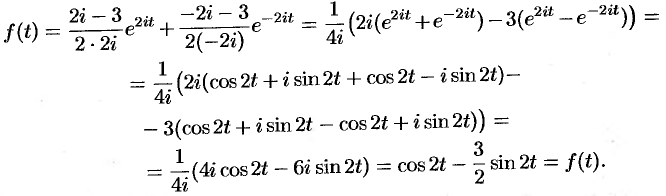
Пример №79.3.
Найти функцию-оригинал, если ее изображение задано как 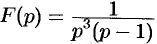 .
.
Решение:
Здесь 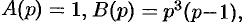
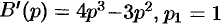 — простой корень знаменателя,
— простой корень знаменателя, 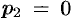 — 3-кратный корень (
— 3-кратный корень (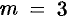 ). Используя формулы (79.1) и (79.3), имеем:
). Используя формулы (79.1) и (79.3), имеем:
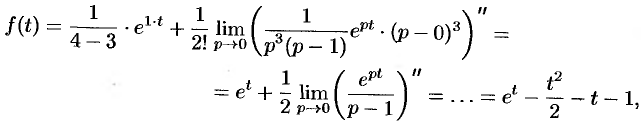
т. е. 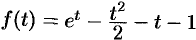 .
.
Приведем другой способ нахождения 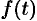 . Разобьем дробь
. Разобьем дробь 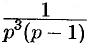 на сумму простейших дробей:
на сумму простейших дробей: 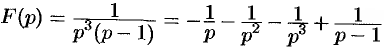 . Следовательно,
. Следовательно, 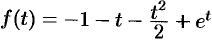 .
.
Приведем третий способ нахождения 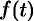 . Представим
. Представим 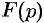 как произведение
как произведение 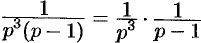 , и так как
, и так как 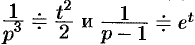 , то, пользуясь свойством умножения изображений, имеем:
, то, пользуясь свойством умножения изображений, имеем:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Вычисление вычетов. Применение вычетов в вычислении интегралов |
| Свойства преобразования Лапласа |
| Действия над матрицами |
| Элементарные преобразования матриц |

