Обратная задача. Определение центральной силы, когда задана траектория

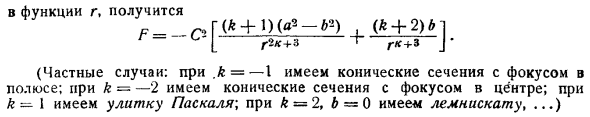
Обратная задача. Определение центральной силы, когда задана траектория

• Поставьте следующую задачу. Точки представляют собой плоские траектории в соответствии с законом площади для фиксированного центра. Найдите силу, которая вызывает это движение. Прежде всего, эта сила является center. Фактически, фиксированная точка является отправной точкой. И тогда, согласно законам предметной области, возникает уравнение. Оттуда, дифференциация, мы получаем dt. Это уравнение показывает, что ускорение, а следовательно, и сила, всегда проходит через начальную точку. Пусть F алгебраическое значение силы. Тогда на основе равенства 6. По предположению, уравнение локуса f r, b = 0 известно и определяет y функции 0:y = 0. И так оно и есть.

Действительно, если система не находится в равновесии и предоставлена самой себе, то она начнет двигаться. Людмила Фирмаль

Если заранее нет никаких ограничений на природу силы F, то задача остается неясной, так как изгиб связан заданной equation. As в результате уравнение F может быть преобразовано бесчисленными способами, и обычно только функция r должна выражать F в предыдущем уравнении и ту, которая должна исключить 0 из уравнения траектории. Образцы. 1.Рассмотрим случай конического сечения, которое описывается законом площади, связанной с фокусом, и направлено на этот фокус вогнутой поверхностью.

• Сосредоточившись на полюсах, находим уравнение сечения конуса День 1 0, где P параметр, А E эксцентриситет. Я найду его здесь. Таким образом, сила притяжения изменяется обратно пропорционально 2 м квадратам расстояния. 2.Учитывая ту же задачу о ветви гиперболы, которая выпукла к фокусу, уравнение 1 e потому 6 1 7 П И затем… т. rg Таким образом, мы получаем тот же закон для силы, но с отталкиванием. 3.Большинство кривых, которые возникают с такими проблемами, включены в уравнение РК = а потому Джей Где a, b, k константы.

Если для всех перемещений, допускаемых связями, сумма сГо работ заданных сил равна нулю, то система находится в равновесии. Людмила Фирмаль

Предполагая, что эти кривые описываются по закону области относительно начальной точки, можно сказать, что для силы, представленной функцией r , +2 6 Л Г2 + с 1г + с г Особый случай: к = у меня конус раздел ориентирован на поляков к = 2 имеет коническую секцию сосредоточена в центре к 1 имеет Паскаля улитка, и K = 2, 6 = 0 имеет lemnis коньки. Результирующий вектор будет равен этой сумме и связан с центром заданной системы параллельных связанных векторов. Рп, причем порядок однородности равен нулю. В этом случае точка С не существует. Эти векторы в общем случае образуют пару, если только они не прямо противоположны. параллельных связанных векторов относительно плоскости.

Смотрите также:

Решение задач по теоретической механике

Уравнения движения	Следствия из законов Кеплера
Сила есть функция только расстояния	Кометы